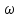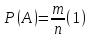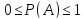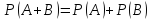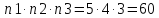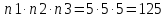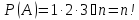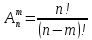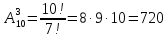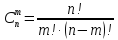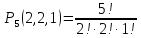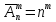Событий какого вида из перечисленных не существует с точки зрения теории вероятностей

Виды вероятностей. Теоремы сложения

1. Услуги проектирования
2. Теория вероятности [Калинин В.М., Тихомиров С.Р.]
3. Виды вероятностей. Теоремы сложения

Геометрическая вероятность

Чтобы преодолеть ограниченность классического определения вероятности неприменимого к испытаниям с бесконечным числом исходов вводят геометрическую вероятность- вероятность попадания точки в область.

для лини $P=\frac $ для площади $P=\frac $

Пример. На плоскости начерчены две концентрические окружности радиуса $R_1 =5$ и $R_2 =10$. Найти вероятность попадания точки в кольцо.

Решение: Площадь кольца $S=\pi ( )=\pi ( )$

Площадь большого круга $S=100\,\pi $

Теоремы сложения вероятностей

Теорема 1 Если события А и В — несовместны, то \begin \label P( )=P( A )+P( B ) \qquad (1) \end

Пример: Вероятность выхода изделия из строя при эксплуатации сроком до одного года равна 0,1, а при эксплуатации сроком до пяти лет — 0,3. Найти вероятность выхода изделия из строя при эксплуатации сроком от одного года до пяти лет.

Решение. Введем события:

Так как $A$ и $B$ — несовместные события , то событие $C=A+B$. Из теоремы сложения несовместных событий — $ P(C)=P(A+B)=P(A)+P(B) $ найдем вероятность выхода изделия из строя при эксплуатации сроком от одного года до пяти лет. $ P(B)=P(C)-P(A)=0,3-0,1=0,2. $

Теорема 2 Сумма вероятностей противоположных событий равняется единице

Следствие Вероятность полной группы несовместных событий $P( )+P( )+\ldots +P( )=1$(3)

Опр. Случайные события A и B называются совместными, если при испытании могут произойти оба события т.е. произойдет совмещение событий.

Теорема 3 Вероятность суммы совместных событий равна \begin \label P( )=P( A )+P( B )-P( ) \qquad (2) \end

Пример: Отдел технического контроля проверяет на стандартность по двум параметрам серию изделий. Было выявлено, что у 8 из 25 изделий не выдержан только первый параметр, у 6 изделий — только второй, а у 3 изделий не выдержаны оба параметра. Наудачу берется одно из изделий. Какова вероятность того, что оно не удовлетворяет стандарту?

Решение. Введем события:

Событию $A$ благоприятствуют $8+3=11$ исходов. Вероятность наступления события $A$ можно найти по формуле классической вероятности $P(A)=\frac $. Событию $B$ благоприятствуют $6+3=9$ исходов. Вероятность наступления события $B$ можно найти по формуле классической вероятности $P(B)=\frac $. Событию $( )$, состоящему в том, что у взятой детали не выдержаны оба параметра, благоприятствуют $3$ исхода. Вероятность наступления события $( )$ можно найти по формуле классической вероятности $P(A\cdot B)=\frac $. Наступление события $C$ означает, что у взятого наудачу изделия либо не выдержан первый параметр, либо второй, либо оба вместе, т.е. $C=A+B$. Число нестандартных изделий равно $8+6+3=17$. События $A$ и $B$- совместны , тогда вероятность наступления события $C$ можно найти по формуле

Условная вероятность

Опр. Событие $A$ называется зависимым от события $B$, если вероятность появления события А зависит от того произошло событие В или нет?

Опр. Условной вероятностью $P_B ( A )$или $P( )$ называется вероятность появления события $A$ при условии, что событие В уже произошло.

Пример: В урне 3-и белых и 3-и черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара , если при первом испытании был извлечен черный шар .

Решение. Всего в урне 6-ть шаров. После первого испытания в урне осталось 5-ть шаров из них 3-и белых. Вероятность вытащить белый шар , при условии, что 1-м был черный есть .

Теорема Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого $\begin \label P( )=P_B ( A )\cdot P( B ) \qquad (3) \end $

Следствие Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности остальных $ P( )=P( )\cdot P_ ( )\cdot P_ ( )\cdot \ldots \cdot P_ > ( ) $

Например: для трех событий $ P( )=P( A )\cdot P_A ( B )\cdot P_ ( C ) $

Пример: В коробке девять одинаковых радиоламп, три из которых были в употреблении. В течение рабочего дня мастеру для ремонта аппаратуры пришлось взять две радиолампы. Какова вероятность того, что обе взятые лампы были в употреблении?

Решение. Введем события:

Событие $C=A\cdot B$. Вероятность того, что первая взятая радиолампа была в употреблении, подсчитаем по формуле классической вероятности: m — благоприятные события — три лампы были в употреблении, n -всевозможные события — всего ламп в коробке девять $P(A)=\frac =\frac $. После того как произошло событие $A$, в коробке осталось восемь ламп из которых две были в употреблении. Событие $B$ наступает только при условии, что событие $A$ наступило, поэтому для нахождения вероятности события $B$, состоящего в появлении второй раз радиолампы, бывшей в употреблении используем условную вероятность $P_A (B)=\frac $. Следовательно, вероятность появления двух таких ламп может быть найдена по теореме о вероятности произведения зависимых событий — по формуле $ P(C)=P(A\cdot B)=P(A)\cdot P_A (B)=\frac \cdot \frac =\frac . $

Замечание. Из формулы получим формулу для условной вероятности $\begin \label P_B ( A )=\frac ) > \qquad (4) \end $

Вычисление площади поверхности

Определение тройного интеграла. Теорема существования тройного интеграла

СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице

Введение

Вычисление двойного интеграла

Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Теорема о заведомо полныx системаx

Полином Жегалкина. Пример.

Критерий полноты . Лемма о несамодвойственной функции

Несобственные интегралы по неограниченной области

Теорема Стокса

Нормальные формы

Специальные векторные поля

Вычисление площадей плоских областей

Вычисление криволинейного интеграла второго рода. Примеры.

Огравление $\Rightarrow $

1.Предмет теории вероятности. Виды событий. Действия над событиями.

Любая точная наука изучает не сами явления и процессы, а их математические модели.

Существуют задачи, когда совокупное влияние случайных факторов придающих конкретному опыту существенное влияние превышают или сравнимы с действиями основных факторов, выявленные в задачах с закономерностями, называют вероятностными или статистическими.

Теория вероятности – математическая наука, изучающая закономерности массовых случайных явлений.

Предметом теории вероятности является математические модели случайных явлений.

Под случайным явлением понимается явление, исход которого заранее предсказать нельзя.

Цель теории вероятности – осуществление прогноза в области случайных явлений, их контроль и т.п.

Результаты любого опыта можно характеризовать качественно и количественно.

Качественной характеристикой результата является событие.

События принято делить на достоверные, невозможные и случайные.

Достоверное — событие, которое обязательно произойдет при выполнении определенного комплекса условий.

Пример: «Тяжелый шарик на наклонной плоскости покатится обязательно в сторону»

Невозможное – событие, которое обязательно не произойдет при выполнении определенного комплекса условий.

Пример: «Из герметично закрытого сосуда вода не может вылиться».

Случайное – событие, которое при определенном комплексе условий, либо произойдет, либо не произойдет.

Пример: «Уроненная на пол чашка, либо разобьется, либо останется на поврежденной»

События называются несовместными, если появление в 1-ом и тот же испытании 1-ого из них полностью исключает появление других событий.

Пример: «Попадание и промах при выстреле по цели»

В противном случае – события называются совместными.

Несколько событий образуют полную группу, если появление 1-ого из них является достоверным событием.

Несколько событий называют равновозможными, если при проведении опыта могут произойти несколько событий и каждое из них не является более возможным, чем другое.

Основные операции проводятся аналогично основным операциям над множествами.

Сумма А и В называется событие С=А+В, состоящее в появлении событий А и В вместе.

Произведение А и В называется событие С=А*В, состоящее в появлении событий А и В одновременно.

Противоположное событие А происходит тогда и только тогда, когда событие А не происходит.

Разностью событий А и В называется событие С=А-В, означающее, что событие А-происходит, В – не происходит.

Множество всех элементарных событий обозначается омегой.

Достаточное событие-

Невозможное-.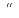

2. Свойство статистической устойчивости относительной частоты событий. Статистическое определение вероятности.

Пусть в «n» повторяющихся опытах некоторое событие А наступилоn_А раз.

Число n_A называетсячастотой события А в рассматриваемой серии опытов.

Отношение n_A/n=P*(A) называетсяотносительной частотой(частотностью)события А.

(1.1)

Относительная частота события обладает следующими свойствами:

Частота любого события заключается между 0 и 1.

Частота невозможного события равна 0.

Частота достоверного события равна 1.

Частота суммы двух несовместных событий равна сумме частот этих событий.

Частота обладает еще одним свойством – свойством статистической устойчивости– с увеличением числа опытовn, она принимает значения близкие к некоторому постоянному числу. В этом случае говорят, что частота стабилизируется, приближаясь к некоторому числу.

В опыте бросания монеты относительная частота появления герба при 4040 бросаний оказалась равна 0,5096 = 2048/4040. При 12000 и 24000 она оказалась соответственно равна 6018/12000 = 0,5015 и 12012/24000 = 0,5005. Таки образом частота приближается к числу 0,5.

Отметим, что теория вероятности изучает только те массовые случайные явления с неопределенным исходом, для которых предполагается наличие устойчивой относительной частоты.

Количественной характеристикой события является Вероятность события, т.е. число, выражающее степень возможности его появления в данном опыте. Существует несколько математических определений вероятности, дополняющих и обобщающих друг друга.

Рассмотрим определение, в основе которого лежит выражение (1.1)

Статистическая вероятность– число, около которого колеблется относительная частота события А при достаточно большом числе опытов.

(1.2)

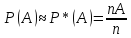
Вероятности Р(А) приписывают свойства 1-4 относительной частоты.

Классическое определение вероятности. Свойство вероятностей. Элементы комбинаторики.

Пусть проводится опыт с n исходами, которые можно представить в виде полной группы несовместных равновозможных событий, называемых элементарным событием.

Элементарное событие, приводящее к появлению событию A, называется благоприятным, или благоприятсвующими событию А.

Вероятность события A называется отношение m – элементарное событие, благоприятсвующее к событию А, к общему числу n – равновозможные несовместных элементов событий, образу.щих полную группу.

Из данного определения выполняются свойства вероятности (P):

вероятность достоверного события

вероятность невозможного события

вероятность случайного события

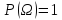
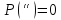
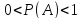
Вероятность суммы несовместных событий

Вероятность суммы противоположных событий = 1

Расчет вероятностей обычно производится по формулам комбинаторики.

Комбинаторика – это раздел математики, в котором изучаются задачи выбора элемента из заданного множества и расположения их в группы по определенным правилам.

Многие комбинаторные задачи решаются с помощью двух правил: умножения и сложения.

Правило умножения: Если из некоторого известного количества конечного множества первый объект (элемент Х) можно выбрать n1 способами и после каждого (элемента Y) n2 способами, то оба объекта X и Y можно выбрать в указанном порядке n1*n2 способами.

Пример 1: Сколько 3-х значных чисел можно составить из цифр 1,2,3,4,5, если:

цифры не повторяются

Цифры могут повторяться

Для выбора 1 цифра имеется 5 вариантов (n1=5), для выбора 2-ой цифры — 4 варианта (n2=4), для выбора 3-ой цифры (n3=3)

Для выбора 1-ой цифры (n1=5), для выбора 2-ой цифры (n2=5), для выбора 3-ой цифры (n3=5)

Если некоторый объект Х можно выбрать n1 способами, а второй объект Y n2 способами, при чем 1-ый и 2-ый способны пересекаться, то любой из указанных объектов логично выбрать n1+n2 способами.

Пример 2: В студенческой группе 15 девушек и 10 юношей, сколькими способами можно выбрать двух студентов одного пола.

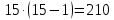
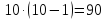
По правилу умножения двух девушек можно выбрать: девушекюношей

Существуют две схемы выбора m элементов 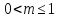из исходного множества:

без возвращения (без повторений)

с возвращениями (с повторения)

Схемы выбора без возвращения. Схемы выбора с возвращением.

Рассмотрим схемы без возвращения. Пусть дано множество из n различных компонентов. Перестановками из n различных элементов и отличающимися полным порядком расположения

Размещение из n элементов по m элементам называется комбинацией по m элементам и отличающиеся друг от друга либо порядком расположения элемента, либо элементами.

Пример 3: Сколько комбинаций, отличающихся элементами и их расположением, из 10 цифр по 3.

Сочетаниями из n элементов по m элементам называется комбинации по m элементам и отличающихся друг от друга хотя бы одним знаком.

Пример 4: Сколько комбинаций можно составить из 10 частей по 3 отличающихся хотя бы одним числом.

Схема выбора с возвратом.

Пусть в множестве с n элементами есть k различных элементов, при чем 1-ый элемент повторяется n1 раз, 2-ой – n2 … k-ый – nk раз, причем n=n1+n2+…+nk.

Перестановками из n элементов данного множества называют перестановками с повторениями (с возвращениями) из n элементов, число которых вычисляется по формуле:

Пример 5: Сколько различных 5-значныз чисел можно составить из: 3,3,7,7,9

Если при выборе m элементов из n элементов возвращаются обратно и упорядываются, то говорят, что это размещение с повторением.

Размещение с повторением могут отличаться друг от друга элементами, их порядком и количеством. Число таких размещений.

Пример 6: Сколько 5-значных чисел можно составить из цифр 2,3,7,9:

Если при выборке m элементов из n элементов возвращаются, но не упорядываются, то говорят, что это сочетание с повторением:

Пример 7: Сколькими способами можно составить букет из 5 цветов, если в наличие есть цветы трех сортов.

Условия вероятности. Вероятность произведения событий.

Пусть А и В-события, рассматриваемые в данном опыте. Наступление одного из этих событий (А) может повлиять на появление одного из другого события (В). Для характеристики зависимости одного события из другого вводят понятие условной вероятности.

Условной вероятностью события (В) при условии, что событие (А)ужепроизошло называется отношение вероятности произведения событий А и В к вероятности события (А):

Вероятность Р(А)в отличии от условной вероятности наз.безусловной вероятностью.

Аналогично, вероятность события (А) при условии, что событие (В) уже произошло определяют формулой:

ПРИМЕР: В урне3белых и7черных шаров. Из них вытаскивают2шара. Какова вероятность того, что 2ой шар будет белый, при условии, что 1ый есть черный.

В – 2ой шар белый

Вероятность произведений 2х событий равна произведению безусловной вероятности одного из событий на условную вероятность 2ого события, при условии, что 1ое произошло.

Правило условности имеет более простой вид, если рассматривать события независимыми, т. е. условная вероятность события равна его безусловной вероятности.

Р(АВ) = Р(А)*Р(В) или для случая nнезависимых событий имеет вид:

Из свойств вероятности известно, что вероятность суммы 2х несовместных событий равна сумме их вероятностей:

Вероятность суммы 2х совм. событий опр. выражение:

Для 3х событий А, В, С: Р(А+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС)

В

АВС

Формула полной вероятности.

Одним из следствий совместного применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса.

События А₁,А₂…,А_nобразуют полную группу, если А_i*Аj≠ɸ, i≠j и 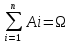. Систему таких событий называют разбиением

Пусть события Н₁,Н₂,…Н_n образуют полную группу. Тогда для любого, наблюдаемого в опыте события А имеет место формула полной вероятности.

Т.к. Н₁+Н₂+…+Н_n=Ω, то в силу свойств операций над событиями А=А*Ω=А*(Н₁+Н₂+…+Н_n)=А* Н₁+А* Н₂+…+ А* Н_n. Из того, что Н_i*Н_j=ɸ следует, что (А*Н_i)*(А* Н_j)= ɸ, i≠j, т.е. события А*Н_i и А* Н_j также несовместны. Тогда по теореме сложения вероятностей Р(А* Н₁)+Р(А* Н₂)+…+Р(А* Н_n) т.е. Р(А)=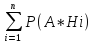. По теореме умножения вероятностей Р(А*Н_i)= P(A∣Н_i)*P(Н_i).

События Н₁,Н₂…Н_n обычно называют гипотезами, они исчерпывают все возможные предположения(гипотезы) относительно исходов как бы первого этапа опыта, события А-один из возможных исходов второго этапа. ЖОПА.

Пример: В сборочный цех поступает 40% деталей из цеха 1 и 60% из 2 цеха. В 1 цехе производится 90% стандартных деталей, а во 2-95%. Найти вероятность того, что взятая на удачу сборщиком деталь окажется стандартной.

Решение: Взятие детали можно разбить на два этапа. Первый- выбор цеха. Имеется две гипотезы:Н₁-деталь изготовлена цехом 1, Н₂-2 цехом. Второй этап взятие детали. Событие А-взятая наудачу деталь стандартна. Очевидно, события Н₁,Н₂образуют полную группу, Р(Н1)=0,4, Р(Н2)=0,6. Числа 0,90 и 0,95 являются условными вероятностями события А при условии гипотез Н1 и Н2 соответственно, т.е. Р(А|Н₁)=0,90 и Р(А|Н₂)=0,95. По формуле полной вероятности находим Р(А)=

Следствием формулы полной вероятности является формула Байеса или теорема гипотез. Она позволяет переоценить вероятности гипотез Н_i, принятых до опыта и называемых априорными по результатам уже проведенного опыта, т.е. найти условные вероятности Р(Н_i|A), которые называют ЖОПА апостериорными (после опыта)

Теорема: Пусть события Н₁,Н₂,…Н_n образуют полную группу. Тогда условная вероятность события Н_k(k=1,n) при условии, что событие А произошло, задается формулой

Определим вероятность гипотезы Н₂при условии, что событие А (взятая деталь стандартна) уже произошло, т.е. Р(Н₂|А):

События, виды событий

Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Примеры испытаний: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесённой на каждую из шести граней цифры от одного до шести), реализация некоторого физического, механического или технологического процесса и т.д. При бросании монеты исходами (событиями) являются выпадение герба или выпадение цифры, а при бросании игральной кости — выпадение какой либо цифры на верхней грани кости. Испытания сопровождаются их исходами (событиями).

Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д.

Различают следующие типы событий: случайные события, совместные или несовместные события, достоверные или невозможные события, зависимые или независимые события, равновозможные события, элементарные (простые, неразложимые) события, событие или совокупность событий (исходов), благоприятствующих какому-либо другому событию.

Случайное событие – это результат испытания (или величина), который нельзя заранее спрогнозировать, т.е. нельзя сказать, произойдёт это событие или не произойдёт, или, если событие произойдёт, то неизвестно, какое значение примет результат этого события.

Случайные события – первичные, неопределяемые (в строгом смысле) понятия в теории вероятностей, аналогичные понятиям точки и прямой – в геометрии.

Например, пусть игральная кость с пронумерованными гранями от 1 до 6 подбрасывается два раза. В этом опыте можно рассматривать следующие события: событие А – оба раза выпадет число 1; событие В – хотя бы один раз выпадет число 3; событие С – сумма выпавших чисел равна 8 и т.д.

Событие, которое обязательно наступит (никогда не произойдёт) в данном опыте, называется достоверным (невозможным). Достоверное событие обозначают символом Ω, а невозможное – Æ. Например, в опыте, состоящем в подбрасывании кости один раз – событие А – выпадение одного из чисел 1,2,3,4,5,6 – есть достоверное, а событие В – выпадение числа 7 – невозможное.

Два случайных события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же испытании. (Таким образом, несовместные события не могут наступать одновременно). В противном случае, т.е. если наступление одного события не исключает наступление другого события в одном и том же испытании, то эти события называются совместными. Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.

События А₁, А₂, … , А_n называются попарно несовместными, если любые два из них являются несовместными.

События называются равновозможными, если ни одно из них не является более возможным по сравнению с другими событиями.

События называются независимыми (зависимыми), если числовая характеристика возможности наступления одного события не зависит (зависит) от числовых характеристик наступления других событий (указанные числовые характеристики некоторых событий А, В, С, … называются вероятностями этих событий).

Определение. Совокупность попарно несовместных событий образуют полную группу событий для данного испытания, если в результате каждого испытания происходит одно и только одно из них.

Примеры полных групп событий: а) выпадение герба и выпадение цифры при одном бросании монеты; б) попадание в цель и промах при одном выстреле по мишени; в) выпадение цифр «1», «2», «3», «4», «5», «6» при одном бросании кости.

Определение. События ω₁, ω₂, … , ω_n, образующие полную группу попарно несовместных и равновозможных событий, называются элементарными событиями.

Элементарными событиями являются выпадение цифр «1», … ,«6» при бросании кости. Эти события несовместны, равновозможны и образуют полную группу (предполагается, что кость является однородной и центрированной).

Множество всех элементарных событий называется пространством элементарных событий и обозначается Ω. Например, в результате бросания кости выпадение цифры i = 1, 2, 3, 4, 5, 6 образует пространство Ω = .

Элементарные события, составляющие пространство Ω, обозначаются ω₁, ω₂, …, ω₆.

Замечание. Кроме случайных событий в теории вероятностей вводятся в рассмотрение случайные величины. Случайная величина – это переменная, которая в результате испытания в зависимости от случая принимает одно из возможных значений. Случайные величины в данном пособии рассматриваются более подробно в главе 3.

Тест с ответами по теории вероятности

1.Указать верное определение.Суммой двух событий называется:

а ) Новое событие, состоящее в том, что происходят оба события одновменно;

б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;+

в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.

1. Указать верное определение.Произведением двух событий называется:

а ) Новое событие, состоящее в том, что происходят оба события одновременно;+

б ) Новое событие, состоящее в том, что происходит или первое, или второе, или оба вместе;

в ) Новое событие, состоящее в том, что происходит одно но не происходит другое.

1. Указать верное определение.Вероятностью события называется:

а ) Произведение числа исходов, благоприятствующих появлению события на общее число исходов;

б ) Сумма числа исходов, благоприятствующих появлению события и общего числа исходов;

в ) Отношение числа исходов, благоприятствующих появлению события к общему числу исходов;+

1. Указать верное утверждение. Вероятность невозможного события:

а ) больше нуля и меньше единицы;

в ) равна единице;

1. Указать верное утверждение. Вероятность достоверного события:

а ) больше нуля и меньше единицы;

в ) равна единице;+

1. Указать верное свойство. Вероятность случайного события:

а ) больше нуля и меньше единицы;+

в ) равна единице;

1. Указать правильное утверждение:

а ) Вероятность суммы событий равна сумме вероятностей этих событий;

б ) Вероятность суммы независимых событий равна сумме вероятностей этих событий;

в ) Вероятность суммы несовместных событий равна сумме вероятностей этих событий;+

1. Указать правильное утверждение:

а ) Вероятность произведения событий равна произведению вероятностей этих событий;

б ) Вероятность произведения независимых событий равна произведению вероятностей этих событий;+

в ) Вероятность произведения несовместных событий равна произведению вероятностей этих событий;

1. Указать верное определение.Событие это:

а ) Элементарный исход;

б ) Пространство элементарных исходов;

в ) Подмножество множества элементарных исходов.+

1. Указать правильный ответ. Какие события называются гипотезами?.

а ) любые попарно несовместные события;

б ) попарно несовместные события, объединение которых образует достоверное событие;+

в ) пространство элементарных событий.

1. Указать правильный ответ Формулы Байеса определяют:

а ) априорную вероятность гипотезы,

б ) апостериорную вероятность гипотезы,

в ) вероятность гипотезы.+

1. Указать верное свойство. Функция распределения случайной величины Х является:

а) невозрастающей; б) неубывающей; +в) произвольного вида.

1. Указать верное свойство. Равенство справедливо для случайных величин:

а) независимых+; б) зависимых; в) всех.

1. Указать верное свойство. Равенство справедливо для случайных величин:

а) независимых;+ б) зависимых; в) всех.

1. Указать правильное заключение.Из того, что корреляционный момент для двух случайных величин Х и Y равен нулю следует:

а) отсутствует функциональная зависимость между Х и Y;

б) величины Х и Y независимы;+

в) отсутствует линейная корреляция между Х и Y;

1. Указать правильный ответ. Дискретную случайную величину задают:

а) указывая её вероятности;

б) указывая её закон распределения;+

в) поставив каждому элементарному исходу в соответствие

1. Указать верное определение. Математическое ожидание случайной величины — это:

а) начальный момент первого порядка;+

б) центральный момент первого порядка;

в) произвольный момент первого порядка.

1. Указать верное определение. Дисперсия случайной величины- это:

а) начальный момент второго порядка;

б) центральный момент второго порядка;+

в) произвольный момент второго порядка.

1. Указать верную формулу. Формула для вычисления среднего квадратического отклонения случайной величины:

1. Указать верное определение. Мода распределения –это:

а) значение случайной величины при котором вероятность равняется 0,5;

б) значение случайной величины при котором либо вероятность, либо функция плотности достигают максимального значения ;+

в) значение случайной величины при котором вероятность равняется 0.

1. Указать верную формулу. Дисперсия случайной величины вычисляется по формуле:

1. Указатьвернуюформулу. Плотность нормального распределения случайной величины определяется по формуле:

1. Указать правильный ответ Математическое ожидание случайной величины распределенной по нормальному закону распределения , равно:

1. Указать правильный ответ. Математическое ожидание случайной величины распределенной по показательному закону распределения , равно:

1. Указать правильный ответ.Дисперсия случайной величины распределенной по показательному закону распределения , равна:

1. Указатьвернуюформулу. Для равномерного распределения математическое ожидание определяется по формуле :

1. Указать верную формулу. Для равномерного распределения дисперсия определяется по формуле :

1. Указать неверное утверждение. Свойства выборочной дисперсии:

а) если все варианты увеличить в одно и тоже число раз, то и дисперсия увеличится в такое же число раз.

б) дисперсия постоянной равняется нулю.

в) если все варианты увеличить на одно и тоже число, то выборочная дисперсия не изменится.+

1. Указать верное утверждение. Оценкой параметров называют:

а) Представление наблюдений в качестве независимых случайных величин имеющих один и тот же закон распределения.

б) совокупность результатов наблюдений;

в) всякую функцию результатов наблюдения.+

1. Указать верное утверждение. Оценки параметров распределений обладают свойством:

1. Указать неверное утверждение.

а) Метод максимального правдоподобия используется для получения оценок;

б) Выборочная дисперсия является смещенной оценкой для дисперсии;

в) В качестве статистических оценок параметров используются несмещённые, несостоятельные, эффективные оценки.+

1. Указать неверное утверждение. Для функции распределения двумерной случайной величины справедливы свойства:

1. Указатьневерноеутверждение:

а) По многомерной функции распределения всегда можно найти одномерные (маргинальные) распределения отдельных компонент.

б) По одномерным (маргинальным) распределениям отдельных компонент всегда можно найти многомерную функцию распределения.

в) По многомерной функции плотности всегда можно найти одномерные (маргинальные) плотности распределения отдельных компонент.

1. Указать правильное утверждение. Дисперсия разности двух случайных величин определяется по формуле:

1. Указать неверное утверждение. Формула вычисления совместной плотности :

1. Указать неверное утверждение. Случайные величины X и Y называются независимыми, если:

а) Закон распределения случайной величины X не зависит от того, какое значение приняла случайная величина Y.

в) коэффициент корреляции между случайными величинами X и Y равен нулю.

1. Указать правильный ответ. Формула является:

а) аналогом формулы Байеса для непрерывных случайных величин;

б) аналогом формулы полной вероятности для непрерывных случайных величин;+

в) аналогом формулы произведения вероятностей независимых событий для непрерывных случайных величин.

1. Указать неверное определение:

а) Начальным моментом порядка двумерной случайной величины (X,Y) называется математическое ожидание произведения на , т.е.

б) Центральным моментом порядка двумерной случайной величины (X,Y) называется математическое ожидание произведения центрированных на , т.е.)

в) Корреляционным моментом двумерной случайной величины (X,Y) называется математическое ожидание произведения на , т.е. +

1. Указать правильный ответ. Дисперсия случайной величины распределенной по нормальному закону распределения , равна:

1. Указатьневерноеутверждение. Простейшими задачами математической статистики являются:

а) выборка и группировка статистических данных, полученных в результате эксперимента;

б) определение параметров распределения, вид которого заранее известен;+

в) получение оценки вероятности изучаемого события.

Понятие события и его вероятности

Предмет теории вероятности

математический вероятность бейес производная

Математическая наука, изучающая общие закономерности случайных массовых явлений независимо от их конкретной природы и дающая методы количественной оценки влияния различных случайных факторов на рассматриваемые явления называется теорией вероятностей.

На основе наблюдений и опыта наука приходит к формулировке закономерностей, которым подчиняется течение изучаемых ею явлений. Простейшая и наиболее распространенная схема устанавливаемых закономерностей такова:

Предложение 1. При каждом осуществлении определенного комплекса условий происходит событие А.

Так, например, если вода при атмосферном давлении в 760 мм нагревается выше 100° по Цельсию (комплекс условий), то она превращается в пар (событие А). Или другой пример: при любых химических реакциях каких угодно веществ, без обмена с окружающей средой (комплекс условий) общее количество вещества (материи) остается неизменным (событие А). Последнее утверждение носит название закона сохранения материи. Читатель легко может самостоятельно указать примеры других подобных закономерностей, заимствованных из физики, химии, биологии и других наук.

Определение 1.Событие, которое неизбежно происходит при каждой реализации комплекса условий, называется достоверным.

Определение 2.Если событие A заведомо не может произойти при осуществлении комплекса условий, то оно называется невозможным.

Определение 3. Событие А, которое при реализации комплекса условий может произойти, а может и не произойти, называется случайным.

Из этих определений ясно, что, говоря о достоверности, невозможности, случайности какого-либо события, мы всегда будем иметь в виду его достоверность, невозможность или случайность по отношению к какому-либо определенному комплексу условий.

Простое утверждение о случайности события имеет очень ограниченный познавательный интерес: оно сводится лишь к указанию на то, что комплекс условий не отражает всей совокупности причин, необходимых и достаточных для появления события А. Такое указание нельзя считать совершенно бессодержательным, так как оно может послужить стимулом к дальнейшему изучению условий появления события А, но само по себе оно еще не дает нам положительного знания.

Имеется, однако, широкий круг явлений, когда при многократном осуществлении комплекса условий доля той части случаев, когда событие А происходит, лишь изредка уклоняется сколько-нибудь значительно от некоторой средней цифры, которая, таким образом, может служить характерным показателем массовой операции, (многократного повторения комплекса) по отношению к событию A.

Для указанных явлений возможно не только простое констатирование случайности события А, но и количественная оценка возможности его появления. Эта оценка выражается предложением вида:

Предложение 2. Вероятность того, что при осуществлении комплекса условий произойдет событие А, равна р.

Закономерности этого второго рода называются вероятностными или стохастическими закономерностями. Вероятностные закономерности играют большую роль в самых различных областях науки.

Несомненно, что понятие математической вероятности заслуживает углубленного философского изучения. И основная специфическая философская проблема, выдвигаемая самим существованием теории вероятностей и успешным ее применением к реальным явлениям, состоит в следующем: при каких условиях имеет объективный смысл количественная оценка вероятности случайного события А при помощи определенного числа Р(A), называемого математической вероятностью события А, и каков объективный смысл этой оценки. Ясное понимание взаимоотношения между философскими категориями случайного и необходимого является неизбежным предварительным условием успешного анализа понятия математической вероятности, но этот анализ не может быть полным без ответа на поставленный нами вопрос о том, при каких условиях случайность допускает количественную оценку в виде числа вероятности.

Число различных определений математической вероятности, предложенное теми или иными авторами, очень велико. Мы не станем сейчас разбираться во всех логических тонкостях этих многочисленных определений. Всякое научное определение такого рода основных понятий, как понятие вероятности, является лишь утонченной логической обработкой некоторого запаса очень простых наблюдений и оправдавших себя долгим успешным применением практических приемов. Интерес к логически безупречному «обоснованию» теории вероятностей возник исторически позднее, чем умение определять вероятности различных событий, производить вычисления с этими вероятностями, а также использовать результаты произведенных вычислений в практической деятельности и в научных исследованиях. Поэтому в основе большинства попыток научного определения общего понятия вероятности легко рассмотреть те или иные стороны конкретного познавательного процесса, приводящего в каждом отдельном случае к фактическому определению вероятности того или иного события, будь то вероятность выпадения хотя бы одной шестерки при четырех бросаниях игральной кости, или вероятность радиоактивного распада, или вероятность попадания в цель.

С очерченной сейчас точки зрения большинство определений математической вероятности может быть разделено на три группы:

• 1. Определения математической вероятности как количественной меры «степени уверенности» познающего субъекта — субъективная вероятность.
• 2. Определения, сводящие понятие вероятности к понятию «равновозможности» как к более примитивному понятию (так называемое «классическое» определение вероятности).
• 3. Определения, отправляющиеся от «частоты» появления события в большом количестве испытаний («статистическое» определение).

Указанные группы по отдельности обладают существенными недостатками и полное понимание природы вероятности требует их разумного синтеза.