Шень а игры и стратегии с точки зрения математики 2008

1. Введение.

Математические науки выделили собственную дисциплину, которая исключительно исследует игровые явления как явления, поддающиеся обработке математическим аппаратом. Истоки теоретико-игровых рассуждений восходят с работам Баше де Мезирака (середина 17 века). Сама же идея создания математической теории конфликта — теории игр — формируется с начала 20 века, о чем свидетельствуют труды К. Бутона, Э. Ласкера, Е. Мура, Э. Цермело, Э. Бореля, Г. Штейнгауза.

Теория игр представляет собой раздел математики, занимающейся исследованием вопросов поведения и разработкой оптимальных правил (стратегий) поведения каждого из участников в конфликтной ситуации.

Однако даже математическая теория игр не способна стопроцентно предопределить исход некоторых конфликтов.

Математические игры очень популярны, как, впрочем, и все игры. И далеко не всегда более сложная игра – более интересная. Часто миллионы людей с неугасаемым интересом играют в самые простые игры, и именно эти игры больше всего ценят, именно они входят в историю математики и прославляют своих создателей.

Простейшие математические игры часто используют как задачи, в которых нужно найти выигрышную стратегию, либо одно положение перевести в другое.

Иногда задачи бывают весьма простыми, когда они решаются известными методами, такими как инвариант и раскраска, но есть и весьма простые, но до сих пор неразрешённые задачи, связанные с математическими играми.

Что такое игровая, стратегическая задача? Это не совсем обычная математическая задача, так как, во-первых, в ней часто нет ничего числового, то есть непо­нятно, а что, собственно говоря, нужно решать или точнее, что писать в решении таких задач?

Во-вторых, иногда в играх нельзя придумать ал­горитм победы или, как говорят, стратегию победы, то есть иметь возмож­ность действовать определенным алгоритмическим образом в ответ на каждый ход противника, иными словами, в игре возможна победа и без стратегии, а также ничья.

В-третьих, для решения игровой задачи нужно уметь правильно записать его. И эта запись зависит, например, от того, кто выигрывает в данной игре.

Итак, сложностей при решении данного типа задач достаточно. Поэтому мы определяем следующую цель своей работы:

изучить новые методы решения нестандартных задач, классификацию данных методов; расширить свои знания по математике;

2. Основные идеи решения игровых задач

Как уже было сказано выше, для решения игровой задачи нужно уметь правильно записать его. И эта запись зависит, например, от того, кто выигрывает в данной игре.

Поэтому сначала рассмотрим общие правила записи решения игровых задач.

Так как же правильно записать решение игровой задачи?

В решении игровой задачи нужно записать:

I) ход первого игрока;

II) алгоритм ходов в ответ на каждый ход соперника, т. е. стра­тегию победы;

III) показать, что найдется независимо от хода соперника возможность сделать ход, т. е. его последний ход будет победным.

В работе рассмотрены следующие идеи стратегий:

Игры-шутки.

Игры, использующие симметрию.

Игры, в которых стратегия — дополнение до фиксированного числа.

Игры, использующие метод выигрышных позиций

Остановимся на каждой идее более подробно.

3. Игровые задачи.

1. Игры-шутки.

Игры – шутки – это такие игры, где для построения вы­игрышного алгоритма можно ничего и не знать, так как в них результат будет зависеть не от игры партнеров, а от начальных условий. Однако для этого в решении нужно заметить, что это игра-шутка, а не какая-то другая, в которой нужно искать выигрышную стратегию. На самом деле, нет никакой стратегии (а нас хотят обмануть, что она якобы есть!) Просто. как бы кто ни ходил, либо всегда выиграет первый игрок (тот, кто начинает игру), либо всегда второй. Задача — в том, чтобы математически доказать такую закономерность. Для доказательства обычно находится какая-то величина, которая понятно чему равна в начале и конце и понятно как изменяется на каждом ходу — тут даже частенько число ходов до конца однозначно посчитать можно. Это величина называется инвариантом (четность – самый известный инвариант в математике).

Инвариант (от лат. invarians — неизменяющийся), в математике — величина, остающаяся неизменяемой при тех или иных преобразованиях.

1. В ряде задач встречается следующая ситуация. Некоторая система последовательно изменяет своё состояние, и требуется выяснить нечто о её конечном состоянии. Полностью проследить за всеми переходами может оказаться делом сложным, но иногда ответить на требуемый вопрос помогает вычисление некоторой величины, характеризующей состояние системы и сохраняющейся при всех переходах (такую величину называют инвариантом для рассматриваемой системы). Ясно, что тогда в конечном состоянии значение инварианта будет то же самое, что и в начальном, т.е. система не может оказаться в состоянии с другим значением инварианта.

2. На практике этот метод сводится к тому, что некоторая величина вычисляется двумя способами: сначала она просто вычисляется в начальном и конечном состояниях, а затем прослеживается её изменение при последовательных мелких переходах.

3. Наиболее простым и часто встречающимся инвариантом является четность числа; инвариантом может быть также и остаток от деления не только на 2, но и на какое-нибудь другое число. Для построения инвариантов иногда бывают полезны вспомогательные раскраски, т.е. разбиения рассматриваемых объектов на несколько групп (каждая группа состоит из объектов одного цвета).

Многие задачи легко решаются, если заметить, что некоторая величина имеет определённую чётность. Из этого следует, что ситуации, в которых эта величина имеет другую чётность, невозможны. Иногда эту величину (функцию) надо сконструировать, например, рассмотреть чётность суммы или произведения, разбить объекты на пары, заметить чередование состояний, раскрасить объекты в 2 цвета.

Отметим, что часто для нахождения идеи решения задачи можно использовать «метод маленьких чисел», т. е. начинать поиск решения с небольших чисел.

Задача 1. Двое по очереди ломают шоколадку 5×8. За ход можно разломать любой кусок по прямой линии между дольками. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Решение: Долек всегда будет 5×8=40 штук, а шоколадка в начале была одна. Заметим, что на каждом ходу один кусок шоколадки всегда разламывается на 2, т.е. количество различных кусков шоколадки увеличивается на 1. В начале это кол-во было равно 1, а в конце, как мы заметили, 40. Значит, игра продолжалась ровно 39 ходов. Поэтому последний (39-й) ход был обязательно ходом первого (его ходы — первый, третий и все с нечетными номерами) — и первый выиграл.Вот такая получилась шутка — как ни ходи, первый всегда выигрывает.

Решить ту же задачу в общем виде, про шоколадку MxN.

Если число кусочков шоколадки четно, тогда побеждает первый, если число нечетно, тогда второй.

Задача – игра Ним.

Задача 2. Имеется три кучки камней: в первой — 10, во второй — 15, в третьей — 20. За ход можно разбить любую кучку на две меньшие. Проигрывает тот, кто не может сделать ход. Кто выиграет?

Решение: И это задача-шутка. Количество возможных ходов для раскладывания кучек: 45 – 3 = 42. Поэтому, как бы ни ходил первый игрок, при его ходе всегда будет четное число кучек. При хо­де же второго игрока количество кучек будет всегда нечетно. Значит, победит первый игрок, так как по окончании игры всегда остается ровно 45 кучек по одному камню в каждой.

2.Симметрия.Очень простой, но мощный и красивый метод решения игровых задач — симметричная стратегия. Суть его — делать каждый раз ход, симметричный ходу противника или дополняющий его до чего-либо. Доказательство правильности нашей стратегии будет пользоваться тем, что после каждого нашего хода позиция симметрична: раз так, то если противник сумел сделать свой ход, то и мы сможемсделать ход, симметричный ему.

Задача 1. Двое по очереди кладут пятаки на круглый стол так, чтобы они не накладывались друг на друга и не выступали за край стола. Про­игрывает тот, кто не может сделать ход. Кто выиграет?

Решение: Нам нужно найти такую последовательность ходов, которая позволила бы, глядя на ходы сопер­ника, делать ходы, которые привели бы к победе. Как же ходить после хода соперника? Стол круглый, поэтому первый ход так и просится — положить пятак в центр доски. А дальше? А дальше — по симметрии, относительно центра стола! И понятно, что первый выиграет.

Можно отметить, что если доска обладает центром симметрии (и не обязательно круглая), тогда первый сможет выиграть на ней, действуя аналогичным образом: ставя свою фишку или монету в центр стола, а затем используя центральную симметрию.

Заметим, что симметрия бывает не только центральной, но и осевой. Рассмотрим одну из таких задач.

Задача 2. Двое по очереди ставят слонов в клетки шахматной доски 8×8 так, чтобы слоны не били друг друга. Проигрывает тот, кто не может сделать ход. Кто выиграет?

Решение: Здесь нет центральной клетки. А если бы и была, по­ставить симметрично относительно нее слона мы не можем, так как тогда слон вставал на поле, которое бьется слоном, который поставил соперник.

Но шахматная доска обладает другим свойством симмет­рии. У нее целых четыре оси симметрии. Используем симметрию относительно оси, которая проходит параллельно одной из сторон доски. Тогда, ставя своего слона симметрично относительно этой оси слону, поставленному первым игроком, выигрывает второй игрок.

3. Игры, в которых стратегия — дополнение до фиксированного числа.

Другая идея выигрышной стратегии в играх — дополнение хода соперника до некоторого фиксированного числа, уменьшая каждым «совместным» ходом (т. е. ход первого и второго игрока) общее число элементов на некоторое постоянное число, что сводит игру к игре с меньшим числом элементов, т. е. более простой. Понятно, что победа в данной стратегии зависит от общего количества данных по условию элементов.

Рассмотрим пример такой стратегии на конкретной задаче.

Задача 1. Двое играют в игру. Ходы, которые делаются по очереди, заклю­чаются в том, что из кучки в 50 камней убирается любое число камней от 1 до 5. Выигрывает тот, кто возьмет последний камень. Кто выиграет в данной игре?

Решение: И опять выработку стратегии лучше начинать с небольшого числа камеш­ков. Понятно, что если в нашей кучке меньше шести камней, тогда выиграет первый игрок: он первым своим ходом заберет все камни.

Если бы в нашей кучке было 6 камешков, тогда понятно, что второй выиграет, так как он забрал бы все оставшиеся камни после первого хода начинающего.

Если камней семь? Что делать тогда первому? Ему нужно забрать один камень и свести задачу к предыдущему случаю. Аналогично надо выработать стратегию игры и для 7, 8, 9,10,11 камней.

Когда камней 12, то понятно, что выиграет второй: как бы первый не ходил, он своим ходом может взять такое количество камней, чтобы осталось ровно 6. А в этом случае он выигрывает, как мы уже разобрали.

Итак, если число камней делится на 6, то выигрывает второй, если не делится, то первый. Докажем это.

Пусть у нас 6tкамней. После первого хода игрока, начинающего игру, второй делает ход, после которого остается 6t — 6 камней, т. е. число камней в кучке уменьшилось на 6. Несложно понять, что послед­ний камень возьмет игрок, делающий второй ход, и также понятно, что у него всегда есть возможность сделать ход.

Пусть у нас 6t+a, где 1

Старт в науке

Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».

Математические игры и выигрышные стратегии. Игры с симметричной стратегией. Выигрышные позиции. Игры на шахматной доске.

Конспект занятия «Математические игры и стратегии.»

Игры и стратегии.

Игры и стратегии – отдельный класс математических задач. Чаще всего играют двое. При этом в условии оговорены правила игры. Нужно показать, какой из игроков имеет возможность выиграть независимо от ходов соперника.

В решении игровой задачи нужно записать:

I) ход первого игрока;

II) алгоритм ходов в ответ на каждый ход соперника, т. е. стратегию победы;

III) показать, что найдется независимо от хода соперника возможность сделать ход, т. е. его последний ход будет победным.

Основные (но не единственные) идеи стратегий:

Игры, использующие симметрию.

Игры, в которых стратегия — дополнение до фиксированного числа.

Игры, использующие метод выигрышных позиций

Сегодня на занятии мы подробно разберем каждую идею.

Игры – шутки – это такие игры, где для построения выигрышного алгоритма можно ничего и не знать, так как в них результат будет зависеть не от игры партнеров, а от начальных условий. Однако для этого в решении нужно заметить, что это игра-шутка, а не какая-то другая, в которой нужно искать выигрышную стратегию. На самом деле, нет никакой стратегии (а нас хотят обмануть, что она якобы есть!) Просто. как бы кто ни ходил, либо всегда выиграет первый игрок (тот, кто начинает игру), либо всегда второй. Задача — в том, чтобы математически доказать такую закономерность. Для доказательства обычно находится какая-то величина, которая понятно чему равна в начале и конце и понятно как изменяется на каждом ходу — тут даже частенько число ходов до конца однозначно посчитать можно. Это величина называется инвариантом (четность – самый известный инвариант в математике).

Инвариант (от лат. invarians — неизменяющийся), в математике — величина, остающаяся неизменяемой при тех или иных преобразованиях.

1. В ряде задач встречается следующая ситуация. Некоторая система последовательно изменяет своё состояние, и требуется выяснить нечто о её конечном состоянии. Полностью проследить за всеми переходами может оказаться делом сложным, но иногда ответить на требуемый вопрос помогает вычисление некоторой величины, характеризующей состояние системы и сохраняющейся при всех переходах (такую величину называют инвариантом для рассматриваемой системы). Ясно, что тогда в конечном состоянии значение инварианта будет то же самое, что и в начальном, т.е. система не может оказаться в состоянии с другим значением инварианта.

2. На практике этот метод сводится к тому, что некоторая величина вычисляется двумя способами: сначала она просто вычисляется в начальном и конечном состояниях, а затем прослеживается её изменение при последовательных мелких переходах.

3. Наиболее простым и часто встречающимся инвариантом является четность числа; инвариантом может быть также и остаток от деления не только на 2, но и на какое-нибудь другое число. Для построения инвариантов иногда бывают полезны вспомогательные раскраски, т.е. разбиения рассматриваемых объектов на несколько групп (каждая группа состоит из объектов одного цвета).

Многие задачи легко решаются, если заметить, что некоторая величина имеет определённую чётность. Из этого следует, что ситуации, в которых эта величина имеет другую чётность, невозможны. Иногда эту величину (функцию) надо сконструировать, например, рассмотреть чётность суммы или произведения, разбить объекты на пары, заметить чередование состояний, раскрасить объекты в 2 цвета.

Отметим, что часто для нахождения идеи решения задачи можно использовать «метод маленьких чисел», т. е. начинать поиск решения с небольших чисел.

Двое по очереди ломают шоколадку 5×8. За ход можно разломать любой кусок по прямой линии между дольками. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Решить ту же задачу в общем виде, про шоколадку MxN.

Имеется три кучки камней: в первой — 10, во второй — 15, в третьей — 20. За ход можно разбить любую кучку на две меньшие. Проигрывает тот, кто не может сделать ход. Кто выиграет?

На доске написаны цифры: 10 нулей и 10 единиц. За ход можно стереть две любые цифры и написать вместо них 0, если они были одинаковые или 1, если они были разные. Если на доске остается 1 — выигрывает первый. Если 0 — второй.

На доске записаны 2007 единицы и 2008 нулей. Каждый из двух игроков выбирает два произвольных числа, стирает, и записывает на их место 0, если они были равны, и 1, если нет. В конце на доске остается только одно число. Если это число 1, то выигрывает первый игрок, если 0, то второй. Кто выиграет?

Очень простой, но мощный и красивый метод решения игровых задач — симметричная стратегия. Суть его — делать каждый раз ход, симметричный ходу противника или дополняющий его до чего-либо. Доказательство правильности нашей стратегии будет пользоваться тем, что после каждого нашего хода позиция симметрична: раз так, то если противник сумел сделать свой ход, то и мы сможем сделать ход, симметричный ему.

Двое по очереди кладут пятаки на круглый стол так, чтобы они не накладывались друг на друга и не выступали за край стола. Проигрывает тот, кто не может сделать ход. Кто выиграет?

Двое играют, поочередно выставляя крестики и нолики на квадратном поле 9х9. В конце каждый получает очко за каждую строку и столбец, в которых его знаков больше. Сможет ли первый игрок выиграть?

Имеется две кучки камней — по 7 в каждой. За ход можно взять любое количество камней, но только из одной кучки. Проигрывает тот, кто не может сделать ход. Кто выиграет?

3. Игры, в которых стратегия — дополнение до фиксированного числа.

Другая идея выигрышной стратегии в играх — дополнение хода соперника до некоторого фиксированного числа, уменьшая каждым «совместным» ходом (т. е. ход первого и второго игрока) общее число элементов на некоторое постоянное число, что сводит игру к игре с меньшим числом элементов, т. е. более простой. Понятно, что победа в данной стратегии зависит от общего количества данных по условию элементов.

Рассмотрим пример такой стратегии на конкретных задачах.

Двое играют в игру. Ходы, которые делаются по очереди, заключаются в том, что из кучки в 26 камней убирается любое число камней от 1 до 5. Выигрывает тот, кто возьмет последний камень. Кто выиграет в данной игре?

Двое играют в игру, которая заключается в прибавлении к нулю любого натурального числа, не превышающего семи. Выигрывает тот, кто скажет число 50. Кто выиграет в данной игре?

5. Метод выигрышных позиций

Этот метод основан на рассмотрении каждой позиции с точки зрения пользы для игрока, которому предстоит ход. Начинаем рассматривать с конца – с последнего хода, затем предпоследний и т.д.

«Хромая ладья» может ходить по прямой вправо или вверх. Исходно она стоит в нижнем левом углу шахматной доски. Играют двое. Выигрывает тот, кто поставит ладью в верхний правый угол.

Имеются две кучки конфет: в одной — 20, в другой — 21. За ход нужно съесть все конфеты в одной из кучек, а вторую разделить на две необязательно равные кучки. Проигрывает тот, кто не может сделать ход. Кто выиграет?

Игры и стратегии. Задачи.

На концах клетчатой полоски 1 х 20 стоит по шашке. За ход разрешается сдвинуть любую шашку в направлении другой на одну или две клетки. Перепрыгивать через шашку нельзя. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

На столе лежит 25 спичек. Двое по очереди берут от 1 до 4 спичек. Проигрывает тот, кому спичек не осталось. Кто выигрывает при правильной игре? А если спичек 24?

На столе лежит 25 спичек. Двое по очереди берут 1, 2 или 4 спички. Проигрывает тот, кому спичек не осталось. Кто выигрывает при правильной игре?

На столе лежат 2 кучи спичек в одной 7, в другой 10. За один ход разрешается взять 1 спичку из одной (любой) кучки или по спичке из двух кучек сразу. Кто не может сделать ход (спичек не осталось) – проигрывает. Кто выиграет при правильной игре?

Попробуйте рассмотреть ту задачу на шахматной доске.

Имеется куча камней. Двое играющих берут по очереди 1, 2 ил 3 камня. Проигрывает тот, кто взял последний камень. Камни можно предварительно пересчитать. Как выиграть А, если он начинает игру?

Есть 2 кучи камней m и n . Каждый играющий берёт сколько угодно камней, но из одной кучи. Выигрывает тот, кто берёт последний камень. При каких m и n выигрывает первый, при каких второй и какая стратегия будет выигрышной?

В куче 25 камней. Два игрока берут по очереди или 2, или 4, или 7 камней. Проигрывает тот, у кого нет хода. Кто победит при правильной игре?

На доске записаны два числа: 2014 и 2015. Петя и Вася ходят по очереди, начинает Петя. За один ход можно

— либо уменьшить одно из чисел на его ненулевую цифру или на ненулевую цифру другого

— либо разделить одно из чисел пополам, если оно чётное.

Выигрывает тот, кто первым напишет однозначное число. Кто из них может выиграть, как бы ни играл соперник?

Задания по теме для самостоятельного решения

Играют двое. Начинающий называет одно из чисел: 1, 2, 3, 4. Второй игрок прибавляет к этому числу одно из этих же чисел: 1, 2, 3, 4 и называет вслух получившуюся сумму. То же самое делает затем первый игрок и т.д. Победителем считается тот, кто первым назовёт число 40. У которого игрока есть выигрышная стратегия? (в ответ запишите 1 или 2 – номер игрока).

Двое игроков делят 2 кучки конфет, 9 и 11, на более мелкие кучки. За 1 ход можно разделить 1 кучку на 2 меньших. Проигрывает тот, кто не сможет сделать ход. Сколько ходов в игре?

В ящике лежат 35 шариков. Двое играющих по очереди вынимают их из ящика, причём по условию игры каждый обязан вынуть в свой ход не менее одного и не более пяти. Проигравшим считается тот, кто вынужден будет при очередном своём ходе вынуть из ящика последний шар. Может ли игрок, делающий ход первым, обеспечить себе выигрыш? Сколько шариков он должен взять первым ходом? В ответ запишите число шариков на первом ходу.

Стратегические игры и решение задач. Вступление

Решил написать серию постов основанных чуть более, чем наполовину на тексте 2010 года составленным Хорди Деулофеу (Jordi Deulofeu). Опубликован DeAGOSTINI (Может быть ещё кем-то и где-то опубликован) в книге «Мир математики. Том 8. Дилемма заключенного и доминантные стратегии»

Глава о том, как, используя математику, выработать выигрышную стратегию в паре-тройке игр.

. Занимательная математика — это не только. разумное средство

заполнения досуга взрослых людей. Занимательная математика — это

прежде всего математика, причем в лучших своих образцах математика

прекрасная. Недаром видный английский математик Дж. Литлвуд заметил,

что хорошая математическая шутка лучше дюжины посредственных работ.

Игры можно классифицировать различными способами в зависимости от выбранного критерия: место для игры, число участников, длительность партии, уровень сложности и так далее.

Применительно к математике игры можно разделить на две большие группы в зависимости от того, присутствуют в них случайные события или нет. Случайные события могут фигурировать как в начальных условиях игры, так и при совершении ходов.

• Например, в большинстве карточных игр карты раздаются игрокам случайным образом. Так же происходит и в домино.

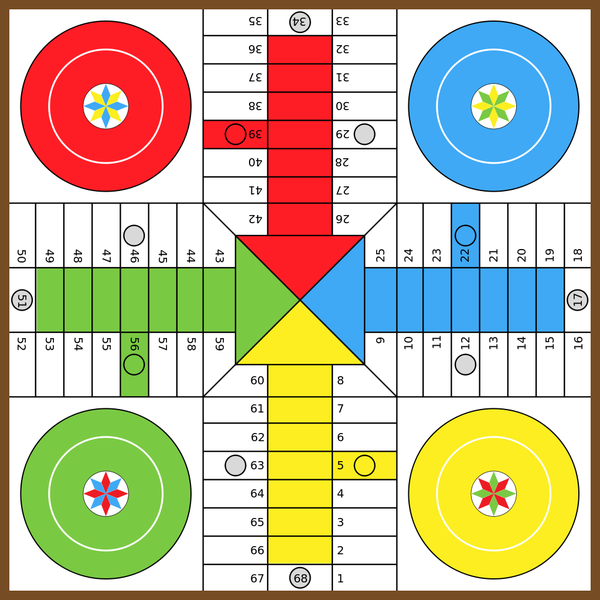
• Напротив, начальное положение шахматных фигур строго определено и неизменно, как и в нардах, реверси или испанской игре парчис.

Если говорить о случайности ходов, то во многих играх игроки свободно выбирают следующий ход из всех возможных, в то время как в других играх ходы зависят от броска одной или нескольких игральных костей. В этом случае игрок выбирает лишь из нескольких ходов, возможных для выпавшего числа очков на игральных костях.

Доска для игры парчис на 4-х игроков.

Стратегическими называются игры, в которых никогда не происходит случайных событий. Всё определяют только решения игроков. Благодаря отсутствию случайности, игры этого типа можно проанализировать и найти способ победить.

В некоторых случаях можно полностью определить выигрышную стратегию, в других ввиду сложности игры это не удастся, но можно показать, что подобная стратегия существует для одного из игроков. Несмотря на очевидное разнообразие игр такого типа, к ним применимо ограниченное число математических понятий и приемов, которые относятся преимущественно к арифметике (системы счисления и признаки делимости) и геометрии (равновесные ситуации, главным образом, симметрия).

Понятие выигрышной стратегии

В математике слово «игра» может обозначать как собственно игру, в которой участвует более одного игрока, имеются определенные правила, а цель игры — одержать победу в партии, так и математические развлечения и головоломки. В дальнейшем мы будем говорить об играх, в которых участвуют минимум два игрока. Эти игры также можно разбить на группы разными способами, но с точки зрения математики существует признак, определяющий две большие группы: игры с полной информацией и игры, в которых присутствует элемент неопределенности. В этой главе игры первой группы будем называть стратегическими, игры второй группы — азартными.

Как следует изучив игру, возникает вопрос: какие ходы нужно совершать, чтобы одержать победу в определенной партии? В азартных играх этот вопрос не имеет смысла, поскольку игроки лишь двигают фишки согласно выпавшим очкам на игральных костях и следуют инструкциям на игровых клетках. Иными словами, здесь нет места для принятия решений, поэтому нет «хороших» или «плохих» игроков. Результат игр подобного типа полностью зависит от случая, поэтому определить какую-либо выигрышную стратегию невозможно. В этом смысле можно сказать, что интересность игры с точки зрения математики равна нулю.

Другой крайний случай — игры с полной информацией, в которых в любой момент можно узнать все возможные ходы и их последствия (как минимум в теории) и нет места неопределенности. Из всех подобных игр нам больше всего знакомы шахматы, хотя подобных стратегических игр, как традиционных (го, манкала, шашки, крестики-нолики), так и современных (гекс, ним, реверси, абалон и другие), существует великое множество.

Японские гейши играют в го, автор — Эйдзан, 1811 год

Когда мы говорили об анализе игр этого типа, мы упомянули понятие выигрышной стратегии, то есть множества условий, позволяющих одному из игроков (как правило, речь идет об играх только для двух игроков) определить, как следует действовать в каждый момент времени, учитывая ходы, сделанные противником, чтобы одержать победу вне зависимости от ходов соперника. Существование выигрышной стратегии предполагает, что игра оканчивается победой одного из игроков, но в некоторых играх возможна и ничья, например, как в шахматах. В этом случае нужно вести речь о стратегиях, которые позволяют никогда не проигрывать. Когда стратегическая игра не может завершиться ничьей, можно убедиться, что существует выигрышная стратегия для первого или второго игрока, но это не означает, что подобную стратегию можно будет точно определить: игра может быть весьма сложной.

Допустим, что некая игра для двух игроков имеет следующие свойства:

1. В любой момент времени каждый игрок обладает всей информацией, чтобы решить, каким должен быть следующий ход.

2. Игроки совершают ходы поочередно.

3. В игре полностью отсутствует элемент неопределенности.

4. Любая партия оканчивается победой одного из игроков после конечного числа ходов.

При этих условиях можно показать, что обязательно существует выигрышная стратегия для одного из двух игроков: первого (игрок А) или второго (игрок Б). Допустим, что выигрышной стратегии для игрока А не существует, иными словами, для игрока Б всегда будет существовать ход, на который у игрока А не найдется достойного ответа, и он проиграет. Это означает, что победит игрок Б. Таким образом, для него существует выигрышная стратегия. Подобные рассуждения лишь доказывают, что в подобных играх всегда существует выигрышная стратегия, но это не означает, что ее будет легко обнаружить.

Для игр, в которых партия не обязательно содержит конечное число ходов, применимость этого утверждения зависит от принятия так называемой аксиомы выбора. Эта известная и противоречивая математическая аксиома утверждает, что для каждого семейства (конечного или бесконечного) непустых непересекающихся множеств существует новое множество, образованное путем выбора определенного элемента из каждого множества этого семейства. С помощью этой аксиомы Банах, Мазур и Улам в 1930 году определили бесконечную игру и доказали, что в ней не существует выигрышной стратегии ни для одного из игроков.

Ну вот пока всё. Следующий пост будет о том, как использовать преимущества и как определять стратегии. Найдём формулу победы в игре Ним и ей подобным.

Игры и стратегии с точки зрения математики, Шень А., 2008

Игры и стратегии с точки зрения математики, Шень А., 2008.

Хотите верьте, хотите нет — но либо в шахматах у белых есть гарантированный выигрыш, либо у чёрных есть гарантированная ничья.

В этой брошюре рассказывается, что это значит, почему это верно (хотя и бесполезно
в шахматной практике!), какие ещё бывают подобные игры и как их можно математически анализировать.

Первое издание книги вышло в 2007 г.

1. Введение
2. Несколько простых примеров
3. Классификация позиций
4. Игра «ним»
5. Симметрия
6. Выигрышные стратегии: разное
7. Изоморфизм игр
8. Игры с многими исходами
9. Формальные определения и доказательства
10. Теоремы существования
11. Игры Шпрага — Гранди
12. Программирование игр
13. Бесконечные игры
14. Игры с неполной информацией

Пример.
Двое играют в такую игру. Один зажимает в кулаке рублёвую или двухрублёвую монету, второй пытается угадать, какая монета зажата. Если второй угадал, монета переходит к нему, если нет, то он платит штраф в полтора рубля. Вопрос: как вы думаете, честная ли это игра или один из игроков имеет преимущество? Оказывается, что нечестная. Чтобы сделать её честной, нужно изменить размер штрафа. Попробуйте поставить этот вопрос математически и найти ответ на этот вопрос. Это не так просто — математическая теория игр такого рода была разработана в середине XX века фон Нейманом и Моргенштерном.

Сейчас этот раздел математики относят к «математической экономике». (Не то чтобы это было уж так полезно для практической экономики, скорее наоборот — такое название облегчает получение финансирования этих исследований.) Недавно был популярен американский фильм «Игры разума»; прототипом главного героя этого фильма является американский математик Джон Нэш, получивший нобелевскую премию по экономике как раз за работу в этой области — доказательство существования так называемого равновесия Нэша в играх двух лиц с неполной информацией. К сожалению, авторы фильма вместо вразумительного изложения определений и формулировки теоремы Нэша (отсутствие доказательства им можно простить — у них же фильм, а не сериал) предпочли изображать «духовный мир математика» и сделали это довольно убого.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Игры и стратегии с точки зрения математики, Шень А., 2008 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Игры и стратегии

Игры и стратегии с точки зрения математики

Издание второе, стереотипное

Москва Издательство МЦНМО 2008

Ш47 Игры и стратегии с точки зрения математики. | изд., стереотипное. | М.: МЦНМО, 2008. | 40 с.: ил.

Хотите верьте, хотите нет | но либо в шахматах у белых есть гарантированный выигрыш, либо у чёрных есть гарантированная ничья. В этой брошюре рассказывается, что это значит, почему это верно (хотя и бесполезно в шахматной практике!), какие ещё бывают подобные игры и как их можно математически анализировать.

Первое издание книги вышло в 2007 г.

Электронная версия книги является свободно распространяемой и доступна по адресу ftp://ftp.mccme.ru/users/shen/games.zip

В оформлении обложки использована акварель на пергаменте (ок. 1320) со страницы http://commons.wikimedia.org/wiki/Image:Meister der Manessischen Liederhandschrift 004.jpg

Акварель входит в Manessische Liederhandschrift (Szene: Schachspiel), хранится в библиотеке Гейдельберга, входит в The Yorck Project: 10.000 Meisterwerke der Malerei, 2003, ISBN 3936122202, distributed by DIRECTMEDIA Publishing GmbH и предоставлена для Wikimedia Common (директор издательства и The Yorck Project, Erwin Jurschitza, говоря о предоставленных файлах, пишет, что Jedes einzelne Bild ist Public Domain , см.

Рецензент и редактор Николай Александрович Яковлев

Игры и стратегии с точки зрения математики

Подписано в печать 15.10.2008 г. Формат 60 × 90 1 / 16 . Бумага офсетная. Печать офсетная. Печ. л. 2,5. Тираж 3000 экз. Заказ Ђ 1973

Издательство Московского центра непрерывного математического образования 119002, Москва, Большой Власьевский пер., 11. Тел.

Отпечатано с готовых диапозитивов в ППП «Типография » Наука\». 121009, Москва, Шубинский пер., 6.

c Шень А., 2007, 2008

Спросите у знакомого шахматиста, кто выигрывает в шахматах | белые или чёрные. «Что за глупый вопрос, | ответит он вам | смотря кто играет за белых и за чёрных и как сложится игра.» Ну а если оба играют наилучшим образом, что тогда? Оказывается, что поставленный таким образом вопрос имеет вполне точный смысл. Правда, ответ на него неизвестен. Но можно доказать, что имеет место ровно одна из трёх возможностей:

• у белых есть способ, позволяющий им гарантированно выиграть, как

бы ни играли чёрные;

• у чёрных есть способ, позволяющий им гарантированно выиграть, как

бы ни играли белые;

• у белых есть способ, позволяющий им гарантированно не проиграть

(=выиграть или свести игру вничью), и одновременно у чёрных есть способ, позволяющий им гарантированно не проиграть.

Чтобы доказать это, даже не надо быть шахматистом. Как мы увидим, подобные утверждения верны для большого класса игр, называемого «конечные игры с полной информацией». Мы разберём также много примеров таких игр; в некоторых случаях нам удастся выяснить, какой из случаев имеет место, и даже указать наилучший способ игры (или, как говорят, стратегию ).

Советуем не спешить читать объяснения, приводимые после описания игры. Сначала попробуйте разобраться с этой игрой сами!

2. Несколько простых примеров

1 На столе лежит 25 спичек. Играющие по очереди могут взять от одной до четырёх спичек. Кто не может сделать ход (спичек не осталось), проигрывает.

Другими словами, выигрывает взявший последнюю спичку.

В этой игре второй игрок может гарантировать себе выигрыш. Для этого он должен дополнять ход первого до пяти спичек (если первый взял одну, второй берёт четыре и т. п.). Тогда после хода второго сначала останется 20 спичек, затем 15, затем 10, 5 и, наконец, 0 | первый проиграл.

2 А что будет, если изначально не 25 спичек, а 24?

В этом случае выигрывает первый: он должен взять четыре спички, останется 20, а затем дополнять ход противника до 5 спичек.

Легко понять, что будет в общем случае, для N спичек. Если N делится на 5 без остатка, то второй может гарантировать себе выигрыш, дополняя ход противника до 5. Если же N не делится на 5 без остатка, то выигрывает

первый. Он должен сначала взять столько спичек, каков остаток, а потом дополнять ход противника до 5.

3 На столе лежат две кучки спичек: в одной 10, в другой | 7. Игроки ходят по очереди. За один ход можно взять любое число спичек (1 ; 2 ; 3 ; : : : ) из одной из кучек (по выбору игрока). Кто не может сделать ход (спичек не осталось), проигрывает.

Здесь первый игрок может гарантировать выигрыш, если сначала уравняет кучки, взяв три спички из большей. После этого он должен повторять ходы второго, но брать из другой кучки, восстанавливая нарушенное равенство.

4 Что будет в этой игре, если изначально в одной кучке m спичек, а в

Если m 6 = n , то выигрывает первый: он должен своим ходом уравнять

кучки, а потом поддерживать равенство. Если же m = n , то игроки меняются местами: второй может восстанавливать равенство после нарушения его первым, тем самым обеспечив себе выигрыш.

5 Шоколадка представляет собой прямоугольник 5 × 8, разделённый

углублениями на 40 квадратиков. Двое по очереди разламывают её на части по углублениям: за один ход можно разломить любой из кусков (больший одного квадратика) на два. Кто не может сделать хода (все куски уже разломаны), проигрывает.

В этой игре | удивительным образом | не имеет значения, как ходить. Что бы ни делали игроки, шоколадку можно разломить ровно 39 раз, не больше и не меньше. (Не верите? Посчитайте ходы при разных вариантах разломов.)

Дело в том, что при каждом разломе число кусков увеличивается ровно на 1. В начале игры был 1 кусок (вся шоколадка), а в конце 40 кусков (квадратиков). Значит, всего было 39 ходов. Первый игрок при этом делал нечётные ходы (с номерами 1 ; 3 ; 5 ; : : : ; 39). Поэтому он сделал последний ход, то есть выиграл.

Выигрышу первого игрока не может помешать не только второй игрок, но даже и сам первый (в отличие, скажем, от шахмат, где неудачный ход может быть роковым).

6 Двое игроков пишут двадцатизначное число слева направо, по очереди приписывая к нему по одной цифре. Первый игрок выигрывает, если полученное число не делится на 7, второй | если делится.

Последнюю (крайнюю правую) цифру пишет второй игрок. До этого момента он может выбирать любые цифры. В последний момент он должен

выбрать среди десяти возможностей ту, при которой полученное число разделится на 7. (Среди десяти последовательных натуральных чисел всегда есть хотя бы одно, делящееся на 7, а иногда даже два.)

7 Что будет, если в предыдущей игре заменить 7 на 13?

В этом случае прежнее рассуждение не годится: среди десяти последовательных чисел может не быть ни одного делящегося на 13. И действительно, ситуация меняется и первый может гарантировать выигрыш, правильно выбрав предпоследнюю цифру. Выбирая предпоследнюю цифру, первый выбирает десяток внутри сотни подряд идущих чисел; второй затем выбирает одно число из этого десятка. Первый выиграет, если в выбранном им десятке не будет ни одного числа, делящегося на 13. Такой десяток всегда найдётся. Ведь если бы во всех десяти подряд идущих десятках нашлось по числу, делящемуся на 13, то всего таких чисел было бы как минимум десять среди ста идущих подряд, чего быть не может.

Следующие три игры попробуйте проанализировать сами (и выяснить, кто выигрывает при правильной игре).

8 Первый называет целое число, затем второй называет ещё одно. Если сумма чисел чётна, выигрывает первый, если нечётна | второй.

9 (Продолжение) Тот же вопрос, если вместо суммы берут произведение чисел.

10 Дан выпуклый Игроки по очереди проводят в нём диагонали, не пересекая проведённых ранее (во внутренних точках). Тот, кто не может сделать ход, проигрывает. (Это случится, когда многоугольник будет разрезан на треугольники.)

3. Классификация позиций

Мы разобрали несколько примеров игр. В каждом из них мы указали, кто из игроков может гарантировать себе выигрыш и как для этого он должен играть. Но как до этого догадаться? Иногда это удаётся сделать, проанализировав игру «с конца». Для примера рассмотрим самую первую игру, но немного изменим условие.

11 На столе лежит 25 спичек. Играющие по очереди могут взять 1, 2 или 4 спички. Кто не может сделать ход (спичек не осталось), проигрывает.

Разница в том, что брать три спички нельзя, так что правило «дополнять ход противника до пяти спичек» теперь не годится (если противник взял две). Чтобы проанализировать игру, изобразим возможные варианты

(сколько осталось спичек) кружочками, а возможные ходы | стрелками. (На рисунке 1 поместились лишь небольшие количества спичек, но картинку можно продолжить влево.) Из каждого кружочка идут три стрелки, соот-

9 87654321

Рис. 1. Граф позиций для игры со спичками.

ветствующие трём возможным ходам (прямая стрелка | взять одну спичку, кривые | взять две или четыре спички). Скажем, если у нас 9 спичек (левый кружочек), то после нашего хода может остаться 8, 7 или 5 спичек, и это изображено стрелками.

Такие картинки математики называют ориентированными графами ; кружочки называются вершинами графа, а стрелки | рёбрами (или дугами ) графа.

Будем анализировать ситуацию справа налево, глядя на картинку.

• Если к нашему ходу спичек не осталось, то мы проиграли.

• Если к нашему ходу осталась одна спичка, то мы можем выиграть, взяв

её | противник останется без спичек и проиграет.

• То же самое, если осталось две или четыре спички | мы выигрываем

• А что будет, если нам осталось три спички? Взять все три по правилам

мы не можем. Можно взять одну или две. В этом случае противнику останется две или одна, и он выиграет (взяв их на своём ходу). Поэтому три спички | проигрышная позиция (для того, чей сейчас ход).

• Про четыре спички мы уже говорили. Если осталось пять спичек, то мы

можем взять две и оставить противнику три, передав ему ход в проигрышной позиции. Значит, пять спичек | выигрышная позиция.

• Если осталось шесть спичек, то можно взять одну, две или четыре.

Тогда у противника будет 5, 4 или 2 спички. Все эти позиции для него выигрышные, так что шесть спичек | проигрышная позиция.

• Раз шесть спичек | проигрышная позиция, то 7, 8 и 10 | выигрыш-

ные. В самом деле, взяв 1, 2 или 4 спички, мы оставим противнику 6.

• Девять спичек | проигрышная позиция: при любом ходе противник

оказывается в выигрышной позиции с 8, 7 или 5 спичками. Всё это показано на рисунке 2.

Легко сообразить, что дальше всё будет повторяться с периодом 3: позиции, где число спичек делится на 3, будут проигрышными (для того, кто в них оказался), а где не делится | выигрышными. В частности, в игре с 25 спичками, с которой мы начинали, выигрывает первый игрок.

9 87654321

Рис. 2. Выигрышные и проигрышные позиции.

Как он должен при этом играть? Он должен ставить противника в проигрышную позицию, то есть брать столько спичек, чтобы осталось кратное трём количество. (Заметим, что при этом он может никогда не брать четыре спички, достаточно брать одну или две.)

Тем же способом можно проанализировать и другие игры. Разберём ещё один пример.

12 В одной из клеток шахматной доски стоит «односторонняя ладья», которая может двигаться влево или вниз. Двое игроков ходят по очереди, сдвигая ладью влево или вниз на любое число клеток (но не менее одной); кто не может сделать ход, проигрывает.

Здесь удобно записывать буквы В и П (для выигрышных и проигрышных позиций) прямо на доске. Позиция в левом нижнем углу проигрышная (наша очередь хода, а ходить некуда). Остальные позиции на первой горизонтали и первой вертикали выигрышные, так как из них можно подвинуть ладью в угол и поставить противника в проигрышную позицию (рис. 3).

П В В В В В В В

Рис. 3. Односторонняя ладья: начало анализа.

Далее замечаем, что позиция b2 (вторая вертикаль, вторая горизонталь) проигрышная, поскольку любой ход из неё (вниз или влево) даёт противнику выигрышную позицию. А другие позиции на этой горизонтали и этой вертикали выигрышные, так как из них можно перевести ладью на b2 (рис. 4).

Игры и выигрышные стратегии

Определение игры

Человек с самого детства и всю жизнь играет в игры. И если некоторое представление о детских, логических и компьютерных играх имеют все, то далеко не все знают, что, например, выбор банка, в котором следует открыть счет, — это тоже игра (в математическом смысле слова). В математике существует специальный раздел — теория игр, в котором изучаются свойства игр в широком смысле.

Определимся сразу, что мы будем рассматривать не все игры, а только их определенный класс. Нас будут интересовать игры с противоречивыми интересами сторон (антагонистические игры) и полной информацией об игре, и в первую очередь такая разновидность подобных игр, как игра двух лиц с нулевой суммой.

Игра двух лиц (в дальнейшем будем называть их первый игрок и второй игрок, подразумевая игроков, которые ходят первым и вторым соответственно) с нулевой суммой означает, что выигрыш одного игрока является проигрышем другого (в ряде игр возможна ничья).

В рассматриваемых нами играх участвуют два игрока, которые ходят по очереди, причем оба они обладают полной информацией о текущей игровой ситуации (это определение исключает большинство карточных игр) и о возможных ходах очередного игрока. Игра считается оконченной, если достигнута позиция, являющаяся согласно правилам игры “терминальной” (конечной, заключительной), например, матовая позиция в шахматах. Правилами игры также устанавливается, каков исход игры в этой терминальной позиции.

Чтобы задать конечную игру с полной информацией 4 , нужно:

· указать конечное множество, элементы которого называются позициями игры;

· указать начальную позицию игры;

· указать множество заключительных позиций и задать результат игры в каждой из них;

· для каждой из остальных позиций указать возможные ходы, т.е. позиции, которые могут случиться после хода первого или второго игрока соответственно (в некоторых играх возможные ходы не зависят от того, какой именно игрок ходит).

При этом в игре не должно быть бесконечных партий (бесконечных последовательностей позиций, в которых игроки ходят по правилам, но так и не попадают в заключительную позицию).

Если к тому же ни в каких аспектах игры (правилах, возможности или очередности ходов, определении момента завершения игры или результата) не участвует элемент случайности, такая игра будет еще и детерминированной.

Примерами рассматриваемых нами игр являются большинство настольных игр: шахматы, шашки, го, крестики-нолики, реверси и многие другие. В математике большое распространение получили игры с камнями, в которых в распоряжении двух игроков имеются несколько кучек камней (одна или более). Игроки ходят по очереди. Также определено, сколько камней и из какого количества кучек может взять игрок за один ход. Если за один ход можно взять любое ненулевое число камней, но только из одной из кучек, то такая игра называется ним. Позициями в таких играх являются различные состояния кучек, которые можно получить из начального состояния (очевидно, что в каждой из кучек может оказаться не больше камней, чем было изначально). Пусть у нас было n кучек по k камней в каждой. Тогда общее число позиций равно (k + 1) n . Здесь учитывается, что в каждой из кучек в процессе игры камней может и не остаться. Поэтому в первой кучке может находиться от 0 до k камней, для каждого состояния первой кучки во второй также может находиться от 0 до k камней и т.д. Часть позиций, возможно, неотличимы друг от друга с точки зрения игры. Заключительной является единственная позиция, в которой ни в одной из кучек камней не осталось. Обычно по правилам она считается проигрышной (тот, кто не может сделать очередной ход, проигрывает), но можно считать ее и выигрышной, тогда такую игру называют “в поддавки”.

Классификация позиций и стратегии игроков

Пусть в нашей игре не бывает “ничьих” и игроки ходят по очереди. Нетерминальная позиция называется выигрышной, если в ней существует какой-нибудь разрешенный ход, приводящий к выигрышу. С другой стороны, некоторая нетерминальная позиция является проигранной для игрока, если все разрешенные ходы из этой позиции ведут к позициям, в которых возможен выигрыш противника. Запишем это более формально.

Нетерминальная позиция x называется выигрышной для игрока, которому предоставлен ход, если существует хотя бы один ход, переводящий игру в проигрышную позицию. Нетерминальная позиция x называется проигрышной, если все ходы из позиции x ведут в выигрышные позиции.

Стратегией в конечной игре с полной информацией называется правило, указывающее, как следует игроку ходить в каждой из позиций, где ход за ним. Понятие стратегии не надо отождествлять с понятием хода. Стратегия определяет полный план действий игрока при всевозможных ситуациях, могущих возникнуть в игре.

Стратегия называется выигрышной для игрока, если все партии, в которых он придерживается этой стратегии, заканчиваются выигрышем этого игрока. Покажем, что в рассматриваемом нами классе игр обязательно существует выигрышная стратегия для одного из игроков, а все позиции игры можно разделить на выигрышные и проигрышные.

Конечную игру с полной информацией можно представить в виде ориентированного графа (см. “Структуры данных”), вершинами которого являются все допустимые позиции игры, а ребра указывают возможные ходы. Данный граф обязательно будет ациклическим (не будет содержать циклов), в противном случае окончание игры не гарантировано. Будем назначать значение для каждой вершины этого графа (выигрышная или проигрышная) по таким правилам:

· значение вершин, соответствующих терминальным позициям, однозначно определено правилами игры;

· все вершины, из которых хотя бы одно ребро графа ведет в вершину, помеченную как проигрышную, помечаем как выигрышные;

· все вершины, из которых все ребра графа ведут в выигрышные позиции, помечаем как проигрышные.

Эти правила применяем в любом порядке, пока это возможно. Утверждается, что рано или поздно всем позициям игры будут присвоены определенные значения. В самом деле, если какая-то вершина графа оказалась непомеченной, то она не может быть заключительной. Более того, какая-то из следующих за ней позиций тоже осталась непомеченной (иначе мы смогли бы пометить и эту), значит, и у нее какая-то из следующих не имеет пометки и т.д.
В результате мы получаем бесконечную партию, которая по условию невозможна.

Так как все позиции оказались помеченными, то помечена и начальная позиция. Если она оказалась выигрышной, то при правильной игре первый игрок гарантированно выигрывает и его выигрышная стратегия состоит в том, чтобы на каждом ходу ставить противника в проигрышную позицию (наличие такого хода обеспечено правилом, по которому помечалась соответствующая вершина графа). Если же она помечена как проигрышная, то гарантированно выигрывает второй игрок при любом ходе первого игрока.

Из доказанного утверждения следует, что результат многих логических игр, в том числе и шахмат, предсказуем. Почему же мы не только не знаем выигрышную стратегию для большинства популярных игр, но открытым остается и вопрос, кто имеет гарантированный выигрыш в каждой из них? Дело здесь в астрономическом числе возможных позиций. Например, в шахматах это число оценивают сверху как 10 120 . Оно находится за пределами возможностей компьютеров в обозримом будущем.

Программирование игр

Говоря даже об определенном классе игр, нельзя не упомянуть компьютерные программы, играющие в различные игры из данного класса. Как, например, компьютеры играют (и, как мы знаем, весьма успешно) в шахматы? Ведь полный анализ данной игры пока невозможен. Как и люди, компьютеры просчитывают варианты для текущей позиции — они смотрят, какие возможны ходы, какие ответы возможны на каждый из ходов и т.д. Просмотр приходится на каком-то уровне прерывать и грубо оценивать позицию как выигрышную или проигрышную в зависимости от материального перевеса и расположения фигур. К этому еще добавляется библиотека начал (дебютов), накопленная многовековым опытом шахматистов, а также сведения об окончаниях (эндшпилях), часть из которых, в свою очередь, удалось за последние годы просчитать на компьютере.

Если же игра такова, что число позиций в ней, по меркам современных компьютеров, не велико (скажем, не превосходит 10 6 ), то игру можно полностью просчитать, начиная с терминальных позиций. Соответствующая программа будет существенно более эффективной, если значения уже просчитанных позиций будут запоминаться в памяти компьютера и не пересчитываться повторно. Для этого, помимо прочего, надо научиться все позиции нумеровать (в ряде игр это может быть весьма нетривиальной задачей). При этом часть позиций можно будет и не просчитывать вообще: если для какого-то хода игрока выясняется, что он ведет в проигрышную позицию, то другие варианты хода можно уже не рассматривать (текущая позиция выигрышная).

К счастью, для ряда игр просчитывать большое число позиций для определения результата игры не требуется. В них удается выигрышную стратегию описать с помощью простой функции, аргументом которой является позиция, а значением — выигрышный ход для данной позиции или сообщение о том, что позиция является проигрышной. Рассмотрим пример такой игры 5 .

На столе лежат N камней. Играющие по очереди могут взять от одного до четырех камней. Кто не может сделать ход (камней не осталось) — проигрывает. Если N делится на 5 без остатка, то второй игрок может гарантировать себе выигрыш, дополняя ход противника до 5 (если первый взял одну, то второй берет четыре и т.д.). Если N на 5 не делится, то выигрывает первый игрок: он должен сначала взять число камней, равное остатку от деления N на 5, а потом дополнять ход противника до 5. Здесь все позиции с числом камней кратным 5 являются проигрышными, остальные — выигрышными. Программирование выигрышной стратегии для такой игры не составит труда.

Часто в играх используется и так называемая “симметричная стратегия”. Например, двое игроков кладут одинаковые круглые монеты на прямоугольный стол. Монеты могут свешиваться за край, но не должны падать и перекрываться. Кто не может положить монету — проигрывает. В этой игре первый игрок может выиграть, положив первым ходом свою монету в центр стола, а затем повторяя ходы второго игрока симметрично относительно центра. Очевидно, что если второй игрок нашел место для монеты, то есть и пустое симметричное ему место. В этой игре число позиций бесконечно (хотя сама игра конечна), но идея симметрии применяется и в ситуациях с конечным числом позиций.

Методические рекомендации

Тема выигрышные стратегии в играх появилась в профильном уровне стандарта среднего (полного) общего образования по информатике. Изучение темы “Игры и выигрышные стратегии” позволяет показать ученику научный подход к решению ряда бытовых задач, расширяет их кругозор с точки зрения практической применимости знаний математики и алгоритмов. Ранее подобные задачи встречались лишь на олимпиадах по информатике и программированию и опирались на знания, полученные учащимися математических классов в углубленном курсе математики. Начиная с 2005 г. задачи на поиск выигрышной стратегии встречаются и в материалах ЕГЭ по информатике. Приведем пример задачи из демоверсии ЕГЭ 2007 г.

Задача. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 3, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет один камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Решение. Выигрывает второй игрок.

Для доказательства рассмотрим неполное дерево игры, оформленное в виде таблицы, где в каждой ячейке записаны пары чисел, разделенные запятой. Эти числа соответствуют количеству камней на каждом этапе игры, в первой и второй кучах соответственно. Приведенная на с. 36 таблица содержит все возможные варианты ходов первого игрока. Из нее видно, что при любом ходе первого игрока у второго имеется ход, приводящий к победе.

В бескомпьютерном варианте предлагаемые задачи по информатике на данную тему таковы, что общее число позиций в игре позволяет провести практически полный ее анализ так, как было рассказано в материалах статьи.

Программирование стратегий одного из игроков в различных логических играх может стать хорошей темой для кружковой и внеклассной работы учащихся (подготовка к конференциям, турнирам игровых программ, в которых программы играют между собой, и т.п.).

4 См. книгу А.Шеня “Игры и стратегии с точки зрения математики”. М.: изд-во МЦНМО, 2007.

5 Игра приведена, в частности, в книге А.Шеня “Игры и стратегии с точки зрения математики”.