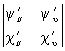Поверхность с точки зрения геометрии это

Мир поверхностей разнообразен и безграничен. Он простирается от элементарной, отличающейся простотой и математической строгостью плоскости, до сложнейших, причудливых форм криволинейных поверхностей, не поддающихся точному математическому описанию.

Без преувеличения можно сказать, что по разнообразию форм и свойств, по своему значению при формировании различных геометрических фигур, по той роли, которую они играют в науке, технике, архитектуре, изобразительном искусстве, поверхности не имеют себе равных среди других геометрических фигур.

Естественно, что начертательная геометрия как наука, передающая результаты своих теоретических исследований в распоряжение инженера для их практического использования, не может обойти вниманием такие важные геометрические фигуры, какими являются поверхности.

ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F (х, у, z) = 0, где F (х, у, г) — многочлен n-й степени, или в форме какой-либо трансцендентной функции. В первом случае поверхности называют алгебраическими, во втором — трансцендентными.

Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается n-го порядка. Любая произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет сама поверхность. Порядок поверхности может быть определен также числом точек ее пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).

В начертательной геометрии геометрические фигуры задаются графически, поэтому целесообразно рассматривать поверхность как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии. Образование поверхности с помощью линии позволяет дать иное определение поверхности, базирующееся на основных элементарных геометрических понятиях, таких, как точка и множество. Действительно, если принять, что положение движу-щейся в пространстве линии будет непрерывно меняться с течением времени t, и принять t за параметр, то поверхность можно рассматривать как непрерывное однопараметрическое множество линий. В свою очередь, линия определяется как непрерывное однопараметрическое множество точек, поэтому можно дать следующее определение поверхности: поверхностью называется непрерывное дву параметрическое множество точек.

Поверхность, имеющая два измерения

• одна из двух частей крыла летательного аппарата

• одно из основных понятий геометрии

• поверхность, имеющая два измерения

• ровная, гладкая поверхность

• Ровная, гладкая поверхность

• Одно из основных понятий геометрии, поверхность, имеющая два измерения

• Одна из двух частей крыла летательного аппарата

• Область, сфера рассмотрения чего-нибудь, точка зрения

• (устар.) плоские, тривиальные слова, тривиальность

Поверхность с точки зрения геометрии это

О понятии тела и его поверхности в геометрии

В предыдущем изложении мы неоднократно употребляли слова тело и поверхность тела, вкладывая в их содержание известные вам наглядные представления. Теперь мы дадим определение геометрического тела и его поверхности.

Точка фигуры называется внутренней, если существует шар с центром в этой точке, целиком принадлежащий фигуре. Фигура называется областью, если все ее точки внутренние и если любые две ее точки можно соединить ломаной, целиком принадлежащей фигуре. Поясним данное определение на примере шара (рис. 463).

Каждая точка шара, которая удалена от его центра на расстояние r, меньшее R, является внутренней точкой шара, так как шар с центром в этой точке и радиусом R — r содержится в исходном шаре радиуса R. Все точки шара, которые удалены от центра на расстояние, меньшее R, образуют область. В самом деле, любые две такие точки А и В соединяются отрезком АВ, все точки которого удалены от центра на расстояние, меньшее R.

Точка пространства называется граничной точкой данной фигуры, если любой шар с центром в этой точке содержит как точки, принадлежащие фигуре, так и точки, не принадлежащие ей. Для шара граничными точками являются точки, которые удалены от точки О на расстояние, равное R, т. е. граница шара есть сфера. Для каждой такой точки С можно указать в каждом шаре с центром С и радиусом r>0 точки С₁ и С₂, отстоящие от точки О на расстояние, большее R, и на расстояние, меньшее R.

Область вместе с ее границей называется замкнутой областью.

Телом называется конечная замкнутая область. Граница тела называется поверхностью тела. Шар является примером тела. Другими знакомыми нам примерами тел являются многогранник, цилиндр и конус.

Подобно тому как в пространстве, на плоскости вводятся понятия внутренней точки фигуры, граничной точки и области. Граничные точки области образуют границу области. В круге радиуса R точки, которые находятся на расстоянии, меньшем R, от центра, внутренние, а точки, находящиеся на расстоянии R, граничные. Круг — замкнутая область.

Плоский многоугольник — это ограниченная замкнутая область на плоскости, граница которой является многоугольником.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Поверхность

Одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.

1) В школьном курсе геометрии рассматриваются плоскости, многогранники, а также некоторые кривые поверхности. Каждая из кривых П. определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, П. шара — множество точек, отстоящих на заданном расстоянии от данной точки. Понятие «П.» лишь поясняется, а не определяется. Например, говорят, что П. есть граница тела или след движущейся линии.

2) Математически строгое определение П. основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). Более точно, простой П. называется образ гомеоморфного отображения (т. е. взаимно однозначного и взаимно непрерывного отображения) внутренности квадрата (см. Гомеоморфизм). Этому определению можно дать аналитическое выражение. Пусть на плоскости с прямоугольной системой координат u и υ задан квадрат, координаты внутренних точек которого удовлетворяют неравенствам 0

В дифференциальной геометрии исследуемые П. обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости П., т. е. существования в каждой точке П. определённой касательной плоскости, кривизны и т.д. Эти требования сводятся к тому, что функции φ(u, υ), Ψ(u, υ), χ(u, υ) предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. Кроме того, требуется, чтобы в каждой точке хотя бы один из определителей

, ,

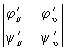
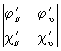
В аналитической геометрии и в алгебраической геометрии П. определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:

Таким образом, определённая П. может и не иметь наглядного геометрического образа. В этом случае для сохранения общности говорят о мнимых П. Например, уравнение

определяет мнимую сферу, хотя в действительном пространстве нет ни одной точки, координаты которой удовлетворяют такому уравнению (см. также Поверхности второго порядка). Если функция Ф (х, у, z) непрерывна в некоторой точке и имеет в ней непрерывные частные производные 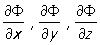, из которых хотя бы одна не обращается в нуль, то в окрестности этой точки П., заданная уравнением (*), будет правильной П.

Основы геометрии. Определения основных элементов, пятый элемент

С самого раннего детства, когда мы не то что говорить, даже ходить не умеем, наш мозг уже включается в работу постижения окружающего мира. Мы рассматриваем и ощупываем окружающие нас предметы и таким образом получаем первые познания о форме и размерах — главных понятиях геометрии, которая незримо будет сопровождать нас всю жизнь. Конечно, можно сказать, что

длина, ширина и высота — это числовые характеристики размеров объекта

вот только это абстрактное определение содержит больше вопросов, чем ответов и потому даже первоклассник такое определение вряд ли поймет. Между тем даже трехлетний ребенок, гуляя на улице, находит самую длинную палку, а если вы ее заберете и дадите взамен более короткую, то ребенок вполне может и расплакаться. Из чего следует, что понятие длины ребенку хорошо знакомо, даже если он еще никогда в жизни слова такого не слыхал.

Ну а для определения формы предмета нужно знать еще несколько понятий. Их Евклид сформулировал настолько просто, что даже сейчас понимание некоторых из них вызывает определенные сложности. Сколь полезной для гимнастики ума была новая трактовка евклидовых определений, я уже писал выше. А здесь я просто изложу свое понимание геометрии, далеко не всегда совпадающее с трактовкой Евклида и других геометров, однако с использованием аналогий к системе координат Декарта (также одного из комментаторов Евклида). Вообще-то прообразом системы координат является крест, использовавшийся людьми за тысячи лет до появления христианства, и смысл у него был приблизительно такой же как и у нынешней системы координат, но к кресту мы еще вернемся. В отличие от описательных определений Евклида я постараюсь дать большей частью генетические определения:

Первый и простейший элемент геометрии — точка, точнее геометрическая точка

Применять к точке понятия размеров или формы бессмысленно, если точка только одна. Точка изначальна, как слово в библии, но без точки невозможна геометрия, все остальные геометрические фигуры состоят как бы из точек. Впрочем, это утверждение справедливо только для моего абстрактного геометрического мира. Не все точки одинаково важны при решении задач геометрии, но обсуждать этот вопрос более подробно, пока мы ничего кроме точек не знаем, не имеет смысла.

Второй важнейший элемент геометрии — это линии

линии бывают разными. На мой взгляд наиболее важными из них являются:

2.1. Элементарный отрезок

Элементарный отрезок образован двумя точками, а значит появляется расстояние между точками, условно говоря — длина, а так как рассматривается элементарный отрезок, то это некое элементарное расстояние, в данном случае длина.

Примечание 1: В классической геометрии не используются понятия элементарного отрезка, элементарных размеров, элементарной поверхности и др. С одной стороны это значительно упрощает решение многих практических задач, а с другой стороны плохо соотносится с наблюдаемым нами реальным миром. Например, любое наблюдаемое нами твердое тело реального мира, имеющее некоторую массу, состоит из атомов, во всяком случае атомистическая модель строения мира пока не опровергнута. В однородном (изотропном) пространстве расстояние между атомами определяется взаимодействием атомов тела и если на тело не действуют никакие силы кроме указанной силы взаимодействия, то расстояние между атомами будет приблизительно одинаковым и для тела из данного материала элементарным. Т.е. определять какие-либо геометрические характеристики для некоего условно однородного материала с межатомным расстоянием 0.3 нм на расстоянии 0.15 нм от одного из атомов бессмысленно, тем не менее классическая геометрия это допускает. Впрочем геометрия используется не только для определения размеров материальных тел. Уникальность геометрии в том, что она как пустой горшок Винни Пуха, может вместить в себя что угодно. Например, если речь идет о траектории движения некоей материальной точки, то такая траектория также может рассматриваться как геометрическая фигура и тогда понятие элементарного отрезка становится весьма условным, так как в этом случае расстояния между точками траектории действительно можно рассматривать стремящимися к нулю. Это иногда приводит к другим парадоксам, не разрешимым с точки зрения классической геометрии, но о них речь ниже.

Элементарный отрезок — одномерен. Пользуясь аналогией с системой координат можно сказать, что отрезок измеряется только по одной оси, например оси х. Например, для ребенка, который нашел палку, важна только длина, на остальные характеристики он пока не обращает внимания и мы не будем.

Из отрезков может слагаться линия сколь угодно большой длины. Таким образом можно сказать, что любая линия — это множество точек, однако такое определение будет не совсем полным. Более точным будет следующее определение:

2.2. Линия — это множество расстояний между точками

однако с точки зрения геометрии нет необходимости рассматривать каждое расстояние между точками отдельно, если свойства линии не меняются. Достаточно знать расстояние между начальной и конечной точкой, что и является главной характеристикой для элементарного отрезка. Это значительно упрощает решение задач. Таким образом для определения свойства линии достаточно знать характеристики главных точек. Я бы назвал эти точки характерными точками.

2.3. Самая простая линия — это прямая линия

Прямая линия, как и просто линия — это множество расстояний между точками, свойства же прямой линии меняются только в двух точках, в начале и в конце. Можно сказать, что прямая линия характеризуется расстоянием между начальной и конечной точкой или что сумма расстояний между соседними точками равна расстоянию между крайними точками. Однако самым лучшим на мой взгляд будет следующее определение: Для полного описания прямой линии достаточно указать расстояние между начальной и конечной точками .

Прямая линия одномерна. Это означает, что прямую линию всегда можно расположить так, что наблюдатель будет видеть только одну начальную точку. Например, когда школьник, плюющий через трубочку жеванной бумагой в понравившуюся девочку, приставляет к глазу трубочку, чтобы посмотреть на мишень, он как раз и совмещает центр окружности начала трубочки с центром окружности конца трубочки, а по ходу и все центры поперечных сечений трубочки, если трубочка ровная.

Прямая линия подобна элементарному отрезку. Единственное отличие — в длине.

Прямая линия — частный случай всех возможных линий, тем не менее важность прямой линии для геометрии очень велика. В реальном мире к прямой линии приближаются, например, траектория падения камня под действием силы тяжести, или форма нити отвеса, который также притягивается к земле силой тяжести. Приближаются, а не соответствуют потому, что на камень, падающий в земной атмосфере, также действует сила сопротивления воздуха, порывы ветра, возможно другие факторы, влияющие на траекторию полета и тем самым нарушающие прямолинейность траектории. Для нити кроме указанных факторов также немаловажными будут свойства материала нити и особенности ее изготовления. Однако геометрия, оперируя понятием прямой линии в случаях, когда вышеуказанными факторами можно пренебречь, значительно упрощает решение задач.

Линия — это грань, граница между чем-либо, которую мы вполне отчетливо себе представляем, хотя в реальном мире никакой реальной границы может и не быть, а есть просто оптический эффект. Например, черный квадрат Малевича был бы невозможен на полностью черном фоне, т.е. без границ, условно говоря, линий, отделяющих черное от белого. Вот только сама по себе линия одномерного мира мало что значит, ей нужно что-то разделять или ограничивать.

Пока все вроде бы просто и достаточно понятно, но

Есть в геометрии такая линия, которая и очень простая и очень сложная одновременно — это окружность

Дать определение окружности не смог даже Евклид. Оно ведь как получается, с одной стороны окружность — это множество точек, расположенных на одинаковом расстоянии от центра окружности (современное определение), да только Евклид не рассматривал линии, как множество точек, а мыслил их как некий элемент геометрии, не имеющий прямого отношения к точкам. А с другой стороны, если рассматривать окружность, как линию, образованную элементарными отрезками, то получается, что окружность — можно составить из коротких прямолинейных отрезков. А значит окружность — это просто ломаная замкнутая линия. Например, из трех элементарных отрезков можно составить равносторонний треугольник, но треугольник — явно не окружность, из четырех — квадрат, но и это никак не окружность по виду, равносторонние пятиугольник и шестиугольник и т.д. выглядят уже лучше, но все равно от окружности далеки. И тут вспоминается древнейший софистический парадокс, звучавший примерно так: «Одно зерно — не куча, два — зерна — не куча, три зерна — не куча и если прибавлять по одному зерну, то куча никогда не получится». А между тем, что такое куча зерна мы очень хорошо себе представляем. Куча — это когда много зерна. Примерно то же самое можно сказать и о окружности:

Окружность — это когда прямолинейных отрезков, образующих окружность, настолько много, что они представляются одной сплошной линией

Между тем современная геометрия рассматривает окружность, как некую плавную замкнутую линию, которую сколько ни разбивай на отрезки, они все равно будут не прямолинейными. Это приводит к тому, что даже сейчас невозможно совершенно точно определить длину окружности, да и площадь круга даже теоретически. Т.е. многие из вас слышали про число П, но не многие знают, что это постоянное число, выражающее отношение длины окружности к радиусу, точно рассчитать не возможно, так как П является иррациональным и трансцендентальным числом. Использовать точное значение числа П для абсолютного большинства расчетов нет никакой практической необходимости, поэтому люди обычно пользуются приближенным значением П, допускающим некоторый, хотя и очень малый, но процент погрешности. Вот и выходит, что как окружность ни крути, а она все еще остается загадкой. Ну а чтобы закруглить этот парадокс, отмечу, что в современной геометрии прямая линия может рассматриваться, как часть окружности с бесконечно большим радиусом, т.е. является как бы элементарным отрезком. Такие дела.

Третий важный элемент геометрии — это поверхности

Поверхности, как и линии бывают разными, причем разнообразие поверхностей еще больше, чем линий.

3.1. Элементарная поверхность

Основная характеристика элементарной поверхности — площадь и вообще можно назвать элементарную поверхность элементарной частью площади. Для определения площади элементарной поверхности недостаточно знать только длину, необходимо оперировать еще и шириной. Таким образом элементарная поверхность — это уже элемент двухмерного мира. Как и линия, поверхность образована точками, минимум тремя, или линиями, как минимум тремя. Но с точки зрения классической геометрии это не совсем так. В геометрии Эвклида поверхность качественно новый элемент геометрии, связанный с предыдущими тем, что поверхность ограничивается линиями, поэтому определение поверхности как некоего элемента главная характеристика которого — площадь, вполне допустима.

3.2. Из элементарных поверхностей может слагаться поверхность сколь угодно большой площади

При этом как и в случае с линиями рассматривать все расстояния между точками вовсе не обязательно и даже расстояния между всеми линиями, которые могут быть образованы из этих точек — тоже не обязательно. Достаточно знать характеристики главных линий, я бы назвал эти линии характерными линиями. Характерные линии ограничивают поверхность, например черный квадрат Малевича ограничен 4 линиями.

3.3. Самая простая поверхность — плоская поверхность или как сейчас говорят — плоскость

Плоскость двухмерна, это означает, что плоскость всегда можно расположить так, что наблюдателю будет видна только одна линия. Например, плотники с древнейших времен проверяют точность обработки деревянного бруса, смотря на исследуемую поверхность так, чтобы линия, ограничивающая начало поверхности, совпала с линией, ограничивающей конец поверхности.

Плоскость — это частный случай всех возможных плоскостей, но как и прямая линия, плоскость очень важна для решения задач геометрии. Более того, прямая линия и плоскость интуитивно понятны даже людям, никогда геометрию не изучавшим. Например, когда человеку нужно добраться из точки А в точку В, то он старается проложить маршрут, максимально близкий к прямой линии, а если путь будет проходить по равнине, а не по пересеченной местности, то совсем хорошо. А еще люди делают тоннели в горах и засыпают овраги, чтобы сделать дорогу из одного пункта в другой максимально приближающейся к прямой линии.

И точка и линия и поверхность в геометрии могут рассматриваться и как отдельные элементы и как формообразующие элементы, например, точка формообразующий элемент для линии, а линия формообразующий элемент для поверхности. Также точка, линия и поверхность могут быть общими элементами геометрических фигур.

Для основной части школьного курса геометрии этих элементов вполне достаточно, да и у Евклида трехмерные геометрические фигуры рассматриваются в книгах XI-XIII. Тем не менее хочется закончить этот ряд.

Четвертый важный элемент геометрии — это тело

Тело — это трехмерная геометрическая фигура. Большинство предметов окружающего нас мира представляют собой трехмерные тела. Основная характеристика тела — объем. Для определения объема тела недостаточно знать только длину и ширину, нужно знать еще и высоту. Ограничивается тело поверхностями.

4.1. Элементарное тело — это тело, имеющее элементарный объем

Например, при определении свойств материалов с кристаллической решеткой используется понятие — элементарная ячейка кристаллической решетки, характеризуемое расстояниями между атомами решетки. Суть этого понятия в том, что для определения геометрических свойств решетки нет необходимости рассматривать все элементарные ячейки, достаточно описать свойства только элементарной ячейки. Очень условно элементарное тело можно рассматривать, как подобие элементарной ячейки кристаллической решетки.

4.2. Из элементарных тел может быть образовано тело сколь угодно большого объема

4.3. Самое простое тело — это куб, так как оно ограничено плоскостями, при этом плоскости ограничены прямыми линиями

А теперь закончим этот ряд:

Линия, состоящая из нескольких элементарных отрезков, может быть одномерной, двухмерной и трехмерной. Поверхность, состоящая из нескольких элементарных поверхностей, может быть двухмерной и трехмерной. Тело любое — только трехмерным. С точки зрения геометрии (если условия задачи позволяют) любое из окружающих нас материальных тел, имеющих вполне определенный объем, может рассматриваться, как геометрическая точка.

Например, если нужно определить расстояние от одной звезды до другой, то учитывать при этом объемы звезд и уточнять, что определяется расстояние между центрами звезд, вовсе не обязательно, так как расстояние между звездами значительно больше чем диаметры звезд. Другими словами, если подобное уточнение даст изменение результата в пределах нескольких тысячных процента и даже менее, то нет большого смысла тратить время на подробные вычисления.

Примечание 2: Считается, что первым теорию относительности сформулировал Эйнштейн, однако основы теории относительности сформулировали далекие предки Эйнштейна — шумеры, даже задолго до Евклида. Ведь они первые ввели понятие процента. А процент — это и есть основа теории относительности. Ведь что такое, например расстояние между двумя звездами в 100000 световых лет или состояние человека в 100000 денежных единиц? Это некие абсолютные величины, по большому счету человеку ни о чем не говорящие. А вот рассмотрение этих величин по отношению к чему-либо сильно влияет на человеческое восприятие. Например, если на эти самые 100000 денежных единиц можно купить 5 булочек, то это в общем-то хорошо, но на прожить не хватит. А вот если на эти же самые 100000 денежных единиц можно купить 5 хлебобулочных заводов — это совсем другое дело. Недаром процент с древнейших времен использовался как один из важнейших критериев оценки окружающего нас мира. Конечно, современное понятие процента намного шире, но подробное рассмотрение этого понятия в цели данной статьи не входит.

Таким образом в геометрии есть 4 формообразующих элемента из которых может быть образована любая геометрическая фигура. Эти перечисленные выше элементы характеризуются абсолютными характеристиками длиной, шириной и высотой

Рисунок 1. а) Условное изображение физического тела, состоящего из атомов

б) геометрическая модель физического тела или просто геометрическое тело

На рисунке 1.б) точка показана фиолетовым цветом, линия — малиновым цветом, плоскость — розовым цветом. А еще любое тело можно рассматривать, как образованное некоторым количеством параллельных плоскостей, а если эти плоскости имеют постоянную высоту и ширину, то как и в случае с прямой линией рассматривать все эти плоскости совершенно не обязательно, достаточно определить основные характеристики только для одной плоскости. Так современный школьный курс геометрии на 90% посвящен рассмотрению свойств плоских фигур. Теперь, после ознакомления с формообразующими элементами можно бы и начать более полное изучение геометрии, но

В геометрии есть еще один очень важный элемент, который по праву можно назвать пятым элементом — это угол

Угол — это часть целого и вместе с тем относительная характеристика геометрических фигур

По большому счету длина, ширина и высота также не являются абсолютными характеристиками, например длина линии — это расстояние между двумя точками, а значит характеристика одной точки относительно другой. Тем не менее размеры можно считать абсолютными понятиями по отношению к такой характеристике как угол. Особенность угла в том, что размеры линий, поверхностей или тел, образовавших данный угол, не имеют принципиального значения. Для определения угла важно только взаимное расположение геометрических фигур, угол образовавших.

Как и другие элементы геометрии, углы бывают разными, но как правило для решения большинства задач геометрии люди используют малую часть возможных углов. Так из всех возможных углов чаще всего рассматривается плоский угол. Такой угол может быть образован двумя линиями, находящимися в одной плоскости.

Из плоских углов наибольшее значение имеет прямолинейный угол. Такой угол образован не просто линиями, а прямыми линиями, что позволяет определить характеристики угла максимально просто.

Из прямолинейных углов выделяются еще два частных случая: прямой угол и развернутый угол.

Если при пересечении двух прямых образуются 4 одинаковых угла, то такие углы называются прямыми, а линии называются перпендикулярными друг другу

А в целом такие прямые образуют упоминавшийся нами крест — древнейший человеческий оберег, используемый людьми задолго до появления христианства и символизирующий защиту от темных сил со всех четырех сторон света. Мне кажется вполне вероятным, что если бы наши предки использовали понятие трех сторон света или трех времен года, то современная геометрия была бы совсем другой, так как в процессе человеческого познания нет ничего не нужного и не важного. Кстати и сейчас некоторое целое может быть разбито углами на 360 частей, называемых градусами, когда-то эти 360 частей означали количество дней в календарном году и были получены разбиением зодиакального круга. Изображение зодиакального круга можно увидеть во вступительной статье.

Если прямая образована из отрезков, то угол между всеми отрезками является развернутым

Это означает, что никаких изменений параметров в общих точках не происходит, что позволяет рассматривать не каждый отрезок прямой линии в отдельности, а всю прямую линию в целом. Таким образом развернутый угол — это как бы показатель стабильности. Например, если четыре нижних точки на рисунке 1.а) соединить отрезками, то в итоге мы получим прямую линию состоящую из трех отрезков.

Также тут стоит упомянуть и о нулевом угле. Например, если рассматривать две прямые, расположенные в одной плоскости (например, прямые ограничивающие плоскость на рисунке 1.б) сверху и снизу), то угол между ними условно можно считать нулевым или развернутым в зависимости от того, какие точки будут приниматься за начало линий. Условно — потому что не существует точки пересечения параллельных прямых (в евклидовой геометрии), а значит и угла никакого нет, ни нулевого ни развернутого.

Главными характеристиками угла в свою очередь являются синус и косинус

Значения синуса и косинуса можно условно сравнить с коэффициентом полезного действия. Коэффициент полезного действия — очень важный показатель для человека, чем ближе этот показатель к 100% или к единице, тем человеку приятнее, проще говоря, никто не любит делать дурную работу.

Так синус прямого угла равен единице или 100%, а синус развернутого угла и нулевого угла = 0. Попробуем проиллюстрировать это на примере определения площади плоской геометрической фигуры. Например плоскость, показанная на рисунке 1.б) может рассматриваться как план комнаты. Комната образована 4 линиями — стенами. При этом даже если длина стен будет постоянной и одинаковой, то площадь комнаты может сильно изменяться в зависимости от значения углов между стенами:

На рисунке 2 показаны плоские геометрические фигуры образованные прямыми линиями одинаковой длины. При этом даже без подробных расчетов понятно, что максимальная площадь будет у квадрата — рисунок 2.а). Квадрат — это частный случай прямоугольника. А прямоугольник — это такая плоская фигура, ограниченная параллельными линиями, у которой длина боковых линий равна высоте фигуры, а кроме того углы между всеми сторонами — прямые.

А вот если строители плохо учились в школе и не выдержали прямые углы между стенами, при этом длина стен не изменилась, то вполне может получиться ромб, показанный на рисунках 2.б) или 2.в). Это может показаться шуткой, но я в своей жизни такие комнаты наблюдал неоднократно, хотя и не в таком явном виде, как показано на рисунках. Ромб — плоская геометрическая фигура, у которой все стороны равны и соответственно противоположные границы параллельны, однако углы между смежными линиями не равны прямому. Как видно из этих рисунков, чем больше угол между смежными линиями отличается от прямого, тем меньше площадь фигуры.

Если повернуть левую боковую сторону на все 90 о , то в итоге получится линия, равная сумме длин нижней и боковой сторон и вообще никакой площади не имеющая, так как у линии никакой высоты нет.

Площадь показанных на рисунке 2 фигур равна произведению длины на высоту. Длина у всех фигур условно одинаковая — это нижняя стена, а вот высота (показана на рисунке 2 синим цветом) — разная. А высота во всех случаях равна произведению длины боковой стороны на синус угла между смежными стенами. Вот и получается, что синус как бы показывает коэффициент полезного действия, т.е. при прямом угле между смежными сторонами квадрата площадь квадрата максимальна, а при нулевом угле (развернутом угле) площадь равна нулю.

А если рассматривать геометрическую фигуру, образованную боковой стеной, высотой и красной линией, то это будет прямоугольный треугольник, вписанный в окружность. Если длина боковой стены — радиуса окружности = 1, то синяя линия — это синус угла, а еще противолежащий катет, а красная линия — это косинус угла, а еще прилежащий катет, а боковая наклонившаяся стена — гипотенуза. Таким образом косинус прямого угла равен нулю, а косинус развернутого угла = -1, косинус нулевого угла = 1.

Получить такие геометрические фигуры можно с помощью обычного детского магнитного конструктора. Достаточно взять 4 палочки и 4 шарика и соединить их между собой так, чтобы получился квадрат, а затем надавить соответствующим образом на один из шариков. При этом квадрат будет постепенно превращаться в ромб, показанный на рисунке 2.б), а если давить и дальше, то и в ромб, показанный на рисунке 2.в. При этом общая точка для нижней и левой боковой линии станет центром вращения для левой боковой стороны, а сама левая боковая сторона станет радиусом окружности.

Конечно же человеку, решая различные возникающие перед ним задачи, приходится иметь дело не только с прямым и развернутым углом, но также и со всеми остальными. А чтобы каждый раз не вычислять значения синуса, косинуса и других тригонометрических функций, люди пользуются соответствующими таблицами или калькулятором, который сам все посчитает, для того он и придуман.

Это далеко не все, что можно рассказать о формообразующих элементах, но для начала хватит.

Надеюсь, уважаемый читатель, информация, представленная в данной статье, помогла вам хоть немного разобраться в имеющейся у вас проблеме. Также надеюсь на то, что и вы поможете мне выбраться из той непростой ситуации, в которую я попал недавно. Даже и 10 рублей помощи будут для меня сейчас большим подспорьем. Не хочу грузить вас подробностями своих проблем, тем более, что их хватит на целый роман (во всяком случае мне так кажется и я даже начал его писать под рабочим названием «Тройник», на главной странице есть ссылка), но если я не ошибся в своих умозаключениях, то роману быть и вы вполне можете стать одним из его спонсоров, а возможно и героев.

После успешного завершения перевода откроется страница с благодарностью и адресом электронной почты. Если вы хотите задать вопрос, пожалуйста, воспользуйтесь этим адресом. Спасибо. Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 0121 5641

Кошелек webmoney: R158114101090

Категории:

• Расчет конструкций . Основы прикладной геометрии

Оценка пользователей: Нет Переходов на сайт: 9182 Комментарии:

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Геометрия поверхностей

1) Понятие поверхности. Определение поверхности.

Def. Под элементарной поверхностью (простой поверхностью) понимают любые семейства точек, которые можно топологично отобразить на замкнутый круг.

Замечание. Локально (в малом) поверхность получается в результате непрерывной деформации в (гомоморфизм) плоской области.

Глобально (в целом) поверхность «склеивается» из таких кусков.

Def. Поверхностью называют множество точек, состоящих из конечного или счетного множества простых поверхностей склеенных друг с другом.

Будем рассматривать поверхности, которые гомоморфны некоторой плоской области D. Область D – область плоскости переменных u и v.

Замечание. Гомоморфизм же области D в пространстве , в результате которого и возникает рассматриваемая поверхность, обычно задают, выбрав … — т. О и вектор-функцию .

2) Способы задания поверхности:

а) векторно-параметрический: r = r(u,v).

б) если в введена прямоугольная система координат:

r(u,v) = х(u,v)i + y(u,v)j + z(u,v)k

в) в частном случае, когда из уравнений и подставим в явное уравнение поверхности

г) неявное задание поверхности:

Замечание. Мы будем изучать регулярные или дифференцируемые поверхности.

Def. Поверхность является — гладкой (регулярной) поверхностью, если среди её параметризации найдется такая параметризация r = r(u,v), что вектор-функция r(u,v) – n раз непрерывно диффенцируема и в каждой точке (u,v) её первые частные производные (u,v) и (u,v) неколлинеарны.

3) Кривые на поверхности. Координатные линии.

Рассмотрим в пространстве поверхность Ф заданную гладкой параметризацией r = r(u,v). Вектор-функция r(u,v) определена в области D переменных u и v.

Если в области D выбрать кривую , то её образом будет кривая на поверхности Ф. Кривую в D можно задать параметрически: тогда

Замечание 1. Уравнения называются внутренними уравнениями кривой на поверхности Ф.

Замечание 2. Если в качестве внутренних уравнений взять семейства кривых:

координатная сеть на множестве D, то они определяют координатные линии на поверхности Ф.

4) Касательная плоскость к поверхности Ф.

Def. Под касательной плоскостью к любой поверхности в данной точке будем понимать плоскость, которая содержит все касательные прямые к кривым, лежащим на поверхности и проходящим через выбранную точку. Это определение подтверждает следующее:

Теорема. Пусть Ф – гладкая поверхность, вектор-функция r(u,v) определенная на D её гладкая параметризация. Точка плоскость, проходящая через т. х и имеющие векторы своими направляющими векторами. Тогда все касательные прямые в т. х к гладким кривым, лежащим на поверхности Ф и проходящим через т. х, содержаться в плоскости и заполняют

Из теоремы следует, что векторы R – r, компланарные векторное уравнение касательной плоскости или через координаты:

=0.

В случае явного задания поверхности:

=0 или

В случае неявного задания поверхности:

5) Нормаль к поверхности и её уравнение.

Определение. Прямая, проведенная через заданную точку поверхности и ортогональная касательной плоскости поверхности проведенной через эту же точку поверхности, называется нормалью к поверхности в данной точке.

Замечание. Иногда называют вектор касательной плоскости в данной точке.

Уравнение нормали: , где координаты вектора

В этом случае: а) для явного задания поверхности:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 7702 — | 6713 — или читать все.

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

ПОНЯТИЕ ПОВЕРХНОСТИ

Элементарная поверхность. Простая поверхность. Общая поверхность

Поверхность, одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.

В школьном курсе геометрии рассматриваются плоскости, многогранники, а также некоторые кривые поверхности. Каждая из кривых поверхностей определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, поверхность шара — множество точек, отстоящих на заданном расстоянии от данной точки. Понятие «Поверхность» лишь поясняется, а не определяется. Например, говорят, что поверхность есть граница тела или след движущейся линии.

Математически строгое определение поверхности основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). Более точно, простой поверхностью называется образ гомеоморфного отображения (т. е. взаимно однозначного и взаимно непрерывного отображения) внутренности квадрата.

В дифференциальной геометрии, исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, т. е. существования в каждой точке поверхности определённой касательной плоскости, кривизны и т.д.

В аналитической геометрии и в алгебраической геометрии поверхность определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений: .

Таким образом, определённая поверхность может и не иметь наглядного геометрического образа. В этом случае для сохранения общности говорят о мнимых поверхностях. Например, уравнение мнимой сферы, хотя в действительном пространстве нет ни одной точки, координаты которой удовлетворяют ее уравнению. Если функция непрерывна в некоторой точке и имеет в ней непрерывные частные производные , из которых хотя бы одна не обращается в нуль, то в окрестности этой точки поверхности, заданная уравнением , будет правильной поверхностью.

Понятие поверхности, интуитивно достаточно ясное, можно определять с различной степенью общности. В анализе чаще всего приходится рассматривать поверхности, задаваемые уравнениями вида

где — непрерывная функция, определенная в некоторой области . Несколько более широкий класс поверхностей мы получим, рассматривая уравнения вида

Чтобы такое уравнение действительно определяло поверхность (в смысле, соответствующем нашим наглядным представлениям), необходимо на функцию наложить некоторые дополнительные условия.

Область на плоскости мы будем называть элементарной областью, если она является образом открытого круга при топологическом отображении. Таким образом, элементарная область — это область гомеоморфная кругу.

Пусть — простая замкнутая кривая на плоскости. По теореме Жордана: Простая замкнутая кривая разбивает плоскость на две области и является границей для каждой из областей. Одна из областей конечна, другая — бесконечна. Оказывается, конечная область гомеоморфна кругу. Таким образом, внутренность квадрата, прямоугольника, внутренность эллипса — все это элементарные области.

Определим элементарную поверхность.

Пусть — множество в евклидовом пространстве . Множество называется элементарной поверхностью, если при проекции на некоторую плоскость оно взаимно однозначно и взаимно непрерывно отображается на открытую область в этой плоскости.

Примеры. Любая плоская область является элементарной поверхностью.

Сфера не является элементарной поверхностью, хотя таковой будет всякая достаточно малая сферическая область.

Если мы фиксируем плоскость, фигурирующую в определении элементарной поверхности, то получим возможность явно задать элементарную поверхность . Пусть — рассматриваемая плоскость. Введем в пространстве декартову систему координат так, чтобы плоскость совпадала с координатной плоскостью . Тогда проекция на плоскость точки с координатами будет иметь координаты . Если область — образ элементарной поверхности при проекции на , то множество будет графиком некоторой непрерывной функции , определенной в области . Поэтому множество можно задать уравнением

Такое задание называется явным, а само уравнение называется уравнением элементарной поверхности в явном виде.

Для многих целей элементарную поверхность удобно рассматривать как образ области при ее отображении в пространство , которое точке с координатами ставит в соответствие точку с координатами .

Множество точек пространства мы будем называть простой поверхностью, если это множество связно и каждая точка этого множества имеет окрестность такую, что часть , расположенная в , является элементарной поверхностью.

Элементарная поверхность является простой поверхностью. Но элементарными поверхностями далеко не исчерпываются все простые поверхности. Например, сфера является простой поверхностью, но не элементарной. Простые поверхности нельзя в целом охарактеризовать в целом общо и просто, как это можно сделать для простых кривых. Некоторое представление о разнообразии простых поверхностей дает следующее сообщение. Если из произвольной простой поверхности удалить любое замкнутое множество точек, но так, чтобы не нарушать связности оставшейся части, то эта оставшаяся часть будет также простой поверхностью.

Простая поверхность называется полной, если предельная точка для любой сходящейся последовательности точек поверхности также является точкой поверхности. Например, сфера, параболоид суть полные поверхности, а сферический сегмент не является полной поверхностью (речь идет о сферическом сегменте без ограничивающей его окружности).

Если простая полная поверхность является конечной, то она называется замкнутой. Кроме сферы, замкнутой поверхностью является, например, тор — поверхность, получаемая вращением окружности около прямой, лежащей в области окружности и не пересекающей окружность (Рисунок 1.).