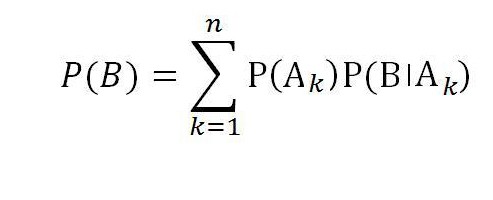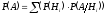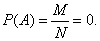Определение события с точки зрения теории вероятности

Многие, столкнувшись с понятием «теория вероятности», пугаются, думая, что это нечто непосильное, очень сложное. Но все на самом деле не так трагично. Сегодня мы рассмотрим основное понятие теории вероятности, научимся решать задачи на конкретных примерах.

Что же изучает такой раздел математики, как «теория вероятности»? Она отмечает закономерности случайных событий и величин. Впервые данным вопросом заинтересовались ученые еще в восемнадцатом веке, когда изучали азартные игры. Основное понятие теории вероятности – событие. Это любой факт, который констатируется опытом или наблюдением. Но что же такое опыт? Еще одно основное понятие теории вероятности. Оно означает, что этот состав обстоятельств создан не случайно, а с определенной целью. Что касается наблюдения, то здесь исследователь сам не участвует в опыте, а просто является свидетелем данных событий, он никак не влияет на происходящее.

Мы узнали, что основное понятие теории вероятности – это событие, но не рассмотрели классификацию. Все они делятся на следующие категории:

Независимо от того, какие это события, за которыми наблюдают или создают в ходе опыта, все они подвержены данной классификации. Предлагаем с каждым из видов познакомиться отдельно.

Достоверное событие

Это такое обстоятельство, перед которым сделан необходимый комплекс мероприятий. Для того чтобы лучше вникнуть в суть, лучше привести несколько примеров. Этому закону подчинены и физика, и химия, и экономика, и высшая математика. Теория вероятности включает такое важное понятие, как достоверное событие. Приведем примеры:

• Мы работаем и получаем вознаграждение в виде заработной платы.
• Сдали хорошо экзамены, прошли конкурс, за это получаем вознаграждение в виде поступления в учебное заведение.
• Мы вложили деньги в банк, при необходимости получим их назад.

Такие события являются достоверными. Если мы выполнили все необходимые условия, то обязательно получим ожидаемый результат.

Невозможные события

Сейчас мы рассматриваем элементы теории вероятности. Предлагаем перейти к пояснению следующего вида события, а именно — невозможного. Для начала оговорим самое важное правило – вероятность невозможного события равна нулю.

От данной формулировки нельзя отступать при решении задач. Для пояснения приведем примеры таких событий:

• Вода замерзла при температуре плюс десять (это невозможно).
• Отсутствие электроэнергии никак не влияет на производство (так же невозможно, как и в предыдущем примере).

Более примеров приводить не стоит, так как описанные выше очень ярко отражают суть данной категории. Невозможное событие никогда не произойдет во время опыта ни при каких обстоятельствах.

Случайные события

Изучая элементы теории вероятности, особое внимание стоит уделить именно данному виду события. Именно их и изучает данная наука. В результате опыта может что-то произойти или нет. Кроме этого, испытание может проводиться неограниченное количество раз. Яркими примерами могут служить:

• Бросок монеты – это опыт, или испытание, выпадение орла – это событие.
• Вытягивание мячика из мешка вслепую – испытание, попался красный шар – это событие и так далее.

Таких примеров может быть неограниченное количество, но, в общем, суть должна быть понятна. Для обобщения и систематизирования полученных знаний о событиях приведена таблица. Теория вероятности изучает только последний вид из всех представленных.

События, происходящие со стопроцентной гарантией при соблюдении некоторых условий.

Поступление в учебное заведение при хорошей сдаче вступительного экзамена.

События, которые никогда не произойдут ни при каких условиях.

Идет снег при температуре воздуха плюс тридцать градусов по Цельсию.

Событие, которое может произойти или нет в ходе проведения опыта/испытания.

Попадание или промах при бросании баскетбольного мяча в кольцо.

Теория вероятности – это наука, изучающая возможность выпадения какого-либо события. Как и другие, она имеет некоторые правила. Существуют следующие законы теории вероятности:

• Сходимость последовательностей случайных величин.
• Закон больших чисел.

При расчете возможности сложного можно использовать комплекс простых событий для достижения результата более легким и быстрым путем. Отметим, что законы теории вероятности легко доказываются с помощью некоторых теорем. Предлагаем для начала познакомиться с первым законом.

Сходимость последовательностей случайных величин

Отметим, что видов сходимости несколько:

• Последовательность случайных величин сходима по вероятности.
• Почти невозможное.
• Среднеквадратическая сходимость.
• Сходимость по распределению.

Так, с лету, очень тяжело вникнуть в суть. Приведем определения, которые помогут разобраться в данной теме. Для начала первый вид. Последовательность называют сходимой по вероятности, если соблюдено следующее условие: n стремится к бесконечности, число, к которому стремится последовательность, больше нуля и приближена к единице .

Переходим к следующему виду, почти наверное. Говорят, что последовательность сходится почти наверное к случайной величине при n, стремящейся к бесконечности, и Р, стремящейся к величине, приближенной к единице.

Следующий тип – это сходимость среднеквадратическая. При использовании СК-сходимости изучение векторных случайных процессов сводится к изучению их координатных случайных процессов.

Остался последний тип, давайте разберем кратко и его, чтобы переходить непосредственно к решению задач. Сходимость по распределению имеет и еще одно название — «слабое», далее поясним, почему. Слабая сходимость — это сходимость функций распределения во всех точках непрерывности предельной функции распределения.

Обязательно выполним обещание: слабая сходимость отличается от всех вышеперечисленных тем, что случайная величина не определена на вероятностном пространстве. Это возможно потому, что условие формируется исключительно с использованием функций распределения.

Закон больших чисел

Отличными помощниками при доказательстве данного закона станут теоремы теории вероятности, такие как:

• Неравенство Чебышева.
• Теорема Чебышева.
• Обобщенная теорема Чебышева.
• Теорема Маркова.

Если будем рассматривать все эти теоремы, то данный вопрос может затянуться на несколько десятков листов. У нас же основная задача – это применение теории вероятности на практике. Предлагаем вам прямо сейчас этим и заняться. Но перед этим рассмотрим аксиомы теории вероятностей, они будут основными помощниками при решении задач.

С первой мы уже познакомились, когда говорили о невозможном событии. Давайте вспоминать: вероятность невозможного события равна нулю. Пример мы приводили очень яркий и запоминающийся: выпал снег при температуре воздуха тридцать градусов по Цельсию.

Вторая звучит следующим образом: достоверное событие происходит с вероятностью, равной единице. Теперь покажем, как это записать с помощью математического языка: Р(В)=1.

Третья: Случайное событие может произойти или нет, но возможность всегда варьируется в пределах от нуля до единицы. Чем ближе значение к единице, тем шансов больше; если значение приближается к нулю, вероятность очень мала. Запишем это математическим языком: 0 18 ноября, 2016

Вероятность события. Определение вероятности события

Изначально, будучи всего лишь собранием сведений и эмпирических наблюдений за игрой в кости, теория вероятности стала основательной наукой. Первыми, кто придал ей математический каркас, были Ферма и Паскаль.

От размышлений о вечном до теории вероятностей

Две личности, которым теория вероятностей обязана многими фундаментальными формулами, Блез Паскаль и Томас Байес, известны как глубоко верующие люди, последний был пресвитерианским священником. Видимо, стремление этих двух ученых доказать ошибочность мнения о некой Фортуне, дарующей удачу своим любимчикам, дало толчок к исследованиям в этой области. Ведь на самом деле любая азартная игра с ее выигрышами и проигрышами — это всего лишь симфония математических принципов.

Благодаря азарту кавалера де Мере, который в равной степени был игроком и человеком небезразличным к науке, Паскаль вынужден был найти способ расчета вероятности. Де Мере интересовал такой вопрос: «Сколько раз нужно выбрасывать попарно две кости, чтобы вероятность получить 12 очков превышала 50%?». Второй вопрос, крайне интересовавший кавалера: «Как разделить ставку между участниками незаконченной игры?» Разумеется, Паскаль успешно ответил на оба вопроса де Мере, который стал невольным зачинателем развития теории вероятностей. Интересно, что персона де Мере так и осталась известна в данной области, а не в литературе.

Ранее ни один математик еще не делал попыток вычислять вероятности событий, поскольку считалось, что это лишь гадательное решение. Блез Паскаль дал первое определение вероятности события и показал, что это конкретная цифра, которую можно обосновать математическим путем. Теория вероятностей стала основой для статистики и широко применяется в современной науке.

Что такое случайность

Если рассматривать испытание, которое можно повторить бесконечное число раз, тогда можно дать определение случайному событию. Это один из вероятных исходов опыта.

Опытом является осуществление конкретных действий в неизменных условиях.

Чтобы можно было работать с результатами опыта, события обычно обозначают буквами А, B, C, D, Е…

Вероятность случайного события

Чтобы можно было приступить к математической части вероятности, нужно дать определения всем ее составляющим.

Вероятность события – это выраженная в числовой форме мера возможности появления некоторого события (А или B) в результате опыта. Обозначается вероятность как P(A) или P(B).

В теории вероятностей отличают:

• достоверное событие гарантированно происходит в результате опыта Р(Ω) = 1;
• невозможное событие никогда не может произойти Р(Ø) = 0;
• случайное событие лежит между достоверным и невозможным, то есть вероятность его появления возможна, но не гарантирована (вероятность случайного события всегда в пределах 0≤Р(А)≤ 1).

Отношения между событиями

Рассматривают как одно, так и сумму событий А+В, когда событие засчитывается при осуществлении хотя бы одного из составляющих, А или В, или обоих – А и В.

По отношению друг к другу события могут быть:

• Равновозможными.
• Совместимыми.
• Несовместимыми.
• Противоположными (взаимоисключающими).
• Зависимыми.

Если два события могут произойти с равной вероятностью, то они равновозможные.

Если появление события А не сводит к нулю вероятность появление события B, то они совместимые.

Если события А и В никогда не происходят одновременно в одном и том же опыте, то их называют несовместимыми. Бросание монеты — хороший пример: появление решки – это автоматически непоявление орла.

Вероятность для суммы таких несовместимых событий состоит из суммы вероятностей каждого из событий:

Если наступление одного события делает невозможным наступление другого, то их называют противоположными. Тогда одно из них обозначают как А, а другое – Ā (читается как «не А»). Появление события А означает, что Ā не произошло. Эти два события формируют полную группу с суммой вероятностей, равной 1.

Зависящие события имеют взаимное влияние, уменьшая или увеличивая вероятность друг друга.

Отношения между событиями. Примеры

На примерах гораздо проще понять принципы теории вероятностей и комбинации событий.

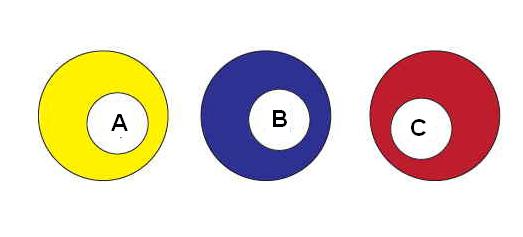
Опыт, который будет проводиться, заключается в вытаскивании шариков из ящика, а результата каждого опыта – элементарный исход.

Событие – это один из возможных исходов опыта – красный шар, синий шар, шар с номером шесть и т. д.

Испытание №1. Участвуют 6 шаров, три из которых окрашены в синий цвет, на них нанесены нечетные цифры, а три других – красные с четными цифрами.

Испытание №2. Участвуют 6 шаров синего цвета с цифрами от одного до шести.

Исходя из этого примера, можно назвать комбинации:

• Достоверное событие. В исп. №2 событие «достать синий шар» достоверное, поскольку вероятность его появления равна 1, так как все шары синие и промаха быть не может. Тогда как событие «достать шар с цифрой 1» – случайное.
• Невозможное событие. В исп. №1 с синими и красными шарами событие «достать фиолетовый шар» невозможное, поскольку вероятность его появления равна 0.
• Равновозможные события. В исп. №1 события «достать шар с цифрой 2» и «достать шар с цифрой 3» равновозможные, а события «достать шар с четным числом» и «достать шар с цифрой 2» имеют разную вероятность.
• Совместимые события. Два раза подряд получить шестерку в процессе бросания игральной кости – это совместимые события.
• Несовместимые события. В том же исп. №1 события «достать красный шар» и «достать шар с нечетным числом» не могут быть совмещены в одном и том же опыте.
• Противоположные события. Наиболее яркий пример этого – подбрасывание монет, когда вытягивание орла равносильно невытягиванию решки, а сумма их вероятностей – это всегда 1 (полная группа).
• Зависимые события. Так, в исп. №1 можно задаться целью извлечь два раза подряд красный шар. Его извлечение или неизвлечение в первый раз влияет на вероятность извлечения во второй раз.

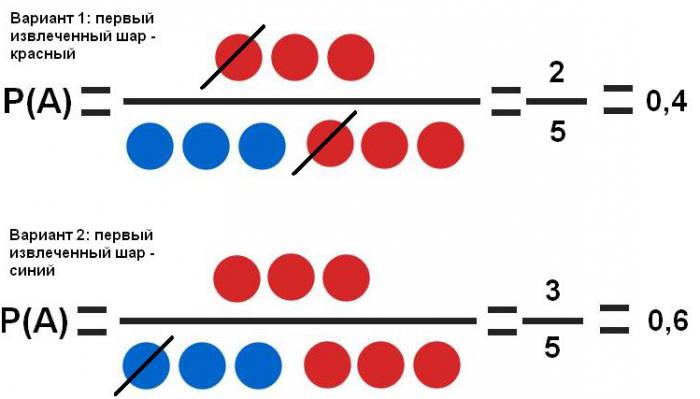
Видно, что первое событие существенно влияет на вероятность второго (40% и 60%).

Формула вероятности события

Переход от гадательных размышлений к точным данным происходит посредством перевода темы в математическую плоскость. То есть суждения о случайном событии вроде «большая вероятность» или «минимальная вероятность» можно перевести к конкретным числовым данным. Такой материал уже допустимо оценивать, сравнивать и вводить в более сложные расчеты.

С точки зрения расчета, определение вероятности события – это отношение количества элементарных положительных исходов к количеству всех возможных исходов опыта относительно определенного события. Обозначается вероятность через Р(А), где Р означает слово «probabilite», что с французского переводится как «вероятность».

Итак, формула вероятности события:

Где m – количество благоприятных исходов для события А, n – сумма всех исходов, возможных для этого опыта. При этом вероятность события всегда лежит между 0 и 1:

Расчет вероятности события. Пример

Возьмем исп. №1 с шарами, которое описано ранее: 3 синих шара с цифрами 1/3/5 и 3 красных с цифрами 2/4/6.

На основании этого испытания можно рассматривать несколько разных задач:

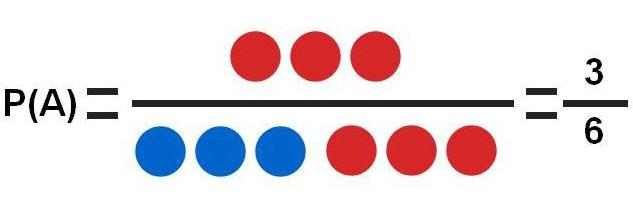
• A – выпадение красного шара. Красных шаров 3, а всего вариантов 6. Это простейший пример, в котором вероятность события равна Р(А)=3/6=0,5.
• B – выпадение четного числа. Всего четных чисел 3 (2,4,6), а общее количество возможных числовых вариантов – 6. Вероятность этого события равна Р(B)=3/6=0,5.
• C – выпадение числа, большего, чем 2. Всего таких вариантов 4 (3,4,5,6) из общего количества возможных исходов 6. Вероятность события С равна Р(С)=4/6=0,67.

Как видно из расчетов, событие С имеет большую вероятность, поскольку количество вероятных положительных исходов выше, чем в А и В.

Несовместные события

Такие события не могут одновременно появиться в одном и том же опыте. Как в исп. №1 невозможно одновременно достать синий и красный шар. То есть можно достать либо синий, либо красный шар. Точно так же в игральной кости не могут одновременно появиться четное и нечетное число.

Вероятность двух событий рассматривается как вероятность их суммы или произведения. Суммой таких событий А+В считается такое событие, которое состоит в появлении события А или В, а произведение их АВ – в появлении обоих. Например, появление двух шестерок сразу на гранях двух кубиков в одном броске.

Сумма нескольких событий являет собой событие, предполагающее появление, по крайней мере, одного из них. Произведение нескольких событий – это совместное появление их всех.

В теории вероятности, как правило, употребление союза «и» обозначает сумму, союза «или» – умножение. Формулы с примерами помогут понять логику сложения и умножения в теории вероятностей.

Вероятность суммы несовместных событий

Если рассматривается вероятность несовместных событий, то вероятность суммы событий равна сложению их вероятностей:

Например: вычислим вероятность того, что в исп. №1 с синими и красными шарами выпадет число между 1 и 4. Рассчитаем не в одно действие, а суммой вероятностей элементарных составляющих. Итак, в таком опыте всего 6 шаров или 6 всех возможных исходов. Цифры, которые удовлетворяют условие, – 2 и 3. Вероятность выпадения цифры 2 составляет 1/6, вероятность цифра 3 также 1/6. Вероятность того, что выпадет цифра между 1 и 4 равна:

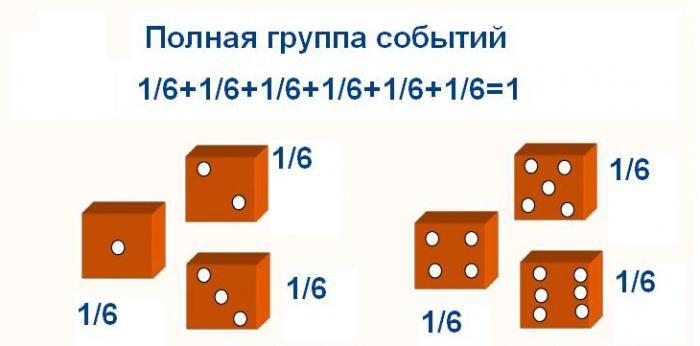
Вероятность суммы несовместимых событий полной группы равна 1.

Так, если в опыте с кубиком сложить вероятности выпадения всех цифр, то в результате получим единицу.

Также это справедливо для противоположных событий, например в опыте с монетой, где одна ее сторона – это событие А, а другая – противоположное событие Ā, как известно,

Вероятность произведения несовместных событий

Умножение вероятностей применяют, когда рассматривают появление двух и более несовместных событий в одном наблюдении. Вероятность того, что в нем появятся события A и B одновременно, равна произведению их вероятностей, или:

Например, вероятность того, что в исп. №1 в результате двух попыток два раза появится синий шар, равна

То есть вероятность наступления события, когда в результате двух попыток с извлечением шаров будет извлечены только синие шары, равна 25%. Очень легко проделать практические эксперименты этой задачи и увидеть, так ли это на самом деле.

Совместные события

События считаются совместными, когда появление одного из них может совпасть с появлением другого. Несмотря на то что они совместные, рассматривается вероятность независимых событий. К примеру, бросание двух игральных костей может дать результат, когда на обеих из них выпадает цифра 6. Хотя события совпали и появились одновременно, они независимы друг от друга – могла выпасть всего одна шестерка, вторая кость на нее влияния не имеет.

Вероятность совместных событий рассматривают как вероятность их суммы.

Вероятность суммы совместных событий. Пример

Вероятность суммы событий А и В, которые по отношению к друг другу совместные, равняется сумме вероятностей события за вычетом вероятности их произведения (то есть их совместного осуществления):

Допустим, что вероятность попадания в мишень одним выстрелом равна 0,4. Тогда событие А – попадание в мишень в первой попытке, В – во второй. Эти события совместные, поскольку не исключено, что можно поразить мишень и с первого, и со второго выстрела. Но события не являются зависимыми. Какова вероятность наступления события поражения мишени с двух выстрелов (хотя бы с одного)? Согласно формуле:

Ответ на вопрос следующий: «Вероятность попасть в цель с двух выстрелов равна 64%».

Эта формула вероятности события может быть применима и к несовместным событиям, где вероятность совместно появления события Р(АВ) = 0. Это значит, что вероятность суммы несовместных событий можно считать частным случаем предложенной формулы.

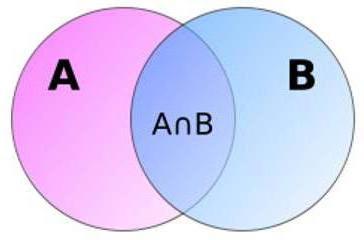
Геометрия вероятности для наглядности

Интересно, что вероятность суммы совместных событий может быть представлена в виде двух областей А и В, которые пересекаются между собой. Как видно из картинки, площадь их объединения равна общей площади за минусом области их пересечения. Это геометрическое пояснения делают более понятной нелогичную на первый взгляд формулу. Отметим, что геометрические решения – не редкость в теории вероятностей.

Определение вероятности суммы множества (больше двух) совместных событий довольно громоздкое. Чтобы вычислить ее, нужно воспользоваться формулами, которые предусмотрены для этих случаев.

Зависимые события

Зависимыми события называются в случае, если наступление одного (А) из них влияет на вероятность наступления другого (В). Причем учитывается влияние как появления события А, так и его непоявление. Хотя события и называются зависимыми по определению, но зависимо лишь одно из них (В). Обычная вероятность обозначалась как Р(В) или вероятность независимых событий. В случае с зависимыми вводится новое понятие – условная вероятность Р_A(В) , которая является вероятностью зависимого события В при условии произошедшего события А (гипотезы), от которого оно зависит.

Но ведь событие А тоже случайно, поэтому у него также есть вероятность, которую нужно и можно учитывать в осуществляемых расчетах. Далее на примере будет показано, как работать с зависимыми событиями и гипотезой.

Пример расчета вероятности зависимых событий

Хорошим примером для расчета зависимых событий может стать стандартная колода карт.

На примере колоды в 36 карт рассмотрим зависимые события. Нужно определить вероятность того, что вторая карта, извлеченная из колоды, будет бубновой масти, если первая извлеченная:

Очевидно, что вероятность второго события В зависит от первого А. Так, если справедлив первый вариант, что в колоде стало на 1 карту (35) и на 1 бубну (8) меньше, вероятность события В:

Если же справедлив второй вариант, то в колоде стало 35 карт, и по-прежнему сохранилось полное число бубен (9), тогда вероятность следующего события В:

Видно, что если событие А условлено в том, что первая карта – бубна, то вероятность события В уменьшается, и наоборот.

Умножение зависимых событий

Руководствуясь предыдущей главой, мы принимаем первое событие (А) как факт, но если говорить по сути, оно имеет случайный характер. Вероятность этого события, а именно извлечение бубны из колоды карт, равна:

Поскольку теория не существует сама по себе, а призвана служить в практических целях, то справедливо отметить, что чаще всего нужна вероятность произведения зависимых событий.

Согласно теореме о произведении вероятностей зависимых событий, вероятность появления совместно зависимых событий А и В равна вероятности одного события А, умноженная на условную вероятность события В (зависимого от А):

Тогда в примере с колодой вероятность извлечения двух карт с мастью бубны равна:

9/36*8/35=0,0571, или 5,7%

И вероятность извлечения вначале не бубны, а потом бубны, равна:

27/36*9/35=0,19, или 19%

Видно, что вероятность появления события В больше при условии, что первой извлекается карта масти, отличной от бубны. Такой результат вполне логичный и понятный.

Полная вероятность события

Когда задача с условными вероятностями становится многогранной, то обычными методами ее вычислить нельзя. Когда гипотез больше двух, а именно А1,А2,…,А_n, ..образует полную группу событий при условии:

Итак, формула полной вероятности для события В при полной группе случайных событий А1,А2,…,А_n равна_:

Взгляд в будущее

Вероятность случайного события крайне необходима во многих сферах науки: эконометрике, статистике, в физике и т. д. Поскольку некоторые процессы невозможно описать детерминировано, так как они сами имеют вероятностный характер, необходимы особые методы работы. Теория вероятности события может быть использована в любой технологичной сфере как способ определить возможность ошибки или неисправности.

Можно сказать, что, узнавая вероятность, мы некоторым образом делаем теоретический шаг в будущее, разглядывая его через призму формул.

Вопросы и задачи к модулю «основы биологической физики» для студентов 1 курса всех факультетов на 1 семестр тема: Элементы теории вероятностей.

Сформулируйте определение события с точки зрения теории вероятностей.

Что называют абсолютной частотой случайного события?

* Предел, к которому стремится относительная частота события при числе опытов, стремящихся к бесконечности

Что называют относительной частотой событий?

* Отношение общего числа опытов к числу испытаний, которые благоприятствуют наступлению интересующего события

Дайте определение случайного события.

* Которое может произойти, но может и не произойти в результате данного опыта

Дайте определение достоверного события.

* Которое обязательно наступит в результате испытания

Дайте определение невозможного события.

* Никогда не может произойти в результате данного опыта

Чему равна вероятность достоверного события?

Чему равна вероятность невозможного события?

Какие события называются совместными?

* Которые могут наступать одновременно в результате данного испытания.

Какие события называются несовместными?

* Которые никогда не могут наступать одновременно в результате данного опыта

Какие события называются зависимыми?

* Зависимыми называются события А и В, если вероятность наступления события В изменяется в зависимости от того, произошло ли событие А

Какие события называются независимыми?

* Независимыми называются события А и В, если вероятность наступления события В не изменяется в зависимости от того, произошло ли событие А

Какие события называются противоположными?

* Под противоположным событием понимается событие Ā, которое обязательно должно произойти, если не наступило некоторое событие А

Чему равна сумма вероятностей противоположных событий?

Какие события образуют полную группу несовместных событий?

* Которые несовместны и в результате каждого испытания появляется только одно из этих событий

Чему равна сумма вероятностей событий, которые образуют полную группу событий?

Сформулируйте классическое определение вероятности случайного события.

* Отношение благоприятствующих случаев к общему числу равновозможных совместных событий

Сформулируйте статистическое определение вероятности случайного события.

* Предел, к которому стремится относительная частота встречаемости событий при неограниченном увеличении числа испытаний

Дайте определение условной вероятности

* События В при условии, что событие А состоялось

Как записывается формула теоремы сложения вероятностей?

Сформулируйте теорему сложения вероятностей.

*Вероятность появления одного из нескольких несовместных событий (А или В) равнаР(А)+Р(В)

В каких случаях применяется теорема сложения вероятностей?

* Когда необходимо рассчитать вероятность одновременного появления нескольких независимых событий

23. Сформулируйте теорему умножения вероятностей для независимых событий.

* Вероятность одновременного появления в результате опыта двух и более независимых событий равна произведению вероятностей этих событий

24. Как записывается формула теоремы умножения вероятностей для независимых событий?

25. В каких случаях применяется теорема умножения вероятностей для независимых событий?

* Когда требуется вычеслить вероятность одновременного появления нескольких независимых событий

26. Сформулируйте теорему умножения вероятностей для зависимых событий.

* Вероятность совместного появления в результате опыта двух (или более) зависимых событий равна произведению вероятности первого события на условную вероятность второго (третьего и т.д.)

Сформулируйте теорему умножения вероятностей для независимых событий.

* Вероятность одновременного появления в результате опыта двух и более независимых событий равна произведению вероятностей этих событий

В каких случаях применяется теорема умножения вероятностей для независимых событий?

*Когда требуется вычислить вероятность одновременного появления нескольких независимых событий

Как записывается формула теоремы умножения вероятностей для зависимых событий?

В каких случаях применяется теорема умножения вероятностей для зависимых событий?

* Когда необходимо рассчитать вероятность одновременного появления нескольких зависимых событий

Как записывается формула теоремы полной вероятности?

*

В каких случаях применяется формула полной вероятности?

* Когда событие А наст только при усл появления одного из событий образующих полн группу

В каких случаях применяется формула Байеса?

* Когда событие А появляющееся совместно с каким-либо из событий образующих полную группу произошло и требуется произвести количественную переоценку вероятностей гипотез В_1, В_2, В_n.

Понятие вероятности события

Основными понятиями теории вероятностей являются понятия события и вероятности события.

Событием будем называть любое утверждение, которое может как произойти, так и не произойти.

Обычно события обозначаются большими английскими буквами.

Пример: $A$ – выпадение числа $6$ на кости.

В связи с тем, что событие может иметь две вариации исхода («произошло» и «не произошло») мы сталкиваемся с понятие вероятности такого события.

Понятие вероятности события

Вероятностью события будем называть число, которое обозначает степень возможности, что такое событие произойдет.

Вероятность события обозначается как $P(A)$

Чтобы определить границы значения этого числа введем понятие достоверного и невозможного событий.

Достоверным событием будем называть такое, которое произойдет при любых обстоятельствах.

Примером такого события может быть следующее: Сумма «точек» на классической кости всегда равняется $21$.

Вероятность такого события мы будем принимать за единицу.

Попробуй обратиться за помощью к преподавателям

Невозможным событием будем называть такое, которое не может произойти ни при каком обстоятельстве.

Примером такого события может быть следующее: При игре в «очко» игрок набрал $1$ очко.

Вероятность такого события мы будем принимать за $0$.

То есть значение вероятности любого события содержится в отрезке $[0,1]$.

В современной теории вероятности принято выделять четыре определения для вероятности: классической, геометрическое, статистическое и аксиоматическое определения. Рассмотрим их отдельно.

Классическое определение

Классическое определение связано с такими неопределяемыми понятиями как равновозможность и элементарность события. Интуитивно их можно понять на следующих примерах:

Равновозможность: При подбрасывании монеты она может упасть как аверсом, так и реверсом независимо от внешних условий. То есть можно сказать что вероятность выпадения одной или другой стороны по сути одинакова.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Элементарность события: Если на кости выпадет число $4$, то это означает, что числа $1, 2, 3, 5$ и $6$ уже не выпали.

Вероятностью события будем называть отношения числа n равновозможных элементарных событий исходного события $B$ ко всем элементарным событиям $N$.

Математически это выглядит следующим образом:

Геометрическое определение

Геометрическое определение применяется для случая, когда количество равновозможных событий будет бесконечно. Здесь, для введения геометрического определения рассмотрим следующий пример. Для игры дартс берем круг площадью $S$ и разбиваем его на несколько кругов. Какова вероятность, что дротик попадет в центральный круг? (Исключим здесь случаи полного непопадания в поле). Очевидно что равновозможных событий здесь будет бесконечно (как и общих событий) так как круг содержит в себе бесконечное число точек. Пусть площадь центрального круга равняется $s$. Тогда мы сталкиваемся с геометрическим определением вероятности такого события:

Статистическое (частотное) определение

Классическое определение довольно часто не учитывает всех возможностей. Рассматривая даже классический пример с бросанием кости мы пренебрегаем возможностью, что не выпадет никакого из шести чисел (кубик просто «остановится» на уголке). Поэтому вводят следующее определение вероятности, учитывающее все возможности. Рассматриваем $N$ наблюдений. Пусть нужное нам событие при этом выпало $n$ раз. Тогда

Аксиоматическое определение

Данное определение задается с помощью аксиоматики Колмогорова.

Пусть $X$ — пространство всех элементарных событий. Тогда

Вероятностью события $B$ будем называть такую функцию $P(B)$, которая удовлетворяет следующим условиям:

1. Данная функция всегда неотрицательна,
2. Вероятность того, что произойдет хотя бы одно из попарно несовместных событий равняется сумме их вероятностей.
3. Функция всегда меньше или равна $1$, причем $P(X)=1$.

Примеры задач

Найти вероятность того, что наугад вытащенная из колоды карт будет бубновой масти (сумма карт в колоде кратна $4$-м).

Решение.

Так как количество карт кратно четверке, то пусть всего карт будет $4k$. Тогда каждой масти карт будет $k$ штук (так как мастей $4$ и их количество одинаково).

При решении этой задачи будем использовать определение $5$. Во введенных нами обозначениях, получим что в определении $5$ мы будем иметь

Ответ: $\frac$.

Пусть нам дана точка $(a,b)$, где $-5

Тут мы будем использовать геометрическое определение. Изобразим вначале область, в которую в принципе может попасть эта точка (рис. 1).

Из этого рисунка видим, что

$S=8\cdot 5=40,s=3\cdot 3=9$

Тогда из геометрического определения:

$P=\frac$ Ответ: $\frac$.

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Понятие события и его вероятности

Предмет теории вероятности

математический вероятность бейес производная

Математическая наука, изучающая общие закономерности случайных массовых явлений независимо от их конкретной природы и дающая методы количественной оценки влияния различных случайных факторов на рассматриваемые явления называется теорией вероятностей.

На основе наблюдений и опыта наука приходит к формулировке закономерностей, которым подчиняется течение изучаемых ею явлений. Простейшая и наиболее распространенная схема устанавливаемых закономерностей такова:

Предложение 1. При каждом осуществлении определенного комплекса условий происходит событие А.

Так, например, если вода при атмосферном давлении в 760 мм нагревается выше 100° по Цельсию (комплекс условий), то она превращается в пар (событие А). Или другой пример: при любых химических реакциях каких угодно веществ, без обмена с окружающей средой (комплекс условий) общее количество вещества (материи) остается неизменным (событие А). Последнее утверждение носит название закона сохранения материи. Читатель легко может самостоятельно указать примеры других подобных закономерностей, заимствованных из физики, химии, биологии и других наук.

Определение 1.Событие, которое неизбежно происходит при каждой реализации комплекса условий, называется достоверным.

Определение 2.Если событие A заведомо не может произойти при осуществлении комплекса условий, то оно называется невозможным.

Определение 3. Событие А, которое при реализации комплекса условий может произойти, а может и не произойти, называется случайным.

Из этих определений ясно, что, говоря о достоверности, невозможности, случайности какого-либо события, мы всегда будем иметь в виду его достоверность, невозможность или случайность по отношению к какому-либо определенному комплексу условий.

Простое утверждение о случайности события имеет очень ограниченный познавательный интерес: оно сводится лишь к указанию на то, что комплекс условий не отражает всей совокупности причин, необходимых и достаточных для появления события А. Такое указание нельзя считать совершенно бессодержательным, так как оно может послужить стимулом к дальнейшему изучению условий появления события А, но само по себе оно еще не дает нам положительного знания.

Имеется, однако, широкий круг явлений, когда при многократном осуществлении комплекса условий доля той части случаев, когда событие А происходит, лишь изредка уклоняется сколько-нибудь значительно от некоторой средней цифры, которая, таким образом, может служить характерным показателем массовой операции, (многократного повторения комплекса) по отношению к событию A.

Для указанных явлений возможно не только простое констатирование случайности события А, но и количественная оценка возможности его появления. Эта оценка выражается предложением вида:

Предложение 2. Вероятность того, что при осуществлении комплекса условий произойдет событие А, равна р.

Закономерности этого второго рода называются вероятностными или стохастическими закономерностями. Вероятностные закономерности играют большую роль в самых различных областях науки.

Несомненно, что понятие математической вероятности заслуживает углубленного философского изучения. И основная специфическая философская проблема, выдвигаемая самим существованием теории вероятностей и успешным ее применением к реальным явлениям, состоит в следующем: при каких условиях имеет объективный смысл количественная оценка вероятности случайного события А при помощи определенного числа Р(A), называемого математической вероятностью события А, и каков объективный смысл этой оценки. Ясное понимание взаимоотношения между философскими категориями случайного и необходимого является неизбежным предварительным условием успешного анализа понятия математической вероятности, но этот анализ не может быть полным без ответа на поставленный нами вопрос о том, при каких условиях случайность допускает количественную оценку в виде числа вероятности.

Число различных определений математической вероятности, предложенное теми или иными авторами, очень велико. Мы не станем сейчас разбираться во всех логических тонкостях этих многочисленных определений. Всякое научное определение такого рода основных понятий, как понятие вероятности, является лишь утонченной логической обработкой некоторого запаса очень простых наблюдений и оправдавших себя долгим успешным применением практических приемов. Интерес к логически безупречному «обоснованию» теории вероятностей возник исторически позднее, чем умение определять вероятности различных событий, производить вычисления с этими вероятностями, а также использовать результаты произведенных вычислений в практической деятельности и в научных исследованиях. Поэтому в основе большинства попыток научного определения общего понятия вероятности легко рассмотреть те или иные стороны конкретного познавательного процесса, приводящего в каждом отдельном случае к фактическому определению вероятности того или иного события, будь то вероятность выпадения хотя бы одной шестерки при четырех бросаниях игральной кости, или вероятность радиоактивного распада, или вероятность попадания в цель.

С очерченной сейчас точки зрения большинство определений математической вероятности может быть разделено на три группы:

• 1. Определения математической вероятности как количественной меры «степени уверенности» познающего субъекта — субъективная вероятность.
• 2. Определения, сводящие понятие вероятности к понятию «равновозможности» как к более примитивному понятию (так называемое «классическое» определение вероятности).
• 3. Определения, отправляющиеся от «частоты» появления события в большом количестве испытаний («статистическое» определение).

Указанные группы по отдельности обладают существенными недостатками и полное понимание природы вероятности требует их разумного синтеза.

Основные понятия теории вероятностей, определение и свойства вероятностей. Непосредственное вычисление вероятностей

Возникновение теории вероятностей

Возникновение теории вероятностей относится к середине XVII века, когда математики заинтересовались задачами, поставленными азартными игроками и до сих пор не изучавшимися в математике. В процессе решения этих задач выкристаллизовались такие понятия, как вероятность и математическое ожидание. При этом ученые того времени – Гюйгенс (1629-1695), Паскаль (1623-1662), Ферма (1601-1665) и Бернулли (1654-1705) были убеждены, что на базе массовых случайных событий могут возникать четкие закономерности. И только состояние естествознания привело к тому, что азартные игры еще долго продолжали оставаться тем почти единственным конкретным материалом, на базе которого создавались понятия и методы теории вероятностей. Это обстоятельство накладывало отпечаток и на формально-математический аппарат, посредством которого решались возникавшие в теории вероятностей задачи: он сводился исключительно к элементарно-арифметическим и комбинаторным методам.

Серьезные требования со стороны естествознания и общественной практики (теория ошибок наблюдения, задачи теории стрельбы, проблемы статистики, в первую очередь статистики народонаселения) привели к необходимости дальнейшего развития теории вероятностей и привлечения более развитого аналитического аппарата. Особенно значительную роль в развитии аналитических методов теории вероятностей сыграли Муавр (1667-1754), Лаплас (1749-1827), Гаусс (1777-1855), Пуассон (1781-1840). С формально-аналитической стороны к этому же направлению примыкает работа создателя неевклидовой геометрии Лобачевского (1792-1856), посвященная теории ошибок при измерениях на сфере и выполненная целью установления геометрической системы, господствующей во вселенной.

Теория вероятностей, подобно другим разделам математики, развилась из потребностей практики: в абстрактной форме она отражает закономерности, присущие случайным событиям массового характера. Эти закономерности играют исключительно важную роль в физике и других областях естествознания, разнообразнейших технических дисциплинах, экономике, социологии, биологии. В связи с широким развитием предприятий, производящих массовую продукцию, результаты теории вероятностей стали использоваться не только для браковки уже изготовленной продукции, но и для организации самого процесса производства (статистический контроль в производстве).

Основные понятия теории вероятностей

Теория вероятностей объясняет и исследует различные закономерности, которым подчинены случайные события и случайные величины. Событием является любой факт, который можно констатировать в результате наблюдения или опыта. Наблюдением или опытом называют реализацию определенных условий, в которых событие может состояться.

Опыт означает, что упомянутый комплекс обстоятельств создан сознательно. В ходе наблюдения сам наблюдающий комплекс этих условий не создает и не влияет на него. Его создают или силы природы или другие люди.

Что нужно знать, чтобы определять вероятности событий

Все события, за которыми люди наблюдают или сами создают их, делятся на:

• достоверные события;
• невозможные события;
• случайные события.

Достоверные события наступают всегда, когда создан определенный комплекс обстоятельств. Например, если работаем, то получаем за это вознаграждение, если сдали экзамены и выдержали конкурс, то достоверно можем рассчитывать на то, что включены в число студентов. Достоверные события можно наблюдать в физике и химии. В экономике достоверные события связаны с существующим общественным устройством и законодательством. Например, если мы вложили деньги в банк на депозит и выразили желание в определенный срок их получить, то деньги получим. На это можно рассчитывать как на достоверное событие.

Невозможные события определенно не наступают, если создался определенный комплекс условий. Например, вода не замерзает, если температура составляет плюс 15 градусов по Цельсию, производство не ведется без электроэнергии.

Случайные события при реализации определенного комплекса условий могут наступить и могут не наступить. Например, если мы один раз подбрасываем монету, герб может выпасть, а может не выпасть, по лотерейному билету можно выиграть, а можно не выиграть, произведенное изделие может быть годным, а может быть бракованным. Появление бракованного изделия является случайным событием, более редким, чем производство годных изделий.

Ожидаемая частота наступления случайных событий тесно связана с понятием вероятности. Закономерности наступления и ненаступления случайных событий исследует теория вероятностей.

Если комплекс нужных условий реализован лишь один раз, то получаем недостаточно информации о случайном событии, поскольку оно может наступить, а может не наступить. Если комплекс условий реализован много раз, то появляются известные закономерности. Например, никогда невозможно узнать, какой кофейный аппарат в магазине потребует очередной покупатель, но если известны марки наиболее востребованных в течение длительного времени кофейных аппаратов, то на основе этих данных возможно организовать производство или поставки, чтобы удовлетворить спрос.

Знание закономерностей, которым подчинены массовые случайные события, позволяет прогнозировать, когда эти события наступят. Например, как уже ранее отмечено, заранее нельзя предусмотреть результат бросания монеты, но если монета брошена много раз, то можно предусмотреть выпадение герба. Ошибка может быть небольшой.

Методы теории вероятностей широко используются в различных отраслях естествознания, теоретической физике, геодезии, астрономии, теории автоматизированного управления, теории наблюдения ошибок, и во многих других теоретических и практических науках. Теория вероятностей широко используется в планировании и организации производства, анализе качества продукции, анализе технологических процессов, страховании, статистике населения, биологии, баллистике и других отраслях.

Случайные события обычно обозначают большими буквами латинского алфавита A, B, C и т.д.

Случайные события могут быть:

События A, B, C … называют несовместными, если в результате одного испытания может наступить одно из этих событий, но невозможно наступление двух или более событий.

Если наступление одного случайного события не исключает наступление другого события, то такие события называют совместными. Например, если с ленты конвейера снимают очередную деталь и событие А означает «деталь соответствует стандарту», а событие B означает «деталь не соответствует стандарту», то A и B – несовместные события. Если событие C означает «взята деталь II сорта», то это событие совместно с событием A, но несовместно с событием B.

Если в каждом наблюдении (испытании) должно произойти одно и только одно из несовместных случайных событий, то эти события составляют полное множество (систему) событий.

Достоверным событием является наступление хотя бы одного события из полного множества событий.

Если события, образующие полное множество событий, попарно несовместны, то в результате наблюдения может наступить только одно из этих событий. Например, студент должен решить две задачи контрольной работы. Определенно произойдет одно и только одно из следующих событий:

• будет решена первая задача и не будет решена вторая задача;
• будет решена вторая задача и не будет решена первая задача;
• будут решены обе задачи;
• не будет решена ни одна из задач.

Эти события образуют полное множество несовместных событий.

Если полное множество событий состоит только из двух несовместных событий, то их называют взаимно противоположными или альтернативными событиями.

Событие, противоположное событию , обозначают . Например, в случае одного подбрасывания монеты может выпасть номинал () или герб ().

События называют равновозможными, если ни у одного из них нет объективных преимуществ. Такие события также составляют полное множество событий. Это значит, что в результате наблюдения или испытания определенно должно наступить по меньшей мере одно из равновозможных событий.

Например, полную группу событий образуют выпадение номинала и герба при одном подбрасывании монеты, наличие на одной печатной странице текста 0, 1, 2, 3 и более 3 ошибок.

Определения и свойства вероятностей

Классическое определение вероятности. Возможностью или благоприятным случаем называют случай, когда при реализации определённого комплекса обстоятельств события А происходят. Классическое определение вероятности предполагает напрямую вычислить число благоприятных случаев или возможностей.

Классическая и статистическая вероятности. Формулы вероятностей: классической и статистической

Вероятностью события А называют отношение числа благоприятных этому событию возможностей к числу всех равновозможных несовместных событий N, которые могут произойти в результате одного испытания или наблюдения. Формула вероятности события А:

(1)

Если совершенно понятно, о вероятности какого события идёт речь, то тогда вероятность обозначают маленькой буквой p, не указывая обозначения события.

Чтобы вычислить вероятность по классическому определению, необходимо найти число всех равновозможных несовместных событий и определить, сколько из них благоприятны определению события А.

Пример 1. Найти вероятность выпадения числа 5 в результате бросания игральной кости.

Решение. Известно, что у всех шести граней одинаковая возможность оказаться наверху. Число 5 отмечено только на одной грани. Число всех равновозможных несовместных событий насчитывается 6, из них только одна благоприятная возможность выпадения числа 5 (М = 1). Это означает, что искомая вероятность выпадения числа 5

Пример 2. В ящике находятся 3 красных и 12 белых одинаковых по размеру мячиков. Не глядя взят один мячик. Найти вероятность, что взят красный мячик.

Решение. Искомая вероятность

Найти вероятности самостоятельно, а затем посмотреть решение

Пример 3. Бросается игральная кость. Событие B — выпадение чётного числа. Вычислить вероятность этого события.

Пример 4. Бросается игральная кость. Какова вероятность выпадения числа 7?

Пример 5. В урне 5 белых и 7 чёрных шаров. Случайно вытаскивается 1 шар. Событие A — вытянут белый шар. Событие B — вытянут чёрный шар. Вычислить вероятности этих событий.

Классическую вероятность называют также априорной вероятностью, так как её рассчитывают перед началом испытания или наблюдения. Из априорного характера классической вероятности вытекает её главный недостаток: только в редких случаях уже перед началом наблюдения можно вычислить все равновозможные несовместные события и в том числе благоприятные события. Такие возможности обычно возникают в ситуациях, родственных играм.

Сочетания. Если последовательность событий не важна, число возможных событий вычисляют как число сочетаний:

(2)

Пример 6. В группе 30 студентов. Трём студентам следует направиться на кафедру информатики, чтобы взять и принести компьютер и проектор. Вычислить вероятность того, что это сделают три определённых студента.

Решение. Число возможных событий рассчитываем, используя формулу (2):

Вероятность того, что на кафедру отправятся три определённых студента:

Пример 7. Продаются 10 мобильных телефонов. Их них у 3 есть дефекты. Покупатель выбрал 2 телефона. Вычислить вероятность того, что оба выбранных телефона будут с дефектами.

Решение. Число всех равновозможных событий находим по формуле (2):

По той же формуле находим число благоприятных событию возможностей:

Искомая вероятность того, что оба выбранных телефона будут с дефектами:

Найти вероятность самостоятельно, а затем посмотреть решение

Пример 8. В экзаменационных билетах 40 вопросов, которые не повторяются. Студент подготовил ответы на 30 из них. В каждом билете 2 вопроса. Какова вероятность того, что студент знает ответы на оба вопроса в билете?

Свойства вероятностей

Свойство 1. Если можно вычислить возможности возникновения события А и их число совпадает общим числом равновозможных событий, то вероятность события А равна 1.

Например, при бросании игральной кости число возможностей выпадения чисел 1, 2, 3, 4, 5, 6 равно 6. Насчитывается также 6 равновозможных несовместимых событий. Таким образом, M = N и

Свойство 2. Вероятность невозможного события равна 0. Если число возможностей события А равна 0, то и

Например, при бросании игральной кости не может выпасть число 9, потому что такого числа нет на гранях игральной кости.

Свойство 3. Вероятность случайного события всегда больше 0 и меньше 1:

Определение статистической вероятности. В определении статистической вероятности используется понятие относительно частоты события А. Относительной частотой события А называют отношение числа наблюдений, в которых наблюдается А, к числу всех наблюдений. Относительную частоту обычно обозначают буквой W. Если в n наблюдениях событие А наблюдается m раз, то относительная частота события А:

Например, баскетболист у штрафной линии готовится совершить бросок. Из собранной тренером статистической информации известно, что у этого баскетболиста из 100 штрафных бросков успешны 70. Вероятность того, что баскетболист реализует штрафной бросок:

Длительные наблюдения показали, что с увеличением числа наблюдений относительная частота события А становится всё более стабильной. Число, около которого при серии наблюдений колеблется относительная частота, называется статистической вероятностью события А. Формула статистической вероятности события А:

если .

Вычислить точную статистическую вероятность невозможно, так как невозможно выбрать бесконечно большое число наблюдений.

Преимущество статистического определения вероятности в том, что оно не требует априорных знаний об исследуемом объекте. Классическую вероятность можно вычислить до наблюдения или испытания, а статистическую – после наблюдения или испытания.