Существуют два подхода к определению натуральных чисел — это числа, возникающие при:
подсчёте (нумерации) предметов (первый, второй, третий, …);
обозначении количества предметов (нет предметов, один предмет, два предмета, …).
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли ноль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход [1]. Второй подход, например, применяется в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств. Кроме того, отсчёт с нуля широко распространён в программировании (например, для индексации массивов, нумерации битов машинного слова и т. д.).
Отрицательные и нецелые (рациональные, вещественные, …) числа к натуральным не относятся.
Множество всех натуральных чисел принято обозначать символом > \mathbb
Все конечные множества можно распределить по классам в зависимости от количества в них элементов, т.е. в каждом классе будут находиться равномощные множества. Они различны по своей природе, но содержат поровну элементов.
С теоретико-множественной позиции количественное натуральное число есть общее свойство класса конечных равномощных множеств.
Каждому классу соответствует только одно натуральное число, каждому натуральному числу – только один класс равномощных множеств.
Рассмотрим, например множества:
— множество букв в слове «число»;
— множество сторон в пятиугольнике.
В этих множествах одинаковое число элементов, в чем можно убедиться, установив взаимно однозначные соответствия между ними. Это общее, что характеризует каждое из множеств одного класса, называется натуральным числом. Данные множества характеризуются числом пять. Это число характеризует свойство и других множеств этого класса.
Каждому конечному множеству соответствует только одно натуральное число, но каждому натуральному числу соответствуют различные равномощные множества из одного класса.
1) «Сколько пальцев на руке?»
2) «Возьми пять любых предметов».
В первом случае ответ однозначный (пять), во втором возможны различные варианты выполнения задания.
Число «нуль» не является натуральным.
С точки зрения теории множеств число «нуль» рассматривается как число элементов пустого множества.
Знакомя дошкольников с различными числами и их записью с помощью цифр, показывают различные равномощные множества и соотносят им изучаемое число:
— На рисунке изображены три фигуры.
— На столе лежат три яблока.
— Маша, Коля, Вася — это три имени.
— Число «три» записывают цифрой 3, что обозначает «три предмета».
Так как натуральное число оказывается связанным с конечным множеством, то и действия над натуральными числами можно рассматривать в связи с действиями над множествами. Так, сложение чисел связывают с объединением непересекающихся множеств, а вычитание — с дополнением подмножества.
Пусть а – число элементов в множестве А, b – число элементов в множестве В, и множества А и В не пересекаются. Тогда суммой натуральных чисел аиbназывают число элементов в объединении множеств А и В.
Сумма натуральных чисел всегда существует, единственно и но зависит от выбора представляющих их множеств.
Рассмотрим пример. Пусть 2 – число элементов в множестве А (А может быть множеством из двух яблок, множеством из двух геометрических фигур и т. д.), 3 – число элементов в множестве В (В – может быть множеством из трех треугольников, множеством из трех груш и т.д.). Множества А и В не должны иметь общих элементов. Тогда 2 + 3 представляет собой число элементов в объединении множеств А и В. Если пересчитать их, то получим, что 2 + 3 = 5.
Действие, при помощи которого находят сумму, называют сложением, а числа, которые складывают, слагаемыми.
Исходя из данного определения суммы, можно обосновать известные законы сложения чисел:
1) переместительный, т.е. а + b = b + а для любых натуральных, чисел аиb.
2) сочетательный, т.е. (а + b) + с = а + (b + с) для любых натуральных чисел а , b и с.
Переместительный и сочетательный законы сложения распространяются на сложение любого числа слагаемых. Переместительный закон разрешает любую перестановку слагаемых, а сочетательный – любую их группировку.
Дошкольники используют эти законы при поиске удобного способа нахождения суммы. Так, считается более простым прибавлять меньшее слагаемое к большему, удобнее складывать слагаемые, дополняющие друг друга до 10 и т.п.
Задание 26.
Если 0 – число элементов пустого множества, то каков смысл суммы а + 0 ?
Сравнение чисел также можно выполнять, оперируя с множествами. Например, чтобы установить отношение 3 а). Если множества А и В равномощны, то а = b.
Можно определить отношение «меньше» для чисел, не обращаясь к множествам. Например, было 5 яблок, добавили 1, стало 6 яблок. Яблок стало больше на 1, значит 6 больше 5, а 5 меньше 6.
Число а меньше числа b тогда и только тогда, когда существует такое натуральное число с , что а + с = b.
Как уже было сказано, вычитание чисел связано с дополнением подмножества.
Пусть а – число элементов в множестве A, b – число элементов в множестве В и В – подмножество множества А. Тогда разностью натуральных чисел а и b называется число элементов в дополнении множества В до множества А.
Действие, при помощи которого находят разность а — b, называется вычитанием, число а — уменьшаемым, число b — вычитаемым.
Например, смысл разности 5-3 можно объяснить следующим образом. Возьмем множество А, в котором 5 элементов (квадратов, яблок и др.).Выделим из множества А подмножество В, в котором 3 элемента. Тогда 5-3 будет представлять число элементов в дополнении множества В до множества А. Путем пересчета можно установить, что 5-3 = 2.
Разность натуральных чисел а и b существует и единственна только при условии, что b
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9116 — 

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
ТЕОРЕТИКО-МНОЖЕСТВЕННЫЙ СМЫСЛ НАТУРАЛЬНОГО ЧИСЛА, НУЛЯ
Количественное натуральное число: С теоретико-множественной точки зрения количественное натуральное число — это общее свойство класса непустых конечных равномощных друг другу множеств.
Ноль — это количественная характеристика пустого множества, 0=n
Отрезок натурального ряда. Пусть а — натуральное число, тогда множество всех натуральных чисел, не превосходящих числа а, называют отрезком натурального ряда и обозначают Na.
Пересчитать элементы конечного множества X — это значит установить взаимно однозначное соответствие между множеством X и отрезком натурального ряда Na , число а будет называться числом элементов в множестве X и обозначаться n(X) = а
начинать пересчет можно с любого элемента множества,
ни один элемент не должен быть пропущен,
каждый элемент считают только один раз.
Количественное натуральное число отвечает на вопрос «сколько элементов в множестве?» и выражается числительными «один», «два», «три», и т.д.
Порядковое натуральное число отвечает на вопрос «которым по счету является данный элемент в множестве?» и выражается числительными «первый», «второй», «третий» и т.д.
Равные натуральные числа. Натуральные числа а и b называются равными, если они являются характеристиками равномощных множеств. a=b n(A)=n(B), n(A)=a, n(B)=b, A B.
Свойства отношения равенства на N.
- 1) рефлексивность (aN), a=a
- 2) симметричность (a,bN), если a=b, тоb=a
- 3) транзитивность а,b,cN), если а=b, b=с, то а=с
Отношение «меньше» на N
1 подход Пусть а и b — натуральные числа, а
Натуральное число с точки зрения количественной теории это
Комплекс упражнений Бейтса для восстановления зрения
Для лечения суставов наши читатели успешно используют Око-плюс. Видя, такую популярность этого средства мы решили предложить его и вашему вниманию.
Подробнее здесь…
Сколько в мире людей, носящих очки? И с каждым днем зрение только ухудшается. Большинство из них думают, что кроме проведения операции на глаза, им ничего не поможет. Как же они ошибаются!
На рубеже веков американский врач-офтальмолог разработал систему упражнений, которые помогут вылечить близорукость, дальнозоркость и даже астигматизм. Эта революционная система за время своего существования помогла не одной тысяче людей избавиться от очков и линз и наслаждаться окружающим миров. Звали этого человека Уильям Бейтс.
Выбор упражнений огромен. Если выполнять хотя бы 15 из них ежедневно без пропусков, то уже спустя пару недель можно заметить снятие усталости с глаз и постепенное улучшение зрения. На каждого человека система действует по-разному. Но замечено, что за год большинству людей удается окончательно распрощаться с очками. В дальнейшем необходимо лишь проводить периодически недельные курсы раз в месяц для профилактики.
Зачем лишать себя удовольствия видеть мир четко и без размытых контуров, если за короткое время можно привести зрение в порядок?
Кто такой Уильям Бейтс?
Бейтc родился в далеком 1860 году и посвятил свою жизнь офтальмологии. Богатый практический опыт, наблюдения за пациентами и исследования позволили врачу разработать собственную систему упражнений, который улучшают зрение.
В 1917 году он открыл первые курсы занятий для желающих хорошо видеть. Три года спустя он выпустил книгу-сборник упражнений. Постепенно направление завоевывало популярность и даже получило название «бейтсизм».
После смерти доктора в 1931 году его дело перешло к его жене, которая продолжила его. Все быстрее росло число последователей предложенного Бейтсом способа лечения. До сих пор оно не теряет своей актуальности. Наиболее известными пропагандистами метода в России являются В. Жданов и Г. Шичко, которые доработали систему Бейтса и внедряют ее дальше, даря людям возможность вылечить глазные недуги.
Основа теории «бейтсизма»
В основу упражнений легло утверждение, что зрение в немалой степени зависит от тонуса глазных мышц. И психическое напряжение в немалой степени влияет на них. А значит для того, чтобы улучшить зрение, их надо расслабить. За счет этого нормализуется кровообращение в глазном яблоке и прилежащей области, что, несомненно, ведет к улучшению зрения. 6 мышц отвечают за зрение. И гимнастика для глаз направлена на то, чтобы они отдыхали и восстанавливались. Например, при взгляде влево, отдыхают правые мышцы. Если человек смотрит наверх, то нижние глазодвигательные мышцы в этот момент расслаблены.
Позже коллеги-офтальмологи эти утверждения доктора опровергли и научно доказали, что качество видения зависит вовсе не от этого. Тем не менее, многочисленные поклонники метода доказали, что он работает. Они смогли наконец-то начать нормально ориентироваться в пространстве без очков!
Основные положения
Доктор Бейтс настоятельно советовал своим ученикам отложить очки в дальний угол и попробовать жить без них. По его словам они приносят только вред. Да, они позволяют лучше видеть предметы и избавиться от расплывчатых очертаний. Но при этом они наносят несравненный вред глазам. Эти его слова полностью идут в разрез со словами других врачей и медицины. Как только у человека портится зрение, ему немедленно прописывают ношение очков. Действительно ли это забота о его глазах или же продуманный ход огромных медицинских корпорации, которые зарабатывают огромные суммы денег на продаже очков.
Кто постоянно носит очки, наверное, не раз замечали за собой, как тяжело перефокусироваться, когда резко их снимаешь. И как сильно напряжены глаза в эти моменты. Можно даже ощущать боль. Это идет смена напряжения мышц. И лишь через минут 10-15 ощущения нормализуются. Тем, кто рискнул несколько дней продержаться без очков, замечают, что зрение становится острее. Поэтому во время гимнастики рекомендуется полностью избавиться от очков и линз, за исключением редких случаев, когда без них никак не обойтись.
Второй постулат гласит о том, что чтение при плохом освещении ухудшает зрение. Эту истину еще с детства многие родители вдалбливают в голову своим детишкам. Бейтс же рекомендует постоянно менять степень освещения. То яркое, то тусклое. Это заставит поработать глаза и нормализует кровообращение в них.
Третье опровержение доктора состоит в том, что читать в едущем транспорте не просто можно, а необходимо. Да, строки трясутся и разбегаются. Но это заставляет работать глаза более усиленно, и способствует улучшению зрения.
Видео — Комплекс упражнений для улучшения зрения по Бейтсу
Почему так много противников «бейтсизма»
С самого начала появления комплекса упражнений У. Бейтса у него нашлись противники. Еще при жизни доктора академия офтальмологии выдвинула обвинение, что доктор обманщик и лишь завлекает людей ради прибыли от курсов. Несколько врачей-офтальмологов выступали с заявлениями, что исследования показывают, что система не работает. Среди них был и довольно известный профессор М.Мохан. Критики этого метода лечения появляются постоянно.
Странно, если учитывать, сколько людей по всему миру удалось благодаря этой гимнастике восстановить зрение. Так почему же метод не стал повсеместной панацеей от слеповатости, а клиники по лазерной коррекции зрения растут как на дрожжах?
Во-первых, медицина приносит огромные деньги. А Бейтс в наглую лишает многих компаний прибыли от продажи линз и очков. Сколько лекарственных препаратов продается ежедневно тем, у кого плохое зрение. Счет идет на миллиарды. Так неужели компании позволят лишать себя таких денег потому, что некий доктор нашел эффективный, простой и, главное, бесплатный способ улучшения зрения? Нет конечно. Они потеряют огромные суммы, если люди перестанут покупать различные таблетки и БАДы, приобретать новые очки и ежемесячно менять свои линзы. С утверждениями доктора будут бороться. Будут открываться новые факты, почему нельзя следовать «бейтсизму». Авторитетные врачи будут заявлять, что система не работает.
Несмотря на желание медицинских корпораций похоронить этот метод лечения, многие сторонники доктора Бейтса борются и на собственном примере доказывают, что его гимнастика для глаз действительно работает. Почему бы не попробовать и вам? Вы ничего не теряете, зато можете многое приобрести.
Вторая причина – лень большинства людей. Не у каждого хватает силы воли выполнять ежедневно комплекс упражнений. Первые недели они занимаются усердно и с удовольствием. Постепенно запал сгорает, и находятся причины начать пропускать занятия. Один день не сделали, другой, и вот уже полностью пропадает желание делать гимнастику. Пару дней занятий ничего не дадут. Необходимы месяцы для получения сколь-нибудь существенного результата. Лишь через год-полтора зрение полностью восстановится. Не у всех хватает терпения заниматься так долго. Лишь 10 процентов желающих проходят до конца и излечиваются от недуга. Остальным проще носить очки, тратить бешеные деньги на медпрепараты, обещающие выздоровление и раздумывать над лазерной коррекцией зрения. И так из года в год. А зрение падает. Очки заменяются на более сильные. И ситуация повторяется.
Если же уже решили заняться своим зрением и восстановить его, то стоит идти до конца. Собрать волю в кулак и заниматься ежедневно. Упражнения простые. 15-20 минут на них можно выделить всегда. При любых обстоятельствах.
Основные типы упражнений
Все виды упражнений, предлагаемых Уильямом Бейтсом можно разделить на несколько категорий:
Под этим любопытным словом скрывается всего-навсего отдых для глаз. А название произошло от того, что руками закрываются глаза, чтобы избежать даже малейшего проникновения света. Необходимо сесть, закрыть глаза и расслабиться. Главная цель – по максимуму расслабить глазные мышцы. Зачастую бывает, что как только человек закрыл глаза, ему начинают чудиться различные блики, играющие цветовые пятна, возникают искры. Показателем, что наступило максимальное расслабление и все делается верно, является абсолютная чернота перед глазами. Ничего больше.
Необходимо попробовать визуализировать что-то, попытать думать о приятном. Постепенно, если получается возникать образы, переходить на воображение черных предметов, пока все пространство не станет абсолютно черным и не исчезнут светлые пятна.
Это упражнение является ключевым и с него начинается весь комплекс. Рекомендуется его делать 3-4 раза и лишь затем переходить к остальным.
Помощником для этого занятия является солнце. Необходимо смотреть на него в течение нескольких секунд ежедневно. Суть упражнения состоит в приучении своих глаз к яркому свету.
Необходимо попробовать восстановить в памяти какие-либо события или ощущения из прошлого. Когда человек вспоминает что-то приятное, он расслабляется. Его психика становится не такой натянутой, все мышцы тела, в том числе и глаз, находятся в состоянии покоя.
Необходимо закрыть глаза и попытаться себе что-то представить. Не надо пытаться увидеть каждую мелочь. Образ должен быть общим и резко сменяться. Можно перебирать в уме какие-либо предметы или, например, буквы. Бейтс полагал, что зрение и зрительная память тесно связаны. И для нормализации остроты видения необходимо навести порядок с представлением вещей.
При перемещении зрачка в какую-либо сторону напрягается один вид глазных мышц, а другие в это время расслабляются. На этом и основываются упражнения на перемещение. Требуется смотреть то в одну сторону, то в другую и постоянно чередовать.
Наблюдение за раскачивающимся предметом приводит к частой смене мышц и движению глазного яблока. А что может быть лучшей зарядкой?
Быстрое открытие и закрытие глаз с попыткой фокусирования за этот короткий промежуток времени также может принести немалую пользу здоровью глаз.
Всего Уильям Бейтс предложил более 100 упражнений, которые можно выделить в вышеперечисленные группы. Рекомендуется выполнять не менее 15 из них и ежедневно. Через некоторое время упражнения можно менять. Но ни в коем случае нельзя прекращать занятия. Все это сведет на нет усилия, и приведет к напрасной трате времени.
Упражнения
1.Следует на расстоянии посмотреть на какую-нибудь букву крупной надписи. После этого необходимо сесть, расслабиться и закрыть глаза руками. Попробуйте вспомнить букву и ее оттенок. В мыслях немного видоизмените ее цвет на более черный. Откройте глаза и посмотрите опять на эту букву. Она покажется чернее. Повторить несколько раз это упражнение. Вы достигнете того, что эта буква будет ярче выделяться черным и вы ее быстрее будете выхватывать из изображения. Вы начнете лучше ее видеть.
2. Перед закрытыми глазами представьте по очередности все цвета в порядке от более светлого к темному. Не стоит пытаться удержать оттенок долго. Секунды достаточно. Цвета должны мелькать и быстро сменяться. Пару минут для этого упражнения будет достаточно.
Затем попробуйте представить кусочек белого мела на черном фоне. Резкий контраст сделает, что чернее этого фона уже будет сложно что-либо представить.
Воспоминание
1.Вызовите в своих воспоминаниях розу. Но не стоит пытаться ее детализировать. Вместо этого лучше попытайтесь представить некий предмет на ней. Например, муравья или какого-нибудь жучка. Вот он ползет по стеблю, быстро перебирается на лист, возвращается обратно. Теперь он уже на бутоне. И в подобном духе.
Вы заметите, что во время процесса, хоть вы и пытались представить один предмет, тем не менее особого напряжения вы не испытывали. Движущийся объект немного отвлекал и рассеивал внимание, делая воспоминание легким.
2. Повесьте на приличном расстоянии, 3-6 метров таблицу Сивцева с буквенными обозначениями. Посмотрите на какую-либо букву и пытайтесь ее представить. При этом в воображение черную часть делайте еще чернее, а светлую – белее. В этом случае представление накладывается на воспоминание. Откройте глаза и посмотрите на эту букву. После пару раз повторений вы сможете эту букву видеть четче. Постепенно можно пытаться представить уже целую строку, а может даже и две.
Соляризация
1.Закройте глаза и обратитесь лицом к солнцу. Медленно вращайте голову в разные стороны. Продолжайте минут 5. Откройте на краткое мгновение глаза, продолжая вращать голову. Не пытайтесь смотреть на солнце, лучше на область рядом с ним. По мере привыкания можно кидать взгляд ближе к солнцу.
2. Сядьте лицом к солнцу. Расслабьтесь как можно больше. Прикройте глаза и смотрите в сторону солнца. Плавно поворачивайте голову из стороны в сторону. Ни в коем случае не стоит полностью открывать глаза. Продолжать пару минут.
Перемещение и раскачивание
1.Двигая голову влево-вправо, обращайте в ту же сторону взгляды. Чуть позже без шевеления головы попытайтесь смотреть в разные стороны. Вы должны почувствовать напряжение в глазных мышцах
2.Закройте глаза и раскачивайте голову словно маятник. Вы удивитесь, но ваши глазные яблоки будут также двигаться в такт головы.
Для лечения суставов наши читатели успешно используют Око-плюс. Видя, такую популярность этого средства мы решили предложить его и вашему вниманию.
Подробнее здесь…
3.Шагайте с раскачиванием тела. Один шаг и качните головой, глаза должны следовать тому же движению. Затем следующий шаг. И так раз 15-20.
4. Держите книгу перед глазами и двигайте ее. Следите зрением за ее движением.
Моргание и проблески
1.Упражнение следует выполнять перед зеркалом. Смотрите на правый глаз. Моргните. Повторите для другого. Раз 15 будет на каждый глаз будет достаточно.
2. На расстоянии в 2 метр повесьте проверочную таблицу с буквами и постарайтесь рассмотреть самые мелкие строчки. Разглядывайте их минут 5-7. Главное условие упражнения – моргать после чтения каждой буквы.
3. При ходьбе постарайтесь моргать каждый раз, как только ваша ступня коснутся земли. Упражнение рекомендуется делать не менее 10 минут.
4. Можно устроить неплохое занятие с мячом. Необходимо быстро-быстро перекидывать его из руки в руку и при этом моргать, как только мяч куда-нибудь летит.
5. Возьмите в руки книгу, напечатанную мелким шрифтом. Смотрите только на белые промежутки между строками. На каждой светлой полосе моргайте. В скором времени вы заметите, что слова становятся четче и уже не так сливаются. Это упражнение является прекрасной профилактикой от быстрой усталости глаз.
Такая гимнастика для глаз очень простая и занимает минимум времени. Если хотите быстрее достигнуть результата, делайте по несколько раз на день. Даже если у вас неплохое зрение, но вы стали замечать, что глаза быстро устают, то делайте пару упражнений для профилактики. И вы заметите, как глаза расслабляются, уходит напряжение и вы начинаете чувствовать себя лучше.
Для людей с серьезными заболеваниями глаз метод доктора Бейтса стал панацеей от проблем. Он помогает полностью восстановить зрение и избавиться от ежедневного ношения очков. Вы наконец-то почувствуете вкус к жизни.
Но стоит помнить, что как и любая гимнастика, этот комплекс упражнений требует времени и силы воли. Не стоит его закидывать спустя пару недель, даже если вы и почувствовали улучшение и решили, что вам этого достаточно. Вы можете восстановить зрение до максимальной частоты! Опыт тысячи людей, опробовавших на себе эту зарядку для глаз может подтвердить эффективность метода. А его простота удивляет!
Определение натурального числа и число 0 в количественной теории.
Дата добавления: 2014-05-19 ; просмотров: 934 ; Нарушение авторских прав
Два конечных мн.А и В называются равномощными, если между ними можно установить взаимно однозначное соответствие. Отношение «мн.А равномощно мн.В» рефлексивно (А
А), симметрично (А
А) и транзитивно (А
С). Значит, оно яв-ся отношением эквивалентности, а потому позволяет разбить совокупность всех мн.на классы эквивалентности так, что любые два мн.одного класса эквивалентны, а любые два мн.разных классов не эквивалентны. В одном классе могут содержаться разные мн., но общим у них яв-ся то, что все они имеют одинаковое кол-во элементов. П: рассмотрим мн.: вершины треугольника, буквы слова «дом», цифры числа 123. Между элементами этих мн.можно установить взаимно однозначное соответствие. Значит, они равномощные. Натуральное число есть общее св-во класса конечных равномощных множеств. Каждому классу соответствует одно и только одно нат.число, а каждому числу- один и только один класс конечных равномощных мн. Каждому мн.соответствует только одно нат.число: а=п(А), но каждому числу а соответствуют разные мн.одного и того же класса эквивалентности. П: число 4 есть общее св-во класса мн.: времена года, стороны света, стихии, буквы слова «парк», вершины квадрата. Число 0 ставится в соответствие пустому мн.: 0=п(∅). Например, мн.корней уравнения х2+4=0 можно поставить в соответствие число 0, т.к.это уравнение корней не имеет. Мн.нат.чисел и число 0 образуют мн.целых неотрицательных чисел: N0=N∪.
1. Теоретико-множественный смысл натурального числа, нуля и отношения «меньше»
Как было установлено ранее, количественное натуральное число а получается в результате счета элементов конечного множества А: а = n(А). Это же число а может быть получено и при пересчете элементов другого множества, например, В. Но если а = n(В), то множества А и В равномощны, поскольку содержат поровну элементов.
Так как любому непустому конечному множеству соответствует только одно натуральное число, то вся совокупность конечных множеств разбивается на классы равномощных множеств. В одном классе будут содержаться все одноэлементные множества, в другом — двухэлементные и т.д. Множества одного класса различны по своей природе, но все они содержат одинаковое число элементов. И это число можно рассматривать как общее свойство класса конечных равномощных множеств.
Таким образом, с теоретико-множественной точки зрения, натуральное число — это общее свойство класса конечных равномощных множеств.
Так как каждый класс равномощных конечных множеств однозначно определяется выбором какого-нибудь его представителя, то о натуральном числе «три» можно сказать, что это общее свойство класса множеств, равномощных, например, множеству сторон треугольника, а о натуральном числе «четыре», что это общее свойство класса множеств, равномощных, например, множеству вершин квадрата.
Число «нуль» с теоретико-множественных позиций рассматривается как число элементов пустого множества: 0 = n().
Итак, натуральное число а как характеристику количества можно рассматривать с двух позиций:
1) как число элементов в множестве А, получаемое при счете, т.е. а = n(А), причем А Nа;
2) как общее свойство класса конечных равномощных множеств. Установленная связь между конечными множествами и натуральными числами позволяет дать теоретико-множественное истолкование отношения «меньше».
Натуральное число с точки зрения количественной теории это
Натуральные числа имеют две основные функции:
— характеристика количества предметов;
— характеристика порядка предметов, размещенных в ряд.
В соответствии с этими функциями возникли понятия порядкового числа (первый, второй и т.д.) и количественного числа (один, два и т.д.).
Долго и трудно человечество добиралось до 1-го уровня обобщения чисел. Сто веков понадобилось, чтобы выстроить ряд самых коротких натуральных чисел от единицы до бесконечности: 1, 2, … ?. Натуральных потому, что ими обозначались (моделировались) реальные неделимые объекты: люди, животные, вещи…
Аксиоматическая теория описывает натуральное число как элемент бесконечного ряда, в котором числа располагаются в определенном порядке, существует первое число и т.д. Иными словами, в аксиоматике раскрывается порядковый смысл натурального числа. Но натуральные числа имеют и количественный смысл. Чтобы выяснить, как связаны между собой эти два смысла натурального числа, рассмотрим такие понятия, как отрезок натурального ряда, конечное множество, счет и другие.
Отрезком Na натурального ряда называется множество натуральных чисел, не превосходящих натурального числа а.
Отрезок натурального ряда имеет два важных свойства:
1) любой отрезок Na содержит единицу. Это свойство вытекает из определения отрезка Na.
2) если число х содержится в отрезке Na и х ? а, то и непосредственно следующее за ним число х+1 также содержится в Na.
Множество А называется конечным, если оно равномощно некоторому отрезку Na натурального ряда.
Теорема: всякое непустое конечное множество равномощно одному и только одному отрезку натурального ряда.
Если непустое конечное множество А равномощно отрезку Na, то натуральное число а называют числом элементов множества А и пишут n(A)=a.
Установление взаимно однозначного соответствия между элементами непустого множества А и отрезком натурального ряда называется счетом элементов множества А.
Таким образом, всякое натуральное число а можно рассматривать как характеристику численности некоторого конечного множества А. Натуральное число а имеет при этом количественный смысл. Стойлова Л.П. Математика: Учебник для студентов отделений и факультетов начальных классов средний и высших педагогических учебных заведений. — М.: Академия, 1997. — С. 282-283.
Теоретико-множественный смысл натурального числа, нуля
Так как любому непустому конечному множеству соответствует только одно натуральное число, то вся совокупность конечных множеств разбивается на классы равномощных множеств. В одном классе будут содержаться все одноэлементные множества, в другом двухэлементные и т.д. Множества одного класса различны по своей природе, но все они содержат одинаковое число элементов. И это число можно рассматривать как общее свойство класса конечных равномощных множеств.
Таким образом, с теоретико-множественной точки зрения, натуральное число — это общее свойство класса конечных равномощных множеств.
Число «нуль» с теоретико-множественных позиций рассматривается как число элементов пустого множества: 0=n(Ш).
Итак, натуральное число а как характеристику количества можно рассматривать с двух позиций:
1) как число элементов в множестве А, получаемое при счете, т.е. а=n(А), причем А
2) Как общее свойство класса конечных равномощных множеств.
Теорема: Любое непустое подмножество конечного множества конечно. Там же. — С. 284-286.
Смысл натурального числа, полученного в результате измерения величины
Выясняя смысл натурального числа как меры величины, все рассуждения будем вести на примере одной величины — длины отрезка.
Уточним сначала понятие «отрезок состоит из отрезков».
Определение. Считают, что отрезок x состоит из отрезков x1, x2, …, xn, если он является их объединением и никакие два из них не имеют общих внутренних точек, хотя и могут иметь общие концы.
Пусть задан отрезок х, его длину обозначим Х. выберем из множества отрезков некоторый отрезок е, назовем его единичным отрезком, а длину обозначим буквой Е.
Определение: Если отрезок х состоит из отрезков, каждый из которых равен единичному отрезку е, то число а называют численным значением длины Х данного отрезка при единице длины Е.
Из данного определения получаем, что натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется. При выбранной единице длины Е это число единственное.
В связи с таким подходом к натуральному числу отметим два замечания:
1) при переходе к другой единице длины численное значение длины заданного отрезка изменяется, хотя сам отрезок остается неизменным.
2) если отрезок х состоит из а отрезков, равных е, а отрезок у — из b отрезков, тогда а = b тогда и только тогда, когда отрезки х и у равны. Стойлова Л.П. Математика: Учебник для студентов отделений и факультетов начальных классов средний и высших педагогических учебных заведений. — М.: Академия, 1997. — С. 309-311.
Основные идеи количественной теории натуральных чисел
В количественной теории натуральное число с самого начала воспринимается как число элементов (мощность, численность) конечного множества.
Что такое конечное множество? Для разъяснения одного из возможных определений воспользуемся интуитивными представлениями бесконечного и конечного множества, в частности о натуральном ряде 1, 2, 3, . в качестве образца бесконечного множества и его правильной части (подмножества) четных чисел 2, 4, 6, . .
Вопрос «Каких чисел больше: всех натуральных или всех четных?» кажется тривиальным, а правильный ответ парадоксальным.
Действительно, можно установить взаимно однозначное соответствие между элементами этих двух множеств:
1, 2, 3. к.
откуда интуитивно ясно, что четных чисел ровно столько, сколько и всех натуральных чисел.
Парадоксальность этого результата связана с тем, что такое соответствие возможно лишь в случае бесконечного множества.
Если же взять какое-нибудь конечное множество, то не удастся установить взаимно однозначное соответствие между всем множеством и какой-нибудь его (правильной, т. е. не совпадающей со всем множеством) частью.
Это, как правило, является определяющей характеристикой конечного множества.
Таким образом можно определить конечное множество: множество А называется конечным, если нельзя установить взаимно однозначное соответствие между всем этим множеством и какой-нибудь его правильной частью.
Рассмотрим теперь всевозможные конечные множества (говорят «класс или семейство множеств») и установим для них отношение эквивалентности следующим образом: два множества А и В будем называть эквивалентными (обозначается это через А
В), если между элементами этих множеств можно установить взаимно однозначное соответствие.
Установленное таким образом отношение множеств является отношением типа эквивалентности, т. е. рефлексивно, симметрично и транзитивно: для любых множеств Л, В, С:
Поэтому введенное отношение порождает разбиение данного семейства множеств на классы эквивалентности так, что любые два множества одного класса эквивалентны, а любые два множества различных классов неэквивалентны.
Эквивалентные множества не совпадают полностью, всеми своими свойствами: множество пальцев человеческой руки и множество, состоящее из пяти столов, различные, но эквивалентные множества.
Каждый класс эквивалентности характеризуется мощностью, т. е. любые два множества одного класса равномощны (имеют одинаковую мощность). Так как мы имеем дело лишь с конечными множествами, то равномощность означает равночисленность. Мощность или класс равночисленных конечных множеств и называют натуральным числом.
Таким образом, каждому конечному множеству А приписывают в качестве характеристики натуральное число m (Л), определяющее его принадлежность определенному классу эквивалентности. При этом множествам, принадлежащим одному классу эквивалентности, приписывается одно и то же натуральное число:
множествам, принадлежащим различным классам эквивалентности,— различные натуральные числа:
Так как А и В — конечные множества, то натуральные числа m (Л) и т (В) обозначают числа элементов (численность) этих множеств.
В основе такой концепции натурального числа лежит абстракция отождествления: отношение эквивалентности множеств отождествляет множества, принадлежащие одному классу эквивалентности по их численности.
В результате этого отождествления от множеств, принадлежащих одному классу эквивалентности, абстрагируется их общее свойство, характеризующее этот класс, в виде самостоятельного понятия — натурального числа.
Название «количественная теория» связано с тем, что в этой теории натуральное число обозначает количество элементов множества.
Достоинством этого подхода является естественное, отражающее основной круг практических применений сложение, вычитание и умножение натуральных чисел.
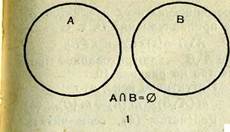
I. Если ЛПВ=0, то т(ЛиВ) = т(Л) + т(В), (1)
т. е. если Л и В — конечные непересекающиеся множества, то число элементов объединения этих множеств равно сумме чисел их элементов (см. рис. 9, /). Сложение чисел абстрагируется от объединения множеств, что и используется в обучении детей дошкольного возраста.
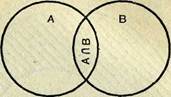
Если же множества Л и В пересекающиеся, т. е. А (рис. 9, 2), то нетрудно заметить, что
так как в сумме т (А) + т (В) число элементов пересечения т. (Л (]В) учитывается дважды: один раз в числе т (Л), второй раз в числе т
Равенство (1), если читать его справа налево, может служить определением суммы двух натуральных чисел:
суммой натуральных чисел а и b называется число а + Ь —
= т(Л11В), где Л и В — произвольные конечные множества такие,
что т(Л) = а, т(В) = Ь и ЛПВ=0. (3)
II. Пусть теперь Л и В — два произвольных конечных множества, причем В^А (рис. 10).
Разность множеств Л и В, обозначаемая А\В, есть множество,
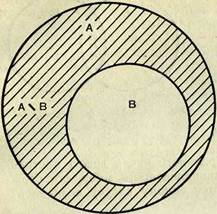 |
состоящее из всех элементов А, не принадлежащих В, т. е. А\В = и х£В), где А\В — заштрихованное множество на рисунке 10.
| Рис. 10. |
Равенство (4), если . читать его справа налево, служит основой для определения разности двух натуральных чисел: разность двух натуральных чисел а и Ь, где а ^ Ь определяется равенством а — Ь — т(А\В), где А а В — произвольные конечные множества, удовлетворяющие условиям
III. Выше (глава IV, § 2) мы видели на примерах, что число
элементов декартового произведения АХВ двух конечных множеств
А а В можно сосчитать как число клеток соответствующей
III таблицы пар. Так, в примере I число элементов множества А
(городов) — 8, а число элементов множества В (рек) — 4, а следо-
111 вательно, множество всевозможных пар (город, река), т. е. эле-
ментов АХВ или клеток таблицы,— 32.
Известно, например, что поля шахматной доски обозначаются парами элементов двух множеств А = и В = 2, 3, 4, 5, 6, 7, 8>, т. е. каждое поле можно рассматривать как элемент декартового произведения Л X В и, так как т (Л) = 8, и т(В) = 8, то т(ЛхВ)=64, т. е. т(А) т(В).
Обобщая эти конкретные случаи, получаем:
Равенство (6) может служить определением произведения двух
где Л и В — произвольные множества, удовлетворяющие условиям т(А) = а и т(В) = Ь.
Из данного определения можно получить другое, сводящее умножение к сложению одинаковых слагаемых. Достаточно считать клетки таблицы или пары, расположенные в прямоугольной таблице, рядами. В каждом ряду m (Л) клеток, а рядов столько, сколько элементов в множестве В, т. е. т (В). Значит, всего клеток т(А)-\
Л эта сумма равна т(АХВ). Но согласно приведенному выше определению m
Если применить этот способ образования или подсчета пар к приведенному выше примеру именования полей шахматной доски,
| a8, |
| e. |
cB, dB, e8, fB, gB, hB,.m(A)
Далее мы обратимся еще раз к описанной выше концепции натурального числа, когда будет возможность сравнить ее с другой, разработанной в математике порядковой теорией натуральных чисел с целью выяснения наиболее приемлемой и целесообразной методики обучения.
studopedia.org — Студопедия.Орг — 2014-2019 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.004 с) .
Натуральное число с точки зрения количественной теории это
В школах РФ действуют учебники по математике (5 кл.), где число нуль не считается натуральным числом, а последствия такого утверждения устраняются дополнительными пояснениями: при отсутствии какогонибудь разряда в записи многозначного числа пишется число нуль. Или же в литературе для старших классов говорится: ряд натуральных чисел расширяется присоединением к нему числа нуль. В дальнейшем число нуль считается целым, рациональным, действительным, комплексным числом.
Другими словами, возникает вопрос: почему число нуль, относясь к целым числам, не является натуральным. По какой причине? Почему число 1 натуральное, а число 0 не натуральное?
Вникнем в сущность понятия «натуральное число». Число 1 свидетельствует о наличии одного элемента в множестве независимо от его реального содержания (человек, птица, яблоко и т.д.). Число 0 свидетельствует об отсутствии какогонибудь элемента в том или ином множестве. И число 1, и число 0 характеризуют то, что имеется 1 элемент или же отсутствует такой элемент в рассматриваемом множестве. В этом смысле эти числа являются «продуктами» одного и того же рода мышления, одного вида рассуждений.
Слово «натура» [4. С. 397] поясняется, как: «1) то же, что и природа; 2) то, что существует в действительности, настоящее». Следовательно, и число 1, и число 0 характеризуют данное множество наличием или отсутствием в нём элементов. В этом смысле они являются натуральными числами, они свидетельствуют о том, какое количество вещей имеется (или не имеется).
В словаре [2. С. 256] разъясняется понятие «конечное множество» — пустое множество, а также всякое множество, равномощное с множеством всяких целых положительных чисел, не превосходящих какогонибудь целого положительного числа».
В математической энциклопедии [3. Т. 2, С. 723] поясняется понятие «кардинальное число» — трансфинитное число, мощность множества по Г. Кантору, кардинал множества А, такое свойство этого множества, которое присуще любому множеству В, равномощному множеству А. Там же, на странице 837 слово мощность поясняется как кардинальное число, а слова «натуральное число» поясняется как кардинальное число [3. Т. 3, С. 892], исключая при этом пустое множество. Здесь мы видим, что имеется некоторое противоречие: мощность множества — кардинальное число, или же кардинальное число — мощность множества, мощность конечного множества — это натуральное число, а пустое множество относится к конечным. Такое противоречие устраняется в логическом словаре [2. С.375]: «Индуктивно натуральное число определяется следующим образом:
1. 0 является натуральным числом.
2. Если п — натуральное число, то и n´ -натуральное число(n=n+1).
3. Никаких натуральных чисел, кроме тех, которые получаются согласно 1 и 2, нет.
4. Для любого натурального числа n существует п´≠0».
Г.В. Дорофеев пишет [1. С. 6769]: «. в рамках теоретикомножественного подхода утверждение, что «0 не является натуральным числом», неверно, а «расширение» множества натуральных чисел с помощью нуля некорректно». Свое мнение по этому вопросу он завершает фразой: «Трактовка нуля как натуральное число одновременно и удобна для математики, и естественно «склеивает» два основных подхода к понятию натурального числа. Кроме того, учащимся согласиться с этим пониманием числа 0 значительно проще, чем многим учителям, уже привыкшим к такому толкованию этого понятия».
Х.Ш. Шихалиев (автор данной статьи), занимающийся вопросом совершенствования содержания и методов обучения математике в общеобразовательной школе (511 классы), начиная с 70х годов прошлого века, и разработавший всю линию обучения математике на теоретикомножественной основе, утверждает не только целесообразность реализации двух подходов к изучения числа в школе, но и необходимость сближения учения о числе в школе к его научной трактовке.
С точки зрения диалектики возникновения и развития понятий «количественная и порядковая теории числа не являются различными, независимыми друг от друга аспектами, а представляют две стороны единого эволюционного процесса развития этого понятия. Каждая из этих теорий разъясняет и дополняет содержание понятия, раскрывая его суть шире, полнее и яснее. Натуральное число появляется как мощность конечного множества, а множество натуральных чисел в целом характеризуется и кристаллизуется как единое целое с помощью теории порядкового числа. Когда теория порядкового числа не в состоянии развить учение о числе дальше, мы общаемся к теории кардинального числа для сравнения различных бесконечных множеств по их мощностям» [6. С. 5354].
Это единство обеих теорий обосновывается в книге И. К. Андронова и А. К. Окунева «Арифметика рациональных чисел». О единстве теорий кардинального и порядкового числа можно найти и у Д. Гильберта. Общность обеих теорий заключается в том, что, с одной стороны, ни одна теория в отдельности не в состоянии раскрыть и развить понятие натурального числа полностью и в совершенстве. С другой стороны, их чередование в обосновании и развитии этого понятия полностью раскрывает инвариантность одной теории с инвариантностью другой, то есть понятие мощности становится результатом счёта и наоборот. По утверждению Фройденталя Г., различие заключается лишь в историческом плане, то есть в том, что «количественное число — совершенно примитивное понятие, которое в развитии человечества было вскоре заменено более тонким»[5. С. 116].
Таким образом, понятия «натуральное число» и «множество натуральных чисел» становятся понятными и логически завершенными только в совместном рассмотрении кардинального и порядкового подходов к ним, а не в раздельном их изучении. Первая теория поясняет содержательную сторону понятия числа, оперируя конкретными множествами, вторая теория усовершенствует математическую сторону понятия, отвлекаясь от его содержательной стороны, возвышая это понятие на новую ступень абстракции. Затем снова возвращается к теории кардинального числа, разъясняя содержательную сторону трансфинитных чисел. В таком подходе к этому понятию чётко видно философское разъяснение природы развития понятий. Такая позиция придерживается многими учеными и педагогами, в частности А.П. Менчинской.
Разработанные учебноэкспериментальные материалы [7, 8, 9, 10] и прошедшие апробацию неоднократно в VXI классах не продвигаются за пределами региона, ссылаясь на то, что МОиН РФ запретило заниматься по учебным пособиям, не имеющим их гриф. Нашим пособиям ранее такой гриф не давали по причине, что их содержание выходит за пределы имеющихся стандартов. Теперь «Новое поколение стандартов образования» стало ближе к нашим позициям. Можно надеяться на то, что наши пособия станут доступными для массового учителя математики. Более того, вопрос о числе нуль возник изза того, что учащийся, считавший запись: 0eN- истинным высказыванием, получил низкий балл, а другой учащийся, считавший эту запись ложным высказыванием, получил на балл выше. Выходит, что быть ближе к науке иногда вредно.
1. Дорофеев Г.В. Математика для каждого. М.: АЯКС, 1999. — 390 с.
2. Кондаков Н.И. Логический словарь. Справочник. М.: Наука, 1976. — 717 с.
3. Математическая энциклопедия. М.: Сов.энциклопедия, 1979.
4. Ожегов СИ., Шведова Н.Ю. Толковый словарь русского языка. М.: РАН, 2009. — 940 с.
5. Фройденталь Г. Математика как педагогическая наука. 4.1.- М.: Просвещ., 1982, 208 с.
6. Шихалиев Х.Ш. Об альтернативном подходе к разработке школьных курсов математики. Махачакала: ДГПУ, 2010. — 196 с.
7. Шихалиев Х.Ш. Математика 56. Учебное пособие. -Махачкала: ДГПУ, 1997. — 246 с.
8. Шихалиев Х.Ш., Алиев Р.Г. Математика 1011. Пробное учебное пособие. — Махачкала: Лотос, 2007. — 160 с.
9. Шихалиев Х.Ш. Алгебра 79. Учебное пособие. — Махачкала: Лотос, 2007. — 256 с.
10. Шихалиев Х.Ш. Геометрия на плоскости 59. Учебное пособие. Махачкала: ДГПУ,1997. — 344 с.
Основные идеи количественной теории натуральных чисел
| страница | 34/128 |
| Дата | 13.10.2018 |
| Размер | 3.28 Mb. |
- Навигация по данной странице:
- А, В, С
- http://studopedia.ru/18_149_teoretiko-mnozhestvenniy-smisl-naturalnogo-chisla-i-nulya.html
- http://vuzlit.ru/899695/teoretiko_mnozhestvennyy_smysl_naturalnogo_chisla_nulya
- http://lechenie-zreniya.ru/zrenie/naturalnoe-chislo-s-tochki-zreniya-kolichestvennoj-teorii-eto/
- http://life-prog.ru/1_32242_opredelenie-naturalnogo-chisla-i-chislo--v-kolichestvennoy-teorii.html
- http://studfiles.net/preview/5473515/page:72/
- http://studbooks.net/1822042/pedagogika/kolichestvennye_naturalnye_chisla
- http://studopedia.org/1-100238.html
- http://top-technologies.ru/ru/article/view?id=26231
- http://zodorov.ru/matematicheskogo-razvitiya.html?page=34