Алиса в стране чудес с точки зрения математики

Рассмотрим на чем были основаны приключения Алисы.

Доджсон находил новую математику нелогичной. В «Алисе» он выступил против некоторых идей как против чуши, в том числе против символической системы алгебры. Слово
Во фрагменте с Гусеницей Алиса подвергается чудовищной форме «альджебр аль мукабала». Сначала она пытается «восстановить» себя до ее первоначального, большого, размера, но заканчивает «уменьшением», причем так быстро, что ударяется подбородком об ногу.

Она думает: «Быть такой разноразмерной за один день — очень стеснительно». «Нет, не так» — отвечает Гусеница, появляющаяся из безумного мира символической алгебры.

Она советует Алисе оставаться пропорциональной, даже если она не сможет «держаться в едином размере хоть 10 минут!» Пропорциональность, а не абсолютный размер — вот что имело значение в наземном мире Евклидовой геометрии.

В алгебраическом же мире, конечно же, это не так легко. Алиса съедает немного грибов, и её шея изгибается, как змея, раздражая голубей. Однако она находит способ ужать себя до девяти дюймов.

В главе «Свинья и перец», когда Алиса выносит ребёнка Герцогини из дома, и он становится поросёнком, автор пародирует принцип преемственности, который был введён в середине 19 века во Франции.

Безумный Шляпник и Мартовский Кролик защищают математику Гамильтона, одного из великих инноваторов в Викторианской алгебре. В заголовке седьмой главы, «Сумасшедшее чаепитие», мы должны читать «tea-party» как «t-party», с буквой t, которая обозначает время в математике.

Доджсон заставил Шляпника, Кролика и Соню ходить вокруг да около чайного столика, чтобы продемонстрировать кватернионы — численную систему, основанную на четырёхмерном Евклидовом пространстве.

В 1860-х годах кватернионы были провозглашены последним серьёзным шагом в расчётах движения. Даже Доджсон считает их гениальным инструментом для прогрессивных математиков, но все, же они раздражали и запутывали многих студентов, таких, как Алиса.

На сумасшедшем чаепитии, время — отсутствующая четвертая сущность за столом. Шляпник говорит Алисе, что он поссорился со Временем и теперь «оно не станет делать ничего, о чем я попрошу».

Потому Шляпник, Кролик и Соня (третье «измерение») вынуждены вечно кружиться в плоскости вокруг стола.

Математика придает «Алисе» таинственности и превращает ее в некого рода загадку, которая может развлечь человека в любом возрасте уже не один век.

Политех к 150-летию сказки открыл в павильоне «Оптика» на ВДНХ интерактивную выставку «Алиса в Стране наук», которая раскрывает суть явлений, описанных в книге, с точки зрения науки. «Афиша» разобралась, где же в сюрреалистической сказке искать науку.

Чарлз Доджсон, математик из колледжа Крайст-Черч Оксфордского университета, впервые рассказал фантастическую историю про девочку, которая попадает сквозь кроличью нору в воображаемый мир, дочерям своего коллеги — декана Генри Лидделла. Они сплавлялись на лодке вниз по Темзе, и 10-летняя Элис Лидделл уговорила Доджсона записать эту сказку — в итоге математик послушался ее совета, взял литературный псевдоним Льюис Кэрролл и создал один из лучших образцов литературы в жанре абсурда, в котором вот уже 150 лет находят вдохновение художники, музыканты и ученые.

«Конечно, при достаточно буйной фантазии можно с любым произведением сделать что угодно. Но «Алису» мы взяли не просто так: многие физики, биологи используют понятия из сказки. Некоторые делают это прямо, как например, с гипотезой Черной королевы (у нас есть немного об этом на выставке). Физики любят эту сказку и сравнивают расширяющуюся Вселенную с растущей Алисой, астрофизик Артур Эддингтон сравнивал хливких шорьков с элементарными частицами. Алиса постоянно, на каждом шагу, встречала что-то «мозгоразрывное» — то, что переворачивало все привычное для нее. То же самое происходит с ученым. Чтобы совершить открытие, ему нужно уйти от всего привычного и обратиться к тем областям, которые находятся на грани понимания. Взять, к примеру, квантовую механику… Да что там! Даже современная биология, которая сплошь состоит из статистики, — Страна чудес, где постоянно приходится испытывать переворот у себя в голове: «Как? Почему?»

• 

В 1960-х, во время расцвета психоделической революции, книгу стали интерпретировать по-новому: различные магические зелья, гриб, меняющий физическое состояние, гусеница, курящая кальян, да и вся атмосфера сказки, которая была написана в эпоху законного использования опиума, казалась одним красочным описанием наркотического трипа. В 1967 году группа Jefferson Airplane выпустила песню «White Rabbit» с отсылками к книге, которая впоследствии стала гимном психоделической культуры. Однако эксперты по творчеству Кэрролла, как правило, скептически относятся к таким трактовкам. Нет никаких сведений о том, что Кэрролл употреблял опиум или какие-либо другие наркотики. «Идея о том, что сюрреалистические аспекты текста подпитывались употреблением наркотических средств, резонирует с культурой, в частности, 60-х, 70-х и 80-х годов, когда широкое распространение получили психоделики», говорит доктор Хизер Уортингтон в интервью BBC.

Чтобы докопаться до более правдоподобной интерпретации произведения, стоит вспомнить, что происходило в науке во второй половине XIX века, когда профессор Доджсон писал свою сказку. Это был период бурного развития математики, когда ее субъект становился все более абстрактным. Появление неевклидовой геометрии, развитие абстрактной алгебры, повсеместное использование «воображаемых чисел» — это лишь некоторые открытия, которые потрясли саму суть дисциплины. Доджсон придерживался довольно традиционных взглядов на математику, которая строилась прежде всего на аксиоматическом подходе Евклида. Возможно, потому, что он не занимался исследованиями, а лишь преподавал дисциплину, он сыскал славу «упрямого консервативного математика», который в развитии видел лишь снижение требовательности к научному знанию. И его «Алису в Стране чудес» в какой-то степени можно назвать злой сатирой на то, что происходило в математике на тот момент.

В журнале New Scientist была опубликована работа оксфордского математика Мелани Бейли («Alice’s Adventures in Algebra: Wonderland Solved»), в которой она проводит параллели между сюжетом сказки и критикой абстракции в математике. По теории Бейли, все безумное волшебство, которое происходит в «Алисе», — это описание того опасного хаоса, который несла новая символьная алгебра, с точки зрения Доджсона.

Алиса из рационального мира попадает в страну, где даже числа ведут себя хаотично. В коридоре она пытается вспомнить таблицу умножения: умножив 4 на 5 и на другие числа, она все время получает меньше 20. «А ну-ка проверю, помню я то, что знала, или нет. Значит, так: четырежды пять — двенадцать, четырежды шесть — тринадцать, четырежды семь… Так я до двадцати никогда не дойду! Ну, ладно, таблица умножения — это неважно!»

Приключения Алисы в алгебре: ответы на загадки Страны Чудес

А что если автор «Алисы в Стране чудес» вовсе и не заступал в долины подсознательного в своем произведении, а просто выразил свое отношение к современным ему процессами в математической науке таким вот необычным и замысловатым образом? Все-таки он был преподователям Царицы наук, а не психиатором. Читаем и решаем сами, согласиться ли с автором поста или все-таки, по старинке, с группой Jefferson Airplane.

Так сказка или все-таки сатира против современников-математиков?

Знаменитая «Алиса в стране чудес» Льюиса Кэрролла была бы совсем другой книгой без Чеширского Кота, описания суда, «ребёнка» Герцогини и без Безумного Чаепития в компании Болванщика. Однако, если познакомиться с оригиналом той сказки, которую автор рассказал Алисе Лиддел и двум ее сестрам однажды на лодочной прогулке близ Оксфорда, то вы не найдете в тексте всех этих знаменитых персонажей и символов.

Когда я взялась за написание диссертации, посвящённой английской литературе викторианской эпохи, я хотела выяснить, что вдохновило автора на все эти более поздние дополнения. В критической литературе книга, как правило, интерпретируется во фрейдистском ключе как стремительный спуск в темные глубины подсознания. Подробный анализ добавленных сцен мне не попадался, но одна работа сильно выделялась на фоне остальных. В 1984 году Хелена Пайсиор из университета Висконсин-Милуоки написала статью, в которой проследила связи между судом над Червонным Валетом с викторианским учебником алгебры. Учитывая основную специальность автора «Алисы», было довольно удивительно обнаружить, что почти не существует исследований его книги с математической точки зрения. Как известно, «Кэрролл» – это псевдоним. Настоящее имя автора – Чарльз Доджсон, он работал преподавателем математики в оксфордском колледже Крайст-Чёрч.

Для математики XIX век выдался очень бурным, породил множество новых и неоднозначных концепций, которые, однако, были широко восприняты в научном сообществе. Если рассмотреть «Алису в стране чудес» именно в таком контексте, становится понятно, что математик Доджсон, отличавшийся редкостным консерватизмом, придумал некоторые сцены, отсутствующие в первой редакции сказки, чтобы высмеять эти радикально новые идеи.

Даже самые восторженные поклонники Доджсона вынуждены признать, что тот был очень осторожным математиком и оставил совсем мало оригинальных работ. Однако он был добросовестным педагогом и из всех математических работ превыше всего ценил древнегреческий евклидовский трактат «Начала», который считал образчиком математического мышления. В целом этот труд Евклида посвящён геометрии окружностей, четырёхугольников, параллельных прямых, а также затрагивает простейшие тригонометрические функции. Но самая поразительная черта «Начал» заключается в исключительной строгости рассуждений. Евклид начинает книгу с изложения нескольких неопровержимых истин (аксиом), а затем выстраивает на их основе сложные доказательства. При этом каждый шаг доказательства остается простым и логичным. Каждая посылка постулируется, доказывается, а каждая такая теорема резюмируется «Что и требовалось доказать».

Веками такой подход считался вершиной математического и логического мышления. Однако, к разочарованию Доджсона, не все математики его века отличались евклидовской скрупулёзностью. Доджсон отвергал их работы как «полудилетантские» и даже считал не вполне логичными. Тем не менее, к разочарованию Доджсона, эта новая математика все сильнее отдалялась от физической реальности, на основе которой были построены труды Евклида.

В настоящее время ученые широко используют математические концепции, которые на первый взгляд кажутся нелогичными, например, мнимые числа. Мнимое число представляет собой квадратный корень из отрицательного числа и описывает физические величины совсем не так, как целые числа или дроби. В викторианскую эпоху еще никто не воспринимал эти новые концепции безоговорочно, шли отчаянные поиски философской базы, которую можно было бы подвести под эти феномены. Однако такие разработки открывали перед математиками удивительные возможности для исследования новых идей. Многие были готовы вооружиться этой странной логикой, поскольку существовал вполне непротиворечивый научный аппарат для операций над такими концепциями. Тем не менее, с точки зрения Доджсона, новая математика была абсурдна. Он признавал, что все эти наработки могут быть интересны маститому ученому, но был уверен, что все это невозможно объяснить обычному студенту.

В научной периодике Доджсона просто разгромили, и он решил подойти к математике через художественную литературу. Вооружившись методом, знакомым из доказательств Евклида – доведением до абсурда, – он раскритиковал «полулогичность» новой математики. Доджсон высмеял ее слабые стороны, доведя заложенные в ней посылки до логического завершения и ожидаемо получив абсурдные результаты. Так появилась книга «Алиса в стране чудес».

Алгебра и кальян

Обратимся, например, к главе «Синяя гусеница даёт совет». Алиса уже успела упасть в кроличью нору и съесть пирожок – в том эпизоде девочка уменьшилась до трёх дюймов. А в пятой главе, которую мы решили перечитать, автор знакомит нас с Гусеницей, которая курит кальян. Гусеница показывает Алисе гриб: чтобы вернуть нормальные размеры, девочке нужно им полакомиться. Но вся загвоздка в том, что мякоть с одной стороны гриба вытягивает Алисину шею, а с другой стороны – укорачивает туловище. Чтобы вернуть себе нормальные размеры и пропорции, Алиса должна откушать строго определенное количество мякоти с каждой стороны гриба.

Некоторые исследователи считают, что эта сцена с кальяном и «волшебным грибом» намекает на наркотики. Однако, я полагаю, здесь Доджсон излагает свои представления об абсурдности символической алгебры, которая разрывала связи между алгеброй, арифметикой и излюбленной геометрией Доджсона. В следующих главах книги содержатся более специфические математические аналогии, но эта сцена легкая и игривая. Она задает тон для того сюра, который ждет читателя впереди.

Первый намёк может быть связан с самим кальяном: начнем с того, что в английском языке кальян называется словом «hookah», которое имеет арабское происхождение, как и слово «алгебра». Тем более интересно отметить, что Огастес де Морган, первый британский математик, сформулировавший непротиворечивый аппарат правил символической алгебры, использует в своей книге «Тригонометрия и дважды алгебра» (1849) оригинальное арабское название алгебры. Морган употребляет формулировку «al jebr e al mokabala» [аль джебр э аль мокабала], что означает «сокращение и восстановление» – фактически, именно это и претерпевает Алиса. Именно стремление к «восстановлению» привело Алису к грибу: она искала, чего бы такого съесть или выпить, чтобы приобрести нормальный размер. Когда она съела кусочек гриба, с ней произошло как раз «сокращение» – подбородок стукнулся о ноги.

В своей работе де Морган описывает, почему хочет отойти от универсальной арифметики, где алгебраические символы означают конкретные числа, соответствующие физическим величинам. Он предпочитает такой системе символическую алгебру, где допускаются любые «абсурдные» операции, в том числе, приводящие к отрицательным или невозможным решениям. Главное, чтобы эти операции следовали четкой внутренней логике. Именно символическая алгебра сегодня стала отточенным языком для описания отношений между математическими объектами, но в викторианскую эпоху алгебра воспринималась совершенно иначе. В первых работах по символической алгебре также сохранялась косвенная связь с физическими величинами.

Де Морган желал устранить даже эту зыбкую связь с измерениями и предлагал трактовать символическую алгебру как грамматическую систему. Достаточно «сократить» алгебру от универсальной арифметики до набора логических, но при этом совершенно символических операций, считал он, и мы сможем «восстановить» более глубокий смысл всей системы. Правда, на тот момент он ещё не мог сказать как.

Алиса, держи себя в руках

Я полагаю, что абсурдность Страны Чудес отражает представления Доджсона об опасностях новой символической алгебры. Алиса попадает из рациональной реальности в мир, где даже числа действуют беспорядочно. В зале, куда ее привела кроличья нора, Алиса пытается припомнить таблицу умножения, но оказывается, что ее расчёты не вписываются в привычную систему с основанием 10. В сцене с гусеницей Доджсон выражает свои опасения, рассказывая, что Алисин рост колеблется между 9 футами и 3 дюймами. Алиса скована рамками традиционной арифметики, где физическая величина (например, размер) должна быть определенной. Алису это сильно беспокоит. «Столько превращений в один день хоть кого собьет с толку», – жалуется она. «Не собьет», – возражает Гусеница. Действительно, она же привыкла жить в абсурдном мире.

Предостережение, которое Гусеница изрекает в конце этой сцены, вероятно, один из самых красноречивых намеков на доджсоновкую консервативную математику. «Держи себя в руках!» – заявляет Гусеница. Алиса предполагает, что Гусеница рекомендует ей не злиться. Однако, хотя девочка действительно выражается достаточно резко, к этому моменту она не успела сказать ничего обидного, поэтому достаточно странно, что совет Гусеницы звучит именно так. В оригинале же гусеница говорит: «Keep your temper». Интеллектуалы времен Доджсона, вероятно, должны были понять слово «temper» (умеренность) в буквальном смысле: «пропорция, где все свойства находятся в правильном соотношении». Таким образом, Гусеница подсказывает Алисе, что сохранять умеренность – это придерживаться правильных пропорций, независимо от того, каков твой размер.

Здесь, опять же, прослеживается любовь Доджсона к евклидовой геометрии, где абсолютная величина не имеет значения. По-настоящему важны лишь соотношения длин отрезков, например, при определении свойств треугольника. Чтобы уцелеть в Стране Чудес, Алиса должна действовать, как геометр-евклидианец, – сохранять пропорции, даже если её размеры меняются.

Разумеется, она этого не делает. Алиса съедает кусочек гриба, и её шея вырастает, как у змеи, что приводит к новому витку абсурда, пока Алиса не исправляет свой рост, откусив от гриба с другой стороны. Это важная присказка для следующей главы «Поросёнок и перец», где Доджсон пародирует еще один тип геометрии.

К этому моменту Алиса уже вернулась к своим нормальным размерам, но затем девочка снова уменьшается, чтобы попасть в маленький домик. Там на кухне она встречает Герцогиню, баюкающую ребёнка. Кухарка сыплет в суп слишком много перца, и от запаха супа чихают все, кроме Чеширского Кота. Но когда Герцогиня даёт Алисе подержать ребенка, тот почему-то превращается в поросенка.

Весь этот эпизод посвящён проективной геометрии, которая исследует свойства фигур. Эти свойства не изменяются, даже если фигура проецируется на другую плоскость. Допустим, изображение выводится на подвижный экран, а затем мы наклоняем этот экран под разными углами, получая семейство фигур. В этой дисциплине присутствуют различные феномены, многие из которых Доджсон, вероятно, считал нелепыми. Типичным примером такого феномена является «принцип непрерывности».

Жан-Виктор Понселе, математик, предложивший этот принцип, формулирует его следующим образом: «Если одна фигура получается из другой непрерывным преобразованием и полученная фигура не уступает по общности исходной, то можно сразу же утверждать, что любое свойство первой фигуры будет справедливо и для второй фигуры».

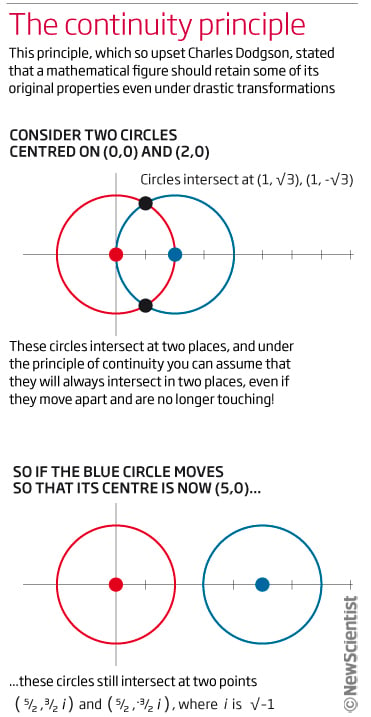
Пожалуй, простейшим примером этого принципа является соотношение двух пересекающихся окружностей. Решив их уравнения, мы найдем, что они пересекаются в двух разных точках. Согласно принципу непрерывности, любое непрерывное преобразование этих окружностей, например, удаление их центров друг от друга, не нарушает вышеуказанного базового свойства, а именно: окружности так и будут пересекаться ровно в двух точках. Лишь если центры окружностей будут удалены друг от друга достаточно сильно, решение задачи будет включать мнимое число, которое нельзя выразить в «физическом» смысле.

Разумеется, когда Понселе говорит о «фигурах», он имеет в виду геометрические фигуры. Но в английском языке слово «figure» также означает «персонаж», и Доджсон шутливо подвергает «полудилетантский» аргумент Понселе строгому логическому анализу, доводя его до самого абсурдного вывода. Если принцип действует на треугольники, значит, он должен действовать и на младенцев. Если нет – сам принцип является ошибочным. Что и требовалось доказать. Итак, Доджсон превращает младенца в поросенка в соответствии с принципом непрерывности. Примечательно, что это существо сохраняет большую часть своих основных черт, что полностью согласуется с принципом непрерывности. Например, его ручки и ножки по-прежнему торчат в разные стороны, как лучи морской звезды, малыш все изгибается, нос у него слишком вздернутый для младенца, а глазки – слишком маленькие. Алиса осознает, что произошло, только когда плач младенца сменяется хрюканьем. Все происходящее доставляет малышу огромное неудобство, а несдержанная жестокость Герцогини ярко демонстрирует ядовитый скепсис Доджсона относительно «современной» проективной геометрии. В главе о поросёнке и перце абсолютно всё идет наперекосяк. Герцогиня – плохая аристократка и никуда не годная мать, Кухарка – плохая повариха, которая задымляет всю кухню, переперчивает суп и, в конце концов, начинает бросаться кочергой, горшками и тарелками.

Алису злит вся эта кутерьма, она покидает дом Герцогини и отправляется на чаепитие к Болванщику. Здесь автор препарирует работы ирландского математика Уильяма Роуэна Гамильтона. Гамильтон умер в 1865 году вскоре после публикации «Алисы в стране чудес». Но в тот период всё ещё широко обсуждалось открытие кватернионов, сделанное Гамильтоном в 1843 году. Это открытие считалось важнейшей вехой в истории абстрактной алгебры, поскольку кватернионы обеспечивали алгебраическое вычисление вращений.

Как известно, комплексное число состоит из двух частей. Кватернионы существуют в такой математической системе, которая основана на использовании четырех частей (см. «Мнимая математика»). Гамильтон долгие годы разрабатывал трехчастную систему – по одной части на каждое пространственное измерение, – но ему удавалась лишь модель вращения на плоскости. Но, когда он добавил четвертую часть, удалось, наконец, представить трехмерное вращение. Правда, Гамильтон затруднялся описать, чему же соответствует дополнительная четвертая часть. Как и большинство викторианцев, он был уверен, что эта часть должна что-то означать. Поэтому в предисловии к своим «Лекциям о кватернионах» (1853) он сделал примечание: «Мне казалось (и по-прежнему кажется) естественным соотнести эту внепространственную часть с феноменом времени».

Гамильтон полагал, что если геометрия обеспечивает исследование пространства, то алгебра, в свою очередь, позволяет изучать «чистое время». Это довольно запутанная концепция, которую Гамильтон сформулировал на основе идей Канта. Предполагалось, что «чистое время» представляет собой идеал времени в платоновском смысле и отличается от реального времени, воспринимаемого людьми. Другие математики вежливо, но осторожно относились к этой гипотезе, считая, что «идеальное время» – это уже слишком. Между математикой Гамильтона и чаепитием у Башмачника прослеживаются поразительные параллели. Алиса сидит за столом с странными персонажами: Болванщиком, Мартовским Зайцем и Мышью-соней. Персонаж Время, который поссорился с Болванщиком, отсутствует. Но из вредности Время не позволяет стрелкам часов Болванщика дойти до шести вечера и продвинуться дальше.

Если интерпретировать эту сцену в контексте математики Гамильтона, можно сделать вывод, что трое персонажей соответствуют трем частям кватерниона, а важнейшая четвертая часть – Время – отсутствует. Автор объясняет нам, что без Времени вся троица навечно застряла за чаепитием, и они «даже посуду мыть не успевают».

Их суета вокруг стола напоминает о первых попытках Гамильтона вычислить движение, которое сначала (до добавления в систему четвертой части – Времени) удавалось смоделировать лишь на плоскости. Даже когда Алиса присоединяется к чаепитию, она не может остановить возню Болванщика, Зайца и Сони, так как девочка не является внепространственной единицей, подобной Времени.

В этой сцене Болванщик загадывает абсурдную загадку: «Чем ворон похож на конторку?» Этот эпизод более чётко указывает на теорию «чистого времени». Гамильтон утверждал, что на уровне чистого времени исчезает связь между причиной и следствием, и, возможно, именно на это указывает безумность загадки Болванщика, на которую не может быть ответа. Алиса смело пытается отгадать загадку, и здесь автор высмеивает еще одно свойство кватернионов. Дело в том, что умножение кватернионов некоммутативно, то есть, x × y не равно y × x. Ответы Алисы также некоммутативны. Когда Заяц заявляет, что «нужно всегда говорить то, что думаешь», Алиса отвечает: «Я так и делаю… По крайней мере, я всегда думаю, что говорю… а это одно и то же». «Совсем не одно и то же!, – возражает Болванщик. – Так ты еще, чего доброго, скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу» – одно и то же». Вероятно, подобные идеи должны были раздражать математика-консерватора наподобие Доджсона, поскольку некоммутативная алгебра противоречит основополагающим законам арифметики и открывает удивительный мир новой математики – даже еще более абстрактный, чем тот, который описали сторонники символической алгебры.

В финале этой сцены Болванщик и Заяц засовывают Соню в чайник. Возможно, это путь к свободе. Если бы парочка смогла избавиться от Сони, то могла бы существовать независимо – как двухчастное комплексное число. Это тоже безумие, считает Доджсон, но тогда, по крайней мере, можно будет не двигаться кругами вокруг стола (то есть, не вращаться).

Здесь, вероятно, сатирические выпады Доджсона против современников-математиков заканчиваются. Что же остается в сказке «Алиса в стране чудес» без этих аналогий? Ничего кроме исходной доджсоновской сказки на ночь «Приключения Алисы под землей». Эта сказка очаровательна, но совершенно лишена всякого характерного нонсенса. Доджсон демонстрирует верх остроумия именно когда высмеивает что-либо, но он пускается в сатиру, лишь если тема донельзя его задевает. Он написал два уморительно смешных памфлета, в которых ерничал над новыми порядками в Оксфордском университете. Напротив, все его истории, кроме «Алисы», были скучны и нравоучительны.

Готова поспорить, что не будь в «Алисе» яростной сатиры, с которой Доджсон обрушился на своих коллег-математиков, эта книга никогда не стала бы такой знаменитой, а Льюиса Кэрролла никто бы не помнил как непревзойденного мастера сюрреалистической сказки.

Алиса в стране чудес с точки зрения математики

Погнавшись за Белым Кроликом, Алиса провалилась в колодец и полетела вниз. Но почему именно вниз? Что за сила влекла ее? Сила собственной тяжести — это раз. Но кроме Алисы в этой истории задействовано куда более массивное тело — наша планета.

Великий ученый Исаак Ньютон понял, что все тела притягиваются друг к другу. Именно эта сила удерживает Луну на орбите нашей планеты и не дает ей улететь в открытый космос. Эта же сила заставляет яблоко падать на землю, а Алису лететь вниз в колодце.

Ньютон назвал эту силу термином тяготение , или гравитация — от слова gravis . Но какова ее природа, понять не смог.

Только в начале ХХ века Альберт Эйнштейн догадался, откуда она берется. Согласно его общей теории относительности, всякое тело искривляет пространство вокруг себя, и именно это искривление мы ощущаем как земное притяжение.

При этом сама Алиса, падая, не ощущает притяжения, и если она закроет глаза, то может подумать, что парит в невесомости.

Уменьшение Алисы с точки зрения биологии

Алиса — человек, следовательно, она млекопитающее. Млекопитающие теплокровны, а значит, температура их тела не зависит от температуры окружающей среды. До каких размеров Алиса могла бы уменьшиться, сохраняя теплокровность?

Самые маленькие млекопитающие на Земле — карликовые многозубки. Они достигают 3 — 4,5 см в длину и весят около 1,7 — 2 граммов. Такое маленькое животное теряет тепло очень быстро. Чтобы компенсировать потери энергии, оно вынуждено съедать за сутки пищи вдвое — втрое больше собственного веса.

Фактически многозубки почти всю жизнь проводят в поисках еды. Для некоторых из них даже двухчасовая голодовка смертельна. Кроме того, для получения энергии необходимо очень много кислорода, переносимого кровью. Поэтому сердце этих животных сокращается 1300 — 1500 раз в минуту!

Множество ничего с точки зрения математики

В математике множество — это любая совокупность объектов, ни один из которых не повторяется. Какие именно объекты входят в множество, не важно: это могут быть буквы, цифры, слова…

Знаменитый математик Леонард Эйлер еще в XVIII веке предложил рисовать множества с помощью кругов. Этот способ стал популярным после выхода книги Джона Венна Символическая логика , потому и называется диаграмма Венна .

Как устроены эти диаграммы? Рассмотрим пример для трех множеств. Каждое из множеств изображается в виде круга, в котором находятся элементы этого множества. Те элементы, которые входят одновременно в два множества, размещаются в общей части двух кругов .

А есть и элементы, которые входят во все три множества, — они находятся в части, общей для всех трех кругов.

Четыре или пять множеств изобразить кругами на диаграмме Венна уже не получится, однако вместо кругов в этом случае можно использовать эллипсы. Попробуйте нарисовать такую диаграмму.

Приглашение к обсуждению прочитанного

Из wikipedia.org

Алиса в Стране чудес, сказка, написанная английским математиком, поэтом и писателем Чарльзом Лютвиджем Доджсоном под псевдонимом Льюис Кэрролл и изданная в 1865 году.

Наука, область человеческой деятельности, направленная на выработку и систематизацию объективных знаний о действительности.

Белый Кролик, персонаж книги Льюиса Кэрролла «Приключения Алисы в Стране чудес».

Алиса, главная героиня книг Льюиса Кэрролла «Алиса в Стране чудес» и «Алиса в Зазеркалье».

Колодец, гидротехническое сооружение для добывания грунтовых вод, обычно представляющее собой вертикальное углубление с укреплёнными стенками и механизм подъёма воды на поверхность

Сила тяжести, сила, действующая на любое физическое тело, находящееся вблизи поверхности Земли или другого астрономического тела.

Невесомость, состояние, при котором сила взаимодействия тела с опорой, возникающая в связи с гравитационным притяжением, пренебрежимо мала.

ПЕРЕЧИТЫВАЯ «АЛИСУ…»

Кандидат педагогических наук Наталья КАРПУШИНА.

Спустя почти полтора столетия после появления на свет сказок Льюиса Кэрролла они живут себе — «живее некуда!» (как сказал бы королевский Гонец Зай Атс). Юная героиня из Страны чудес и Зазеркалья, Алиса думала, что в книжке без картинок и разговоров нет толку. А какой толк в книжке, если в ней нет ни вопросов, ни загадок? Приглядитесь к книжкам об Алисе: ни картин природы, ни описаний героев и их характеров, ни «лирических отступлений» и комментариев автора. Зато что ни эпизод — то задача: математическая, логическая, лингвистическая, да мало ли какая ещё? ! Что ни диалог — то размышления на философскую, историческую или психологическую тему. Что ни вопрос — то повод подумать вместе с героями над новой проблемой и попытаться вникнуть в её суть.

Начнём со сказки «Алиса в Стране чудес». Вспомним эпизоды, где идёт речь о свойствах окружности. Вот два из них.

В огромную лужу слёз, которую наплакала Алиса, попáдали разные птицы и звери. Выбравшись из лужи, они стали искать способ, как побыстрее обсохнуть. По предложению Птицы Додо было решено устроить бег по кругу.

«Сначала он нарисовал на земле круг. Правда, круг вышел не очень-то ровным, но Додо сказал:

— Правильность формы несущественна!

А потом расставил всех без всякого порядка по кругу. Никто не подавал команды — все побежали, когда захотели… Через полчаса, когда все набегались и просохли, Додо вдруг закричал:

Все столпились вокруг него и, тяжело дыша, стали спрашивать:

На этот вопрос Додо не мог ответить, не подумав как следует… Наконец, Додо произнёс:

— Победили все! И каждый получит награды!»*

Математиков в этой истории могли бы заинтересовать три момента.

Во-первых, почему Додо расставил всех по кругу без всякого порядка? Почему бы для точек круга, а вернее окружности, не указать, какая из трёх произвольно взятых точек находится между двумя другими (по аналогии с точками прямой)? Если хотите, имеет ли смысл это делать?

Во-вторых, что именно заставило Додо как следует задуматься? Иначе говоря, почему в беге по кругу не оказалось проигравших, а были одни победители?

И, наконец, что имел в виду Додо, сказав о нарисованной на земле линии: «Правильность формы несущественна»?

О каких свойствах окружности поведал нам автор — математик Чарлз Лютвидж Доджсон, предстающий в этом эпизоде в образе Птицы Додо?

«С ОДНОЙ СТОРОНЫ, С ДРУГОЙ СТОРОНЫ…»

Когда Алиса повстречалась с Синей Гусеницей (та восседала на огромном, ростом с девочку, грибе и томно курила кальян), между ними завязалась беседа, в ходе которой девочка пожаловалась на свой маленький рост.

«— Если вы не возражаете, сударыня, — отвечала Алиса, — мне бы хотелось хоть капельку подрасти. Три дюйма** — такой ужасный рост!

— Со временем привыкнешь, — возразила Гусеница, сунула кальян в рот и выпустила дым в воздух.

Алиса терпеливо ждала, пока Гусеница не соблаговолит снова обратить на неё внимание. Минуты через две та вынула кальян изо рта, зевнула — раз, другой — и потянулась. Потом она сползла с гриба и скрылась в траве, бросив Алисе на прощанье:

— Откусишь с одной стороны — подрастёшь, с другой — уменьшишься!

— С одной стороны чего? — подумала Алиса. — С другой стороны чего?

— Гриба, — ответила Гусеница, словно услышав вопрос, и исчезла из виду.

С минуту Алиса задумчиво смотрела на гриб, пытаясь определить, где у него одна сторона, а где — другая; гриб был круглый, и это совсем сбило её с толку».

Да уж, есть о чём призадуматься!

Ряд эпизодов из сказки «Алиса в Зазеркалье» иллюстрирует идею зеркальной симметрии. В зеркале все асимметричные предметы (а в более широком смысле — любые асимметричные ситуации) предстают обращёнными, или вывернутыми (имеются в виду предметы, во-первых, повёрнутые в пространстве на пол-оборота — 180 градусов; во-вторых, такие, у которых левая и правая половинки поменялись местами). На страницах книги часто встречаются подобные «отражения», к которым Алиса никак не могла привыкнуть и не переставала им удивляться.

ПО ТУ СТОРОНУ ЗЕРКАЛА

Ещё до того как Алиса попала в Зазеркальный дом, у неё было в целом правильное представление о том, как он должен выглядеть:

«— Во-первых, там есть вот эта комната, которая начинается прямо за стеклом. Она совсем такая же, как наша гостиная, Китти, только всё там наоборот! Когда я залезаю на стул и смотрю в Зеркало, она видна мне вся, кроме камина. Ах, как бы мне хотелось его увидеть! Но в это Зеркало, как ни гляди, камина не увидишь… А книжки там очень похожи на наши — только слова написаны задом наперёд. Я это точно знаю, потому что однажды я показала им нашу книжку, а они показали мне свою!

…А дальше идёт коридор. Если распахнуть дверь в нашей гостиной пошире, можно увидеть кусочек коридора в том доме, он совсем такой же, как у нас».

Всё ли так просто и правильно в этом описании, как кажется на первый взгляд? Действительно ли в комнате за стеклом должно быть всё наоборот? И что значит в данном случае наоборот? Почему, стоя по эту сторону зеркала, камина не увидишь, как ни старайся? Всегда ли, поднеся книгу к зеркалу, мы увидим слова, написанные задом наперёд? Или книжку надо поднести каким-то определённым образом? Одним словом, придётся поломать голову.

«ПОЙДУ-КА Я К НЕЙ НАВСТРЕЧУ…»

А помните, как Алиса повстречалась с Чёрной Королевой? Для того чтобы приблизиться к ней, девочке пришлось идти. в противоположном направлении. Читаем в сказке:

«Вон она идет! — закричал молоденький Шпорник.

Алиса радостно оглянулась — и увидела Чёрную Королеву.

— Пойду-ка я к ней навстречу, — сказала Алиса.

— Навстречу? — переспросила Роза. — Так ты её никогда не встретишь! Я бы тебе посоветовала идти в обратную сторону!

— Какая чепуха! — подумала Алиса.

Впрочем, вслух она ничего не сказала и направилась прямо к Королеве. К своему удивлению, она тут же потеряла её из виду и снова оказалась у порога дома.

В сердцах она отступила назад, огляделась по сторонам в поисках Королевы, которую наконец увидала вдали, и подумала: не пойти ли на этот раз в противоположном направлении?

Всё вышло как нельзя лучше. Не прошло и минуты, как она столкнулась с Королевой у подножья холма, куда раньше никак не могла подойти».

Оказывается, пироги в Зазеркалье сначала раздают гостям и только потом режут на части!

«— Что ж, угости нас пирогом, Чудище, — сказал Лев и улёгся на траву, положив подбородок на лапы.

…Алиса сидела на берегу ручейка, поставив большое блюдо себе на колени, и прилежно водила ножом.

— Ничего не понимаю! — сказала она Льву (она уже почти привыкла к тому, что её зовут Чудищем). — Я уже отрезала несколько кусков, а они опять срастаются!

— Ты не умеешь обращаться с Зазеркальными пирогами, — заметил Единорог. — Сначала раздай всем пирога, а потом разрежь его!

Конечно, это было бессмысленно, но Алиса послушно встала, обнесла всех пирогом, и он тут же разделился на три части.

— А теперь разрежь его, — сказал Лев, когда Алиса села на своё место с пустым блюдом в руках».

«ЗАДОМ НАПЕРЁД, СОВСЕМ НАОБОРОТ!»

Для жителей Зазеркалья совершенно естественно, что утолить жажду можно, съев несколько сухариков; что за одно яйцо следует заплатить пять пенсов, а за два — всего два. Чтобы перестала идти кровь из пальца, его надо уколоть булавкой, а чтобы остаться на том же месте, нужно бежать со всех ног. Вспомните, как Белая Королева рассказывает Алисе о преимуществах жизни «в обратную сторону»! Например, в Зазеркалье «завтра никогда не бывает сегодня», а лучше всего обитателям Зазеркалья помнится то, что только случится через некоторое время.

Целая глава в книге посвящена зеркальным близнецам Труляля и Траляля. Кстати, любимое выражение Траляля «Задом наперёд, совсем наоборот!» как нельзя лучше характеризует суть описанных Кэрроллом превращений: зеркало изменяет последовательность, в которой расположены точки на прямой (события во времени), на обратную.

В сказках об Алисе множество загадок и ни одной отгадки, ни одного прямого ответа. Только умело поставленные вопросы и грамотно разбросанные по тексту подсказки, да едва уловимые намёки. Но это тот случай, когда не договорить, а лишь приоткрыть завесу тайны лучше, чем выдать все секреты и поделиться с читателями готовым знанием. Так стоит ли удивляться тому, что творения Льюиса Кэрролла, будучи превосходной пищей для размышлений, и по сей день будоражат пытливые умы? Как и тому, что кто-то вовсе не воспринимает тонкую интеллектуальную игру писателя? «Алиса…» открывает свои тайны тому, кто умеет смотреть и видеть, тому, кто сохранил в себе способность удивляться и воспринимать новое.

(Ответы на первые три задачи в следующем номере, над остальными поломайте голову сами.)

Комментарии к статье

* Все цитаты и рисунки Д. Тенниелла взяты из книги Кэрролл Л. Приключения Алисы в Стране чудес. Сквозь зеркало и что там увидела Алиса, или Алиса в Зазеркалье / Пер. с англ. Н. М. Демуровой. — 2-е изд. — М.: Наука, 1991

Математика в творчестве Льюиса Кэрролла: «Логический абсурд» Алисы в стране чудес

Лидия Астрецова 1 лет назад Просмотров:

1 # 07, июль 2016 УДК Математика в творчестве Льюиса Кэрролла: «Логический абсурд» Алисы в стране чудес Брешков С.С., студент Россия, , г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Техническая физика» Константинова И.А., студент Россия, , г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Техническая физика» Шарова Ю.С., студент Россия, , г. Москва, МГТУ им. Н.Э. Баумана, кафедра «Техническая физика» Научный руководитель: Губанов Н.Н., д.ф.н., доцент Россия, , г. Москва, МГТУ им. Н.Э Баумана, кафедра «Философия» Всемирно известный автор книг про удивительные приключения девочки Алисы Лутвидж Доджсон оставил после себя не только сказочные истории, но и серьезные математические труды. В 1858 г. он написал «Алгебраический разбор V книги Эвклида». Главным трудом древнегреческого математика Евклида являлось сочинение «Начало», состоящее из 13 книг. Его пятая книга, которую и рассматривал Лутвидж Доджсон в своей работе, была посвящена общей теории пропорций. В 1867 г. свет увидела книга «Элементарное руководство по теории детерминантов» элементарный трактат о детерминантах с их применением для линейных и алгебраических уравнений. В 1879 г. Доджсон завершил труд, посвященный древнегреческому математику, «Евклид и его современные соперники». В книге он защищал евклидов подход к преподаванию геометрии. Несмотря на то, что это научная работа, повествование в ней ведется в форме причудливых диалогов между математиком по имени Минос и профессором Никто, который воплощает в себе «современных соперников Эвклида». Цитата из предисловия к этой книге была нанесена на первый логотип «Википедии». В 1888 г. писатель издал первую часть «Математические курьезов», а

2 через пять лет, в 1893 г. вторую под названием «Полуночные задачи», в который вошли 72 задачи по тригонометрии, алгебре и планиметрии. В 1878 г. Доджсон выпустил сборник загадок и игр для детей «История с узелками» с забавными героями, в 1887 г. книгу «Логическая игра», в которой познакомил юных читателей с оригинальным графическим методом решения соритов и силлогизмов. Учебную тему продолжила «Символическая логика» (часть I опубликована в 1890 г.), также изобилующая примерами и головоломками, что выгодно отличало ее от сухих учебников современников. Вторая же часть «Символической логики» издана только почти столетие спустя: в 1977 г. А в 1865 г. в Англии вышла в свет книга о приключениях девочки Алисы в Стране чудес. Прочитав сказку, тогдашняя королева Англии Виктория пришла в восторг и тут же приказала купить для нее все сочинения автора сказки Кэрролла. Каково же было ее удивление и разочарование, когда оказалось, что это были труды по высшей математике! Под именем Льюиса Кэрролла скрывался все тот же Чарльз Лутвидж Доджсон, преподаватель математики и логики в Оксфордском Крайст-колледже. Написал он ее для дочерей декана, с которыми очень подружился, Лорины, Алисы и Эдит Лайделл. Что же до псевдонима, то Доджсон поступил очень просто: подверг свое полное имя двойной трансформации. Сначала перевел Charles Lutwidge на латинский язык, что дало Carolus Ludovicus, затем поменял местами и перевел Ludovicus Carolus обратно на английский. Получилось «Льюис Кэрролл» С той поры прошло полтора столетия, а книжки про Алису, написанные для детей, продолжают будоражить умы взрослых. Спрашивается, почему? Потому что, по словам американского математика Норберта Винера, «невозможно доказательство того, что природа подчинена законам, ибо все мы знаем, что мир со следующего момента может уподобиться игре в крокет из книги Алиса в стране чудес». По этой же причине выдающийся английский философ Бертран Рассел, чей вклад в математическую логику считается едва ли не самым значительным и фундаментальным со времен Аристотеля, предлагал издавать сказки Льюиса Кэрролла с грифом «Только для взрослых» [9]. Кэрроллу (будем теперь называть Доджсона его псевдонимом), по мнению многих, удалось в своих детских книгах изложить ни больше ни меньше, как основы мироздания. Эпизод, когда в Стране чудес Алиса то увеличивается до огромных размеров, то уменьшается, наглядно иллюстрирует теорию расширения и сжатия Вселенной. Сны, в которых Алиса видит Черного Короля, а он, в свою очередь, видит во сне Алису, пример бесконечно убывающей математической последовательности. Сама же структура сказок, Молодежный научно-технический вестник ФС , ISSN

3 написанных полтора века назад, удивительно напоминает виртуальный мир современных компьютерных игр, которые, равно как и сами компьютеры, по сути, детище математики [5]. В сказках об Алисе есть масса аналогий, физико-математических загадок. Падение Алисы в кроличью нору происходит с равномерно возрастающим ускорением. (Позднее Альберт Эйнштейн провел «мысленный эксперимент», в котором описывал падение воображаемого лифта для объяснения теории относительности) [6]. В Зазеркалье Черная Королева говорит девочке: «Ну а здесь, знаешь ли, приходится бежать со всех ног, чтобы только остаться на том же месте! Если же хочешь попасть в другое место, тогда нужно бежать, по меньшей мере, вдвое быстрее!» это еще один пример иллюстрации теории относительности [8]. Оказавшись в конце XIX в. в Зазеркалье, «где все наоборот», Алиса полагает, что ей ни в коем случае нельзя пить здешнее молоко. А спустя 68 лет, в 1957 г., американским физикам была присуждена Нобелевская премия за работу по теории антивещества, которая утверждает, что при взаимодействии материи с антиматерией непременно произойдет взрыв [13]. Научным «шифром», похоже, являются даже стихи из «Алисы в Зазеркалье»: английский астроном Артур С. Эддингтон утверждал, что их фонетическая структура строится на тех же принципах, что и математическая теория групп, открытая лишь в ХХ столетии. Когда «Алиса в стране чудес» была только опубликована, многие почти сразу подметили, что ее персонажи списаны с реальных людей: уже упомянутая выше Алиса это Алиса Плезенс Лайдел, дочь оксфордского декана, Лори и Орленок ее сестры Лорина и Эдит; сам Доджсон, который был заикой, это Додо и так далее. А математики обратили внимание на научный полемический тон сугубо детской, на первый взгляд, книги. В середине XIX в. математика быстро превратилась в то, чем она является сегодня в отточенный язык для описания концептуальных отношений между вещами. Но Кэрролл полагал, что ей по-прежнему не хватает логики, интеллектуальной строгости. Для подтверждения своей правоты он воспользовался «евклидовым методом» доказательством от противного, то есть проверкой актуальности той или иной идеи путем доведения предположений до логического предела, на первый взгляд кажущегося абсурдным, но на деле исполненного глубокого системного смысла. «Скажите, пожалуйста, куда мне отсюда идти? Это во многом зависит от того, куда ты хочешь прийти, ответил Кот. Да мне почти все равно, начала Алиса.

4 Тогда все равно, куда идти, сказал Кот. Лишь бы попасть куда-нибудь, пояснила Алиса. Не беспокойся, куда-нибудь ты обязательно попадешь, сказал Кот, конечно, если не остановишься на полпути» [1]. Уже беседа Алисы с Гусеницей в самом начале повествования это пародия на труды по математической логике и системе рядов Огастеса де Моргана [9], шотландского математика и логика, тогдашнего президента Лондонского математического общества, который утверждал, что любая процедура действительна, пока она следует собственной внутренней логике. Этот подход позволял, к примеру, даже извлекать квадратный корень из отрицательного числа, что и сам Де Морган называл «непонятным и нелепым». Рассуждения Де Моргана о том, что алгебра это, по сути, «восстановление и сокращение», выводили привередливого логика Доджсона из себя. «Он не только учил детей стоять на голове, писал о Кэрролле английский христианский мыслитель Гилберт Честертон. Он учил ученых стоять на голове. Но какая же это была голова, если на ней можно было так стоять!» [10]. Главная особенность абсурда Кэрролла состоит в том, что в нем, если разобраться, всегда присутствует строгая, почти математическая система. Уже в начале повествования, когда Алиса встречается с Синей Гусеницей, восседающей на огромном, ростом с девочку, грибе, между ними завязалась беседа. Девочка пожаловалась на свой маленький рост. «Мне бы хотелось хоть капельку подрасти. Три дюйма такой ужасный рост! Со временем привыкнешь, возразила Гусеница. Потом она сползла с гриба и скрылась в траве, бросив Алисе на прощанье: Откусишь с одной стороны подрастёшь, с другой уменьшишься! С одной стороны чего? подумала Алиса. С другой стороны чего? Гриба, ответила Гусеница и исчезла из виду. С минуту Алиса задумчиво смотрела на гриб, пытаясь определить, где у него одна сторона, а где другая; гриб был круглый, и это совсем сбило её с толку» [10]. В ответах Синей Гусеницы, безусловно, присутствовала своя логика. Но, следуя другой математической логике, объективные свойства окружности таковы, что у круглого гриба вообще не может быть сторон. Руководствуясь логикой универсальной арифметики, где размер может варьироваться между девятью футами и тремя дюймами, Льюис Кэрролл соединяет несоединимое и с такой же легкостью разъединяет неразрывное. «Прощайте, ноги!», говорит Алиса стремительно убегающим от нее ногам. И принимается строить планы, как она будет посылать им подарки к Рождеству. Потом Алиса съеда- Молодежный научно-технический вестник ФС , ISSN

5 ет еще немного гриба, и ее шея вытягивается, как у змеи, раздражая голубей. Наконец, ей удается методом проб и ошибок найти способ уменьшить себя до девяти дюймов. Не обошел вниманием Кэрролл и еще одну математическую «новацию» того времени геометрию размещения и ее принцип последовательности, построенный на идее, что одна фигура может быть согнута или растянута в другую, если она сохраняет свои основные свойства. Идея эта впоследствии нашла свое развитие в топологии законах связности, взаимного положения и следования точек, линий, поверхностей, тел и их частей или их совокупности в пространстве, независимо от отношений мер и величин [4]. В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов: кружка и бублик с точки зрения топологии неотличимы [7]. Но Кэрролл обратил внимание на то, что руководствуясь принципом «непрерывной трансформации» объекта, можно все довести до абсурда: Алиса берет на руки ребенка Герцогини, но он тут же превращается в свинью и убегает в лес. Чеширский Кот говорит на это: «Я так и думал». Он вообще говорит голосом традиционной геометрической логики. «Скажи, куда ты хочешь идти, если хочешь знать, как туда добраться», отвечает он на вопрос Алисы, где искать сбежавшую свинью, а затем медленно и частями исчезает. В итоге от Кота остается лишь одна улыбка. Привлекательная гармония чистой науки, по мнению Кэррола, управляет хаосом, как Чеширский Кот своей зримостью. Растворяясь по собственной надобности, кот оставляет вместо себя один лишь чистый знак у Чеширского Кота это беззубая и безгубая улыбка. «Улыбка без кота» одна из загадок на убывание, предложенных автором, представляет собой фактическое описание чистой математики: математические теоремы часто могут быть успешно приложены к описанию внешнего мира, но сами по себе теоремы чистая абстракции. В абсурде Кэрролла всегда присутствует строгая, почти математическая система. «Едят ли кошки мошек? Едят ли мошки кошек?» твердит сонная Алиса, меняя действующих лиц местами, но вскоре отбрасывает эти мысли. Какая ей разница? Философы и логики видят в этом эпизоде отсылку к школе логического эмпиризма. «Вот судья», размышляет Алиса в сцене суда, переворачивая причину и следствие. «Раз в парике, значит судья». Дрожащий от страха Шляпник откусывает вместо бутерброда кусок чашки, которую держит в другой руке. «Задом наперед, совсем наоборот», как сказал бы по этому поводу Траляля. Принцип этот подчеркивают наставления, которые дают Алисе участники Безумного Чаепития. «Я говорю, что думаю, заявляет Алиса, и думаю, что говорю». «Это совсем не одно и то же, поправляют они ее. Ведь не все равно, как сказать: «Я вижу то, что ем», или «Я ем то, что вижу», а Соня добавляет: «Так ты еще скажешь, будто «Я дышу, когда сплю», и «Я сплю, когда дышу», одно и то же!» [1].

6 Кэрролл разрывает даже привычные сочетания слов рычагом формальной логики. «Когда тебе дурно, всегда ешь занозы, советует Алисе Король. Лучше средства не сыщешь!» Алиса удивлена. «Можно брызнуть холодной водой иди дать понюхать нашатырю. Это гораздо приятнее, чем занозы!» говорит она. «Знаю, знаю, отвечает Король. Но я сказал: «Лучше средства не придумаешь!» Лучше, а не приятнее» [1]. Очень интересна роль, которую Кэрролл отвел двум персонажам Шляпнику и Мартовскому Зайцу, которых «чистая математика» в лице Черширского Кота считает не иначе как «сумасшедшими». Оба они, в принципе, защищают позицию математика Уильяма Роуэна Гамильтона одного из новаторов алгебры, идеи которого Кэрролл горячо поддерживал. Гамильтон сформулировал перспективную задачу: если есть геометрия как наука о пустом пространстве, то по аналогии можно представить и некую науку о «чистом времени» [9]. Более того, он предположил, что алгебра это и есть такая наука, просто люди не улавливают в ней скрытую временную специфику и не понимают, как на самом деле в алгебраических уравнениях воплощаются внутренние свойства времени. Гамильтон утверждал, что операции с числами вроде сложения или вычитания следует рассматривать как мерило того, что он называл «чистым временем». Эта идея буквально пленила Кэрролла и нашла свое отражение в главе «A Mad Tea-Party», название которое следовало бы переводить не как «Безумное чаепитие» (tea-party), а как «Безумное времяпитие» (tparty), где t математический символ времени. Автор заставил Шляпника, Зайца и Соню ходить вокруг чайного столика, чтобы отобразить, каким образом Гамильтон применял то, что он называл «кватернионами» числовую систему, основанную на четырех терминах. В 1860-е гг. кватернионы были провозглашены последним большим шагом в расчете движения, и Кэрролл считал их гениальным инструментом для опытных математиков, хотя и изобразил в виде раздражающей путаницы для таких, как Алиса (и, возможно, для многих других учеников). В безумном чаепитии время является отсутствующим четвертым элементом. Шляпник рассказывает Алисе, что он поссорился со временем в марте прошлого года, и сейчас «время для меня палец о палец не ударит». Таким образом, Шляпник, Заяц и Соня вынуждены вечно вращаться вокруг столика. Когда Алиса «выбывает» из чаепития, они пытаются засунуть Соню в чайник, чтобы существовать как независимые пары чисел сложные и сумасшедшие, как и раньше, но, по крайней мере, свободные покинуть это место. Алиса же идет навстречу Красной Королеве «слепой и бесцельной ярости», которая воплощает в данном случае иррациональное число. Но только ли «новая математика» волновала автора? Вовсе нет. Молодежный научно-технический вестник ФС , ISSN

7 К примеру, в эпизоде, когда Алиса пытается вспомнить таблицу умножения, она доходит до абсурда, все перепутав: «Значит, так: четырежды пять двенадцать, четырежды шесть тринадцать, четырежды семь. Так я до двадцати никогда не дойду!» Казалось бы, абсурд. И действительно: таблица Пифагора заканчивается на числе 12, а если следовать заданной прогрессии 4 5 = 12, 4 6 = 13, 4 7 = 14, то 4 12 = 19. До 20 не хватит единицы. Если мы примем 4 5 = 12 за аксиому, это значит, что мы считаем в системе исчисления с основанием 18. А в системе исчисления с основанием 21 действительно 4 6 = 13. Продолжив эту прогрессию (увеличивая основание в каждом шаге на 3), мы увидим, что произведения действительно увеличиваются каждый раз на один. Но метод перестанет работать, как только мы дойдем до 20: ведь 4 13 для системы с основанием 21 не равно 20. Выходит, с какой стороны ни посмотри, Алиса права: так она до 20 никогда не доберется. В главе «История Рыбного Деликатеса» Алиса получает урок классической философии наоборот. Ей снится известный школьный парадокс о неуязвимом Ахиллесе и черепахе. Ахиллес бегает быстрее черепахи, но черепаха, тем не менее, всегда впереди, так как всегда ближе к точке старта [3]. Алиса появляется как «третий» свидетель, которому два существа, классически медленное и классически быстрое, дают урок: «Тише едешь дальше будешь». Кэрролл дополняет его собственным выводом бег «от» и «к» приводит к убыванию времени. Аргентинский писатель Хорхе Луис Борхес назвал это открытие Кэрролла «бесконечным рядом убывающих расстояний». Работая над сказками об Алисе, Кэрролл-математик, безусловно, не забывал о том, что читать его книги будут не только коллеги по математическому «цеху», но и дети. Поэтому в них есть множество загадок, на которые автор не дает прямого ответа, оставляя читателям возможность найти их самим. Порой приоткрыть завесу тайны лучше, чем выдать все секреты и поделиться уже готовым знанием. Вот лишь один из подобных примеров: «В огромную лужу слез, которую наплакала Алиса, попáдали разные птицы и звери. Выбравшись из лужи, они стали искать способ, как побыстрее обсохнуть. По предложению Птицы Додо было решено устроить бег по кругу. «Сначала он нарисовал на земле круг. Правда, круг вышел не очень-то ровным, но Додо сказал: Правильность формы несущественна! А потом расставил всех без всякого порядка по кругу. Никто не подавал команды все побежали, когда захотели Через полчаса, когда все набегались и просохли, Додо вдруг закричал:

8 Бег закончен! Все столпились вокруг него и, тяжело дыша, стали спрашивать: Кто же победил? На этот вопрос Додо не мог ответить, не подумав как следует Наконец, Додо произнес: Победили все! И каждый получит награды!» [14]. Математиков в этой истории заинтересуют три момента. Во-первых, почему Додо расставил всех по кругу без всякого порядка? Почему для точек круга, а вернее окружности, невозможно указать, какая из трех произвольно взятых точек находится между двумя другими (по аналогии с точками прямой)? Что именно заставило Додо как следует задуматься в конце забега? Иначе говоря, почему в беге по кругу не оказалось проигравших, а были одни победители? И, наконец, что имел в виду Додо, сказав о нарисованной на земле линии: «Правильность формы несущественна»? А сколько в книге примеров зеркального изменения последовательности расположения точек на прямой или событий во времени! Как Алиса повстречалась с Черной Королевой? Для того чтобы приблизиться к ней, девочке пришлось идти. в противоположном направлении. «Вон она идет! закричал молоденький Шпорник. Алиса радостно оглянулась и увидела Чёрную Королеву. Пойду-ка я к ней навстречу, сказала Алиса. Навстречу? переспросила Роза. Так ты ее никогда не встретишь! Я бы тебе посоветовала идти в обратную сторону! Какая чепуха! подумала Алиса. Впрочем, вслух она ничего не сказала и направилась прямо к Королеве. К своему удивлению, она тут же потеряла ее из виду и снова оказалась у порога дома. В сердцах она отступила назад, огляделась по сторонам в поисках Королевы, которую наконец увидала вдали, и подумала: не пойти ли на этот раз в противоположном направлении? Всё вышло как нельзя лучше. Не прошло и минуты, как она столкнулась с Королевой у подножья холма, куда раньше никак не могла подойти». «Угости нас пирогом, сказал Алисе Лев в Зазеркалье. Алиса, поставив большое блюдо себе на колени, прилежно водила ножом. Ничего не понимаю! сказала она Льву. Я уже отрезала несколько кусков, а они опять срастаются! Молодежный научно-технический вестник ФС , ISSN

9 Ты не умеешь обращаться с Зазеркальными пирогами, заметил Единорог. Сначала раздай всем пирога, а потом разрежь его! Конечно, это было бессмысленно, но Алиса послушно встала, обнесла всех пирогом, и он тут же разделился на три части. А теперь разрежь его, сказал Лев, когда Алиса села на своё место с пустым блюдом в руках» [10]. Для жителей Зазеркалья было совершенно естественно, что утолить жажду можно, съев несколько сухариков; что за одно яйцо следует заплатить пять пенсов, а за два всего два. Чтобы перестала идти кровь из пальца, его надо уколоть булавкой, а чтобы остаться на том же месте, нужно бежать со всех ног. Белая Королева рассказывала Алисе, что в Зазеркалье «завтра никогда не бывает сегодня», а лучше всего обитателям Зазеркалья помнится то, что случится через некоторое время. Мало того, что Кэрролл оказался самым замечательным выдумщиком на свете он сумел соединить мир абсурдной, нелепой фантазии с тонкой и изысканной математической логикой. Он сломал существовавшие до него традиционно скучные, серые и утомительные представления о математике как науке для «яйцеголовых» мужей. Он убедил всех в том, что, если идти в глубь нелепого, можно дойти до смысла. И наоборот (в этом открытие Льюиса Кэрролла, который просто думал на один ход дальше): если идти честно в глубь смысла, обязательно дойдешь до бессмыслицы, хаоса. Потому что эти вещи зеркальны. Поэтому «Алису» так любят и математики, и физики, и философы, которые считают, что книги Кэрролла предвестники постструктурализма и постмодернизма, наравне с трудами Фридриха Ницше [2]. Здесь можно найти и отдельные идеи будущей синергетики, ставшей популярным междисциплинарным направлением познания в ХХ в. [12], и альтернативного исторического моделирования прошлого [11]. Аллегории Кэрролла уже давно получили и политическое, и психологическое, и богословское, и логическое толкования. И самое главное герои сказок об Алисе, что бы ни имел в виду Кэрролл, когда их писал, получили свое независимое существование. И живут вместе с нами полтора столетия. Список литературы [1]. Алиса в Стране Чудес / Перевод Д. Селиверстовой. М.: Эксмо, с. [2]. Губанов Н.И. Нищета философии постмодернизма // Философия и общество (45). С [3]. Губанов Н.И. Является ли философия наукой? // Философия и общество С