Содержанием исследования операций с теоретической точки зрения является

. особенную важность имеет

задача, общая для всей практики:

как располагать средствами своими

для достижения по возможности

Термин «операционные исследования», по-видимому, впервые применил в 1938 г. А.Раув, руководитель научной группы в Бодси (Англия), отнеся его к работам по оценке эффективности операций, проводимых военно-воздушными силами. Однако сегодня больше используют американский термин «исследование операций», имеющий тот же смысл.

Возникнув в недрах военных ведомств, новая наука, развиваясь, находит применение в самых разных областях человеческой деятельности, в том числе в бизнесе. Новые потребности общества стимулировали поиск новых подходов. Эту мысль хорошо выразил один из руководителей американской корпорации RCA Дж.Чейн: «Для того чтобы. эффективно действовать. управлять внутренними и внешними взаимодействиями. принимать своевременные и разумные решения, бизнес сейчас не может больше полагаться на традиционные методы и сбор информации; рамки успеха становятся слишком узкими, затраты слишком высокими, риск слишком большим, время слишком недостаточным, а конкуренция слишком сильной для того, чтобы действовать на основе предчувствия, интуиции или прошлой истории» 1 .

В настоящее время исследование операций можно рассматривать как одну из важнейших дисциплин, связанных с принятием решений, или как составную часть системного анализа. Несмотря на длительный период развития суть исследования операций остается неизменной: всесторонний анализ операции, оценка последствий возможных решений, поиск наиболее эффективных вариантов достижения цели. Не обсуждая различные точки зрения на исследование операций, приведем здесь только одно краткое, но, на наш взгляд, емкое определение, отражающее его главное предназначение.

Исследование операций (ИСО) — это наука о количественном

обосновании оптимальных решений.

При этом под оптимальным понимается решение, наилучшее в определенном смысле. Нельзя говорить об оптимальном решении вообще, корректное применение этого понятия требует конкретизации его смысла и условий, в которых принимается решение.

В то же время «операция» — весьма широкое понятие: это есть совокупность действий или мероприятий, направленных на достижение определенной цели. В ИСО описание операции включает следующее.

1. Цель операции, то есть то, ради чего проводится операция.

2. Оперирующая сторона — лицо или группа лиц, преследующих поставленную цель. В сложных операциях оперирующая сторона состоит из лица, принимающего решение (ЛПР), и аналитиков — специалистов по исследованию операций. Физически ЛПР — это одно лицо или группа лиц, наделенных правом принимать решения и несущих за них ответственность. Подготовка решений ложится на аналитиков. Разница между первыми и вторыми не только в знаниях методологии и методов ИСО, но и в информированности об операции, что весьма существенно. Причины этого кроются в сложности извлечения и представления информации, которой владеет ЛПР, или в нежелании ЛПР раскрывать все карты. В простых случаях ЛПР и аналитик могут быть в одном лице.

3. Активные средства — это, как правило, ресурсы, используемые для достижения цели.

4. Способы действий, поведения или использования активных средств. Их называют решениями, альтернативами или стратегиями в зависимости от типа операции.

5. Результаты или исходы операции.

6. Тип связи между решениями (стратегиями) и исходами операции. Он зависит от условий, в которых протекает операция.

Возьмем простой пример операции — подготовка к экзамену. Цель операции — успешная сдача экзамена. Оперирующая сторона: студент или студент (ЛПР) и методист (аналитик). Активные средства: время до экзамена, конспекты, учебные пособия и др. Существует много способов распорядиться перечисленными средствами, в том числе и написание шпаргалок. Так как у нас применяется четырехбалльная система оценки, то возможны четыре исхода сдачи экзамена. Всей операции присущи элементы случайности: самочувствие студента во время подготовки и сдачи экзамена, невозможность одинаково освоить все вопросы, настроение преподавателя, лотерейный способ выдачи экзаменационного билета и т.п. Поэтому между стратегиями подготовки к экзамену и его результатами связь неоднозначна.

Говоря об ИСО как о самостоятельном направлении, обычно отмечают его три основные особенности: системный подход, комплексный коллектив исследователей, применение научных методов. Под системным подходом понимается комплексная методология исследования сложных систем или проблем. В этой методологии определяющим является подход к любой части системы (проблемы) с позиции системы в целом, превалирование цели системы над целями ее подсистем. Как писал С. Янг, крупный специалист в области организации, «анализ отдельных свойств системы, конечно, важен, но он становится осмысленным только тогда, когда каждое свойство оценивается в контексте целостной системы» 2 . Другое важнейшее требование системного подхода состоит в том, что необходимо стремиться выявить все существенные факторы и взаимосвязи, влияющие на достижение цели системы. Для этого приходится расширять первоначальный объект исследования, искать скрытые от первого взгляда связи между факторами и частями системы.

Вторая особенность ИСО обусловлена необходимостью изучения и анализа проблемы с разных точек зрения, стремлением выйти за рамки стереотипов. Именно поэтому с момента возникновения исследования операций группы исследователей состояли из специалистов разного профиля (военных, математиков, физиков, психологов и др.), объединенных единой методологией. Такое комплексное исследование позволяет расширять множество альтернатив и находить действительно наилучшее решение.

Применение научных методов присуще любой науке, но в ИСО они имеют свою специфику, которая обусловлена задачей исследования и количественным характером результатов. Чтобы яснее представить эту особенность ИСО, рассмотрим, как проводится операционное исследование.

Исследование операций как научный подход к проблеме принятия управленческих решений

Исследование операций представляет собой применение научного метода к сложным проблемам, возникающим в управлении большими системами людей, машин, материалов и денег в промышленности, деловой сфере, государственном управлении, обороне и др. [1-4].

Корни исследования операций уходят в далекую историю. Резкое увеличение размеров производства, разделение труда в сфере производства обусловили постепенную дифференциацию и управленческого труда. Появилась необходимость в планировании материальных, трудовых и денежных ресурсов, в учете и анализе результатов труда и выработке прогноза на будущее. В управленческом аппарате начали выделяться подразделения: отдел финансов, сбыта, бухгалтерии и плановоэкономический отдел и др., принявшие на себя отдельные управленческие функции.

К этому периоду относятся первые работы по исследованию в области организации труда и управления — предвестники будущей науки.

Как самостоятельное научное направление, исследование операции оформилось в начале 40-х годов XX столетия. Первые публикации по исследованию операций относятся к 1939-1940 гг., в которых методы исследования операций применены для решения военных задач, в частности, для анализа и исследования боевых операций. Отсюда и возникло название дисциплины.

Основная задача исследования операций состоит в том, чтобы помочь менеджеру или иному лицу, принимающему решение, научно определить свою политику и действия среди возможных путей
достижения поставленных целей. Коротко исследование операций можно назвать научным подходом к проблеме принятия решений. Проблема — это разрыв между желаемым и фактически наблюдаемым состояниями (прежде всего целями) той или иной системы. Решение — это средство преодоления такого рода разрыва, выбор одного из многих объективно существующих курсов действий, который позволил бы перейти от наблюдаемого состояния к желаемому.

В настоящее время под операцией понимается система действий, объединенных общим замыслом (управляемое целенаправленное мероприятие), а под основной задачей исследования операций — разработка и исследование путей реализации этого замысла [5-8].

Ясно, что такое весьма широкое понимание операции охватывает значительную часть деятельности людей. Однако наука о принятии решений, о поиске путей достижения цели и особенно ее математическая составляющая еще весьма далеки от завершения даже по основным вопросам.

Совокупность людей, организующих операцию и участвующих в ее проведении, принято называть оперирующей стороной. Следует иметь в виду, что на ход операции могут оказывать влияние лица и природные силы, далеко не всегда содействующие достижению цели в данной операции.

Во всякой операции существует лицо (группа лиц), облеченное полнотой власти и наиболее информированное о целях и возможностях оперирующей стороны и называемое руководителем операции или лицом, принимающим решение (ЛПР). ЛПР несет полную ответственность за результаты проведения операции.

Особое место занимает лицо (группа лиц), владеющее математическими методами и использующее их для анализа операции. Это лицо (исследователь операции, исследователъ-аналитик) само решений не принимает, а лишь помогает в этом оперирующей стороне. Степень его информированности определяется ЛПР. Так как исследователь-аналитик, с одной стороны, не имеет об операции всей информации, которой обладает ЛПР, а с другой, — как правило, более осведомлен в общих вопросах методологии принятия решений, то желательно, чтобы взаимоотношения между исследователем операции и оперирующей стороной имели характер творческого диалога. Результатом этого диалога должен быть выбор (или построение) математической модели операции, на основе которой формируется система объективных оценок конкурирующих способов действий, более четко обозначается окончательная цель операции и появляется понимание оптимальности выбора образа действий. Право оценки альтернативных курсов действий, выбора конкретного варианта проведения операции (принятие решения) принадлежит ЛПР. Это обусловлено еще и тем, что абсолютных критериев рационального выбора не существует — во всяком акте принятия решения неизбежно содержится элемент субъективизма. Единственный объективный критерий — время, — в конце концов, покажет, насколько разумным было принятое решение.

Для того чтобы пояснить, какое место занимает математическая составляющая в исследовании операций, опишем коротко основные этапы разрешения проблемы принятия решения.

2- й шаг — выбрать модель (рис. 2).

В случае, если проблема сформулирована корректно, появляется возможность выбора готовой модели (из банка моделей, описывающих стандартные ситуации), разработка которой поможет в разрешении рассматриваемой проблемы, либо, если готовой модели нет, возникает необходимость создания такой модели, которая в достаточной степени точно отражала бы существенные стороны данной проблемы.

Модели могут быть очень разными: есть физические (iconic) модели, аналоговые (analog). Мы будем говорить здесь в основном о математических моделях.

Существует много разнообразных математических моделей, которые достаточно хорошо описывают различные ситуации, требующие принятия тех или иных управленческих решений. Выделим из них следующие три класса — детерминированные, стохастические и игровые модели.

При разработке детерминированных моделей исходят из предпосылки, что основные факторы, характеризующие ситуацию, вполне определенны и известны. Здесь обычно ставится задача оптимизации некоторой величины (например, минимизация затрат).

Стохастические модели применяются в тех случаях, когда некоторые факторы носят неопределенный, случайный характер.

Наконец, при учете наличия противников либо союзников с собственными интересами необходимо применение теоретико-игровых моделей.

В детерминированных моделях обычно имеется некий критерий эффективности, который требуется оптимизировать за счет выбора управленческого решения. (Впрочем, следует иметь в виду, что почти всякая сложная практическая задача является многокритериальной.)

В стохастических и игровых моделях ситуация усложняется еще больше. Зачастую выбор самого критерия зависит здесь от конкретной ситуации и возможны различные критерии эффективности принимаемых решений.

При выборе и/или создании модели важно суметь найти верный баланс между точностью модели и ее простотой. Привлечение успешно действующих моделей приходит с опытом и практикой, в соотнесении конкретных ситуаций с математическим описанием наиболее существенных сторон рассматриваемого явления. Конечно, ни одна математическая модель не может охватить всех особенностей изучаемой проблемы.

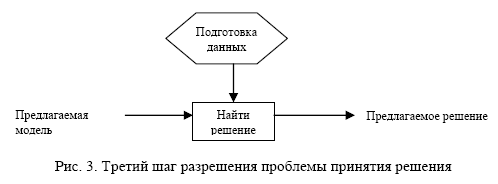
3- й шаг — найти решение (рис. 3).

Для поиска решения необходимы конкретные данные, сбор и подготовка которых требуют, как правило, значительных совокупных усилий. При этом стоит подчеркнуть, что даже в случае, если необходимые данные уже имеются, их часто приходится преобразовывать к виду, соответствующему выбранной модели.

4- й шаг — тестировать решение (рис. 4).

Полученное решение обязательно должно быть проверено на приемлемость при помощи соответствующих тестов. Неудовлетворительность решения обычно означает, что модель не точно отражает истинную природу изучаемой проблемы. В этом случае она должна быть либо как-то усовершенствована, либо заменена на другую, более подходящую модель.

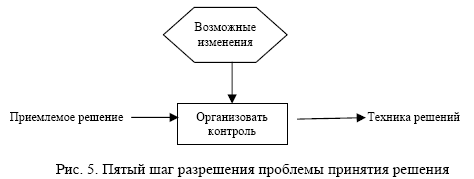
5- й шаг — организовать контроль (рис. 5).

Если найденное решение оказалось приемлемым, естественно, возникает необходимость создания механизма контроля за правильным использованием модели. Основная задача такого контроля состоит в обеспечении соблюдения ограничений, предполагаемых моделью, качества входных данных и получаемого решения. Полезно также иметь в виду, что найденное решение может быть использовано (и часто используется) не только для разрешения сиюминутной ситуации, но и при рассмотрении сходных обстоятельств в будущем. Заранее планируемая гибкость выбранной модели дает возможность использовать ее в течение более продолжительного промежутка времени.

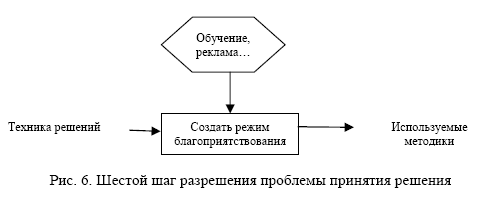
6- й шаг — создать режим благоприятствования (рис. 6).

Этот шаг часто оказывается самым трудным — внедрение новаций нередко наталкивается на незаинтересованность и даже на сопротивление. Поэтому обучение персонала, реклама, качество подготавливаемой документации и учет разнообразия поведенческих мотивов людей играют здесь решающую роль.

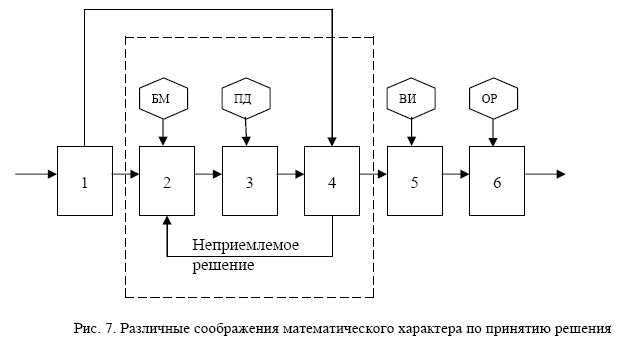
На схеме (рис. 7) пунктирной линией отмечена та часть процесса принятия решения, где заметную роль играют различные соображения математического характера.

Отметим, что сам термин «управление» можно понимать по-разному. Это и организация, в том числе и технологическая, той или иной осмысленной деятельности для достижения каких-либо целей (в качестве математического обеспечения здесь используются преимущественно детерминированные и стохастические модели), и изучение моделей поведения взаимодействующих сторон (здесь применяются игровые модели).

В настоящее время к решению сложных управленческих задач, представляющих практический интерес, привлекаются большие коллективы людей (и, добавим, значительные вычислительные средства) с разной профессиональной подготовкой и ориентацией, с разной степенью осведомленности о задаче в целом и, конечно, с разной степенью ответственности — от руководителя (ЛПР) до специа- листа-разработчика (исследователя) и рядового исполнителя.

Для того чтобы такое сложное образование могло достаточно плодотворно функционировать, важно подготовить тех, кто был бы способен к действенному связыванию разных его блоков, кто осуществлял бы нетривиальные коммуникационные функции, был посредником как между ЛПР и специалистом-разработчиком, так и между разработчиком и исполнителем. Этому посреднику вовсе не обязательно знать в деталях всю техническую сторону вопроса (это задача для найденных при его посредстве специалистов), а достаточно ориентироваться в основных идеях. Иными словами, если касаться только математической части, у него должны быть определенные представления о возможностях математических методов, об их идейных основаниях и о банке готовых математических моделей и ключевых методов.Одной из целей настоящего исследования является преодоление математической, методологической и языковой разобщенности исследователей сложной практической управленческой задачи. Только это дает возможность, с одной стороны, как можно точнее отразить в создаваемой (или выбираемой) модели реальные процессы, а с другой — создать (или выбрать) модель, простую настолько, чтобы можно было надеяться решить задачу до конца и получить обозримые и уже этим полезные результаты.

Накопленный опыт в решении практических задач исследования операций и его систематизация позволяют выделить по содержательной постановке следующие типичные классы задач [9-12]: 1) управление запасами; 2) распределение ресурсов; 3) ремонт и замена оборудования; 4) массовое обслуживание; 5) упорядочение; 6) сетевое планирование и управление; 7) выбор маршрута; 8) комбинированные .

Рассмотрим краткие особенности каждого класса задач.

Задачи управления запасами составляют самый распространенный и изученный в настоящее время класс задач исследования операций. Они обладают следующей особенностью. С увеличением запасов увеличиваются расходы на их хранение, но уменьшаются потери из-за возможной их нехватки. Следовательно, одна из задач управления запасами заключается в определении такого уровня запасов, который минимизирует следующий критерий: сумма ожидаемых затрат по хранению запасов, а также потерь из-за их дефицита.

Задачи распределения ресурсов возникают, когда существует определенный набор работ (операций), которые необходимо выполнять, а наличных ресурсов для выполнения каждой работы наилучшим образом не хватает.

Задачи ремонта и замены оборудования появляются в тех случаях, когда работающее оборудование изнашивается, устаревает и со временем подлежит замене.

Изношенное оборудование подвергают либо предупредительно-восстановительному ремонту, улучшающему его технологические характеристики, либо полной замене. При этом возможная постановка задачи такова. Определить сроки восстановительного ремонта и момент замены оборудования модернизированным, при которых суммарные ожидаемые затраты по ремонту и замене, а также потери вследствие ухудшения технологических характеристик — старения за все время эксплуатации оборудования — минимизируются.

Задачи массового обслуживания рассматривают вопросы образования и функционирования очередей, с которыми приходится сталкиваться в повседневной практике и в быту. Например, очереди самолетов, идущих на посадку, клиентов в ателье бытового обслуживания, абонентов, ожидающих вызов на междугородной телефонной станции и т.д.

Задачи упорядочения характеризуются следующими особенностями. Например, имеется множество различных деталей с определенными технологическими маршрутами, а также несколько единиц оборудования (фрезерный, токарный и строгальный станки), на которых эти детали обрабатываются. Так как одновременно обрабатывать более одной детали на одном станке невозможно, у некоторых из станков может образоваться очередь работ, т.е. деталей, ждущих обработки. Время обработки каждой детали известно, нужно определить такую очередность обработки деталей на каждом станке, при которой минимизируется некоторый критерий оптимальности, например, суммарная продолжительность завершения комплекса работ. Такая задача называется задачей календарного планирования или составления расписания, а выбор очередности запуска деталей в обработку — упорядочением.

Задачи сетевого планирования и управления (СПУ) рассматривают соотношение между сроком окончания крупного комплекса операций и моментами начала всех операций комплекса. Они актуальны при разработке сложных и дорогостоящих проектов.

Задачи выбора маршрута, или сетевые задачи, чаще всего встречаются при исследовании разнообразных процессов на транспорте и в системах связи. Типичной задачей является задача нахождения некоторого маршрута проезда из города А в город В при наличии нескольких маршрутов для разных промежуточных пунктов. Стоимость проезда и затрачиваемое на проезд время зависят от выбранного маршрута, необходимо определить наиболее экономичный маршрут по выбранному критерию оптимальности.

Комбинированные задачи включают в себя несколько типовых моделей задач одновременно. Например, при планировании и управлении производством приходится решать следующий комплекс задач:

— сколько изделий каждого типа необходимо выпустить и каковы оптимальные размеры партий изделий? (Типичная задача планирования производства);

— распределить производственные заказы по видам оборудования после того, как определен оптимальный план производства. (Типичная задача распределения);

— в какой последовательности и когда следует выполнять производственные заказы? (Типичная задача календарного планирования).

Так как эти три задачи нельзя решить изолированно, независимо друг от друга, то возможен следующий подход к решению данной комбинированной задачи. Сначала получают оптимальное решение задачи планирования производства. Затем, в зависимости от этого оптимума, находят наилучшее распределение оборудования. Наконец, на основе такого распределения составляют оптимальный график выполнения работ.

Однако такая последовательная оптимизация частных подзадач не всегда приводит к оптимальному решению задачи в целом. В частности, например, может оказаться, что нельзя произвести все изделия в оптимальных количествах из-за ограниченности имеющихся ресурсов. Пока еще не найден метод, позволяющий получить одновременный оптимум для всех трех задач, а возможно, он не существует для конкретных задач. Поэтому для решения подобных комбинированных задач применяется метод последовательных приближений, позволяющий подойти к искомому решению комбинированной задачи достаточно близко.

Предложенная классификация задач исследования операций не является окончательной. Со временем некоторые классы задач объединяются и становится возможным их совместное решение, стираются границы между указанными классами задач, а также появляются новые классы задач.

Следует также отметить, что ряд задач исследования операций не укладывается ни в один из известных классов и представляет наибольший интерес с научной точки зрения.

Основные особенности исследования операций

Общая цель математического программирования

Системный подход к анализу проблемы, непрерывность исследования, непрерывность и последовательность перехода от одной задачи к последующей, комплексность операционного исследования по разным направлениям с целью достижения оптимального решения

Основные этапы операционного исследования

Общая цель математического программирования

МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ И ОСНОВНЫЕ ПРИНЦИПЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ

ТЕМА 1

Важное значение для подготовки специалистов по автоматизации управления приобретают теоретические дисциплины, в которых изучаются научные основы управления производством и разрабатываются методы повышения эффективности управления экономическими системами.

Особое место среди этих дисциплин занимает исследование операций. Возникшая в начале 40-х годов XX в. в области задач управления боевыми операциями эта новая научная дисциплина быстро расширила свои исследования, охватив многие сферы целенаправленной человеческой деятельности, внесла в традиционные задачи управления производством новую методологию, известную под названием «системный подход».

Следует особо подчеркнуть связь между задачами повышения эффективности внедряемых АСУ й методологией исследования операций.

Целью исследования операций являются изучение и системный анализ систем организационного типа (организаций), отыскание в них оптимизационных задач управления, постановка и внедрение которых могут оправдать затраты на создание АСУ.

Важными этапами исследования операций являются:

— постановка оптимизационных задач,

— разработка математических моделей (формализация),

— нахождение оптимального решения и реализация его на практике.

При этом реализация полученных решений рассматривается как самостоятельная операционная задача.

Итак, исследование операций в отличие от чисто теоретических дисциплин имеет явно выраженную прикладную направленность.

Научно-техническая революция вызвала появление нового объекта исследований в области управления, получившего название большие, или сложные системы. Одним из самых значительных классов «больших систем» являются системы организационного управления. К ним относятся промышленные предприятия, производственные объединения, отрасли, экономика целого государства, а также глобальные системы (макросистемы), например группа государств.

Исследование операций представляет собой комплекс научных методов для решения задач эффективного управления организационными системами.

Исследование операций — это наука, занимающаяся разработкой и практическим применением методов наиболее эффективного (или оптимального) управления организационными системами.

Итак, предмет исследования операций — это системы организационного управления (организации), которые состоят из большого числа взаимодействующих между собой подразделений, причем интересы подразделений не всегда согласуются между собой и могут быть противоположными.

Целью исследования операций является количественное обоснование принимаемых решений по управлению организациями.

Решение, которое оказывается наиболее выгодным для всей организации, называется оптимальным, а решение, наиболее выгодное одному или нескольким подразделениям, будет субоптимальным.

В качестве примера типичной задачи организационного управления, где сталкиваются противоречивые интересы подразделений, рассмотрим задачу управления запасами предприятия.

Производственный отдел стремится выпускать как можно больше продукции при наименьших затратах. Поэтому он заинтересован в возможно более длительном и непрерывном производстве, т. е. в выпуске изделий большими партиями, ибо такое производство снижает затраты на переналадку оборудования, а следовательно и общие производственные затраты. Однако выпуск изделий большими партиями требует создания больших объемов запасов материалов, комплектующих изделий и т. д.

Отдел сбыта также заинтересован в больших запасах готовой продукции, чтобы удовлетворить любые запросы потребителя в любой момент времени. Заключая каждый контракт, отдел сбыта, стремясь продать как можно больше продукции, должен предлагать потребителю максимально широкую номенклатуру изделий. Вследствие этого между производственным отделом и отделом сбыта часто возникает конфликт по поводу номенклатуры изделий. При этом отдел сбыта настаивает на включении в план многих изделий, выпускаемых в небольших количествах даже тогда, когда они не приносят большой прибыли, а производственный отдел требует исключения таких изделий из номенклатуры продукции.

Финансовый отдел, стремясь минимизировать объем капитала, необходимого для функционирования предприятия, пытается уменьшить количество «связанных» оборотных средств. Поэтому он заинтересован в уменьшении запасов до минимума. Как видим, требования к размерам запасов у разных подразделений организации оказываются различными. Возникает вопрос, какая стратегия в отношении запасов будет наиболее благоприятной для всей организации. Это типичная задача организационного управления. Она связана с проблемой оптимизации функционирования системы в целом и затрагивает противоречивые интересы ее подразделений.

1. Характерной особенностью исследования операций является так называемый системный подход к анализу поставленной проблемы. Системный подход, или системный анализ, является основным методологическим принципом исследования операций, который состоит в следующем. Любая задача, какой бы частной она не казалась на первый взгляд, рассматривается с точки зрения ее влияния на критерий функционирования всей системы. Выше системный подход был проиллюстрирован на примере задачи управления запасами.

2. Для исследования операций характерно, что при решении каждой проблемы возникают все новые и новые задачи. Поэтому если сначала ставятся узкие, ограниченные цели, применение операционных методов не эффективно. Наибольший эффект может быть достигнут только при непрерывном исследовании, обеспечивающем преемственность в переходе от одной задачи к другой.

3. Одной из существенных особенностей исследования операций является стремление найти оптимальное решение поставленной задачи. Однако часто такое решение оказывается недостижимым из-за ограничений, накладываемых имеющимися в наличии ресурсами (денежные средства, машинное время) или уровнем современной науки. Например, для многих комбинаторных задач, в частности задач календарного планирования при числе станков п > 4, оптимальное решение при современном развитии математики оказывается возможным найти лишь простым перебором вариантов. Однако даже при небольших п число возможных вариантов оказывается настолько велико, что перебор всех вариантов при существующих ограничениях на быстродействие ЭВМ и допустимое машинное время практически не мыслим. Тогда приходится ограничиваться поиском «достаточно хорошего», или субоптимального решения. Поэтому исследование операций один из его создателей — Т. Саати — определил как «искусство давать плохие ответы на те практические вопросы, на которые даются еще худшие ответы другими методами» [1, 10].

4. Особенность операционных исследований состоит в том, что они проводятся комплексно, по многим направлениям. Для проведения такого исследования создается операционная группа. В ее состав входят специалисты разных областей знания: инженеры, математики, экономисты, социологи, психологи. Задачей создания подобных операционных групп является комплексное исследование всего множества факторов, влияющих на решение проблемы, и использование идей и методов различных наук.

Не нашли то, что искали? Воспользуйтесь поиском:

Методы исследования операций (стр. 1 из 5)

МЕТОДЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ

Программа дисциплины «Методы исследования операций» предназначена для студентов специальности «Экономическая кибернетика».

Цель учебной дисциплины «Методы исследования операций» — вооружить студентов фундаментальными теоретическими знаниями и помочь сформировать практические навыки в вопросах постановки и решения оптимизационных экономических задач методами исследования операций.

Дисциплина имеет практическую направленность относительно решения вопросов оптимального распределения ограниченных ресурсов, выбора оптимального варианта (объекта, проекта) из множества альтернативных вариантов и т.д.

Основное содержание дисциплины раскрывают такие темы:

1. Методы исследования операций и их использование в организационном управлении.

2. Общая задача линейного программирования и некоторые методы ее решения.

3. Теория двойственности и двойственные оценки в анализе решений линейных оптимизационных моделей.

4. Анализ линейных моделей экономических задач.

5. Транспортная задача. Постановка, методы решения.

6. Целочисленные задачи линейного программирования. Некоторые методы их решения и анализа.

II и III семестры

7. Элементы теории игр.

8. Блочное программирование.

9. Параметрическое программирование.

10. Задачи календарного планирования.

11. Задачи нелинейного программирования. Некоторые методы их решения.

12. Динамическое программирование.

13. Управление запасами.

Исследование операций — это наука, занимающаяся разработкой и практическим применением методов наиболее эффективного (или оптимального) управления организационными системами.

Предмет исследования операций — это системы организационного управления (организации), которые состоят из большого числа взаимодействующих между собой подразделений, причем интересы подразделений не всегда согласуются между собой и могут быть противоположными.

Основные особенности исследования операций.

1. Системный подход к анализу поставленной проблемы. Системный подход, или системный анализ, является основным методологическим принципом исследования операций, который состоит в следующем. Любая задача, какой бы частной она не казалась на первый взгляд, рассматривается с точки зрения ее влияния на критерий функционирования всей системы. Выше системный подход был проиллюстрирован на примере задачи управления запасами.

3. Одной из существенных особенностей исследования операций является стремление найти оптимальное решение поставленной задачи. Однако часто такое решение оказывается недостижимым из-за ограничений, накладываемых имеющимися в наличии ресурсами (денежные средства, машинное время) или уровнем современной науки. Например, для многих комбинаторных задач, в частности задач календарного планирования при числе станков п > 4, оптимальное решение при современном развитии математики оказывается возможным найти лишь простым перебором вариантов. Тогда приходится ограничиваться поиском «достаточно хорошего», или субоптимального решения. Поэтому исследование операций один из его создателей — Т. Саати — определил как «. искусство давать плохие ответы на те практические вопросы, на которые даются еще худшие ответы другими методами».

4. Особенность операционных исследований состоит в том, что они проводятся комплексно, по многим направлениям. Для проведения такого исследования создается операционная группа. В ее состав входят специалисты разных областей знания: инженеры, математики, экономисты, социологи, психологи. Задачей создания подобных операционных групп является комплексное исследование всего множества факторов, влияющих на решение проблемы, и использование идей и методов различных наук.

Каждое операционное исследование проходит последовательно следующие основные этапы:

1) постановка задачи,

2) построение математической модели,

3) нахождение решения,

4) проверка и корректировка модели,

5) реализация найденного решения на практике.

В самом общем случае математическая модель задачи имеет вид:

где Z=F(x, y) – целевая функция (показатель качества или эффективность) системы; х — вектор управляемых переменных; у — вектор неуправляемых переменных; Gi(x, y)— функция потребления i-го ресурса; bi — величина i-го ресурса (например, плановый фонд машинного времени группы токарных автоматов в станко-часах).

Определение 1. Любое решение системы ограничений задачи называется допустимым решением.

Определение 2. Допустимое решение, в котором целевая функция достигает своего максимума или минимума называется оптимальным решением задачи.

Для нахождения оптимального решения задачи (1.1)-(1.2) в зависимости от вида и структуры целевой функции и ограничений используют те или иные методы теории оптимальных решений (методы математического программирования).

1. Линейное программирование, если F(x, y),

2. Нелинейное программирование, если F(x, y) или

3. Динамическое программирование, если целевая функция F(x, y) имеет специальную структуру, являясь аддитивной или мультипликативной функцией от переменных х.

F(x)=F(x1, x2, …, xn) — аддитивная функция, если F(x1, x2, …, xn)=

4. Геометрическое программирование, если целевая функция F(x) и ограничения

Математическая модель задачи в этом случае записывается в виде

где I[0]=(m0, m0+1, …, n0); I[k]= (mk, mk+1, …, nk); mk+1=nk+1; m0=1; n0=n.

5. Стохастическое программирование, когда вектор неуправляемых переменных у случаен.

В этом случае математическая модель задачи (1.1—1.2) будет иметь

или вероятностных ограничениях

где My — математическое ожидание по у; Р — вероятность того, что выполняется условие gi (х)£ b.

6. Дискретное программирование, если на переменные xj наложено условие дискретности (например, целочисленности): xj — целое, j=1,2,…,n1£п.

7. Эвристическое программирование применяют для решения тех задач, в которых точный оптимум найти алгоритмическим путем невозможно из-за огромного числа вариантов. В таком случае отказываются от поиска оптимального решения и отыскивают достаточно хорошее (или удовлетворительное с точки зрения практики) решение. При этом пользуются специальными приемами — эвристиками, позволяющими существенно сократить число просматриваемых вариантов. Эвристические методы также применяют, когда оптимальное решение в принципе может быть найдено (т.е. задача алгоритмически разрешима), однако для этого требуются объемы ресурсов, значительно превышающие наличные.

Исследование операций в экономике

Предмет, цели, особенности и определения в исследовании операций. Сущность математического моделирования и этапы построения математических моделей. Основные теоремы линейного программирования. Оптимизационные задачи и методы нелинейного программирования.

Рубрика	Экономико-математическое моделирование
Вид	контрольная работа
Язык	русский
Дата добавления	30.05.2015
Размер файла	284,5 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

1. Общие понятия и определения в исследование операций

Следует усвоить основные понятия и определения исследования операций.

Операция — любое управляемое мероприятие, направленное на достижение цели. Результат операции зависит от способа ее проведения, организации, иначе — от выбора некоторых параметров. Всякий определенный выбор параметров называется решением. Оптимальными считают те решения, которые по тем или иным соображениям предпочтительнее других. Поэтому основной задачей исследования операций является предварительное количественное обоснование оптимальных решений.

Следует обратить внимание на постановку проблемы: само принятие решений выходит за рамки исследования операций и относится к компетенции ответственного лица или группы лиц, которые могут учитывать и другие соображения, отличные от математически обоснованных.

Если в одних задачах исследования операций оптимальным является решение, при котором выбранный критерий эффективности принимает максимальное или минимальное значение, то в других задачах это вовсе не обязательно. Так, в задаче оптимальным можно считать, например, такое количество торговых точек и персонала в них, при котором среднее время обслуживания покупателей не превысит, например, 5 мин, а длина очереди в среднем в любой момент окажется не более 3 человек (1, стр. 10-11).

Эффективность производственно-коммерческой деятельности в значительной степени определяется качеством решений, повседневно принимаемым менеджерами разного уровня. В связи с этим большое значение приобретают задачи совершенствования процессов принятия решений, решить которые позволяет исследование операций. Термин «исследование операций» впервые начал использоваться в 1939-1940 гг. в военной области. К этому времени военная техника и ее управление принципиально усложнилось вследствие научно-технической революции. И поэтому к началу Второй мировой войны возникла острая необходимость проведения научных исследований в области эффективного использования новой военной техники, количественной оценки и оптимизации принимаемых командованием решений. В послевоенный период успехи новой научной дисциплины были востребованы в мирных областях: в промышленности, предпринимательской и коммерческой деятельности, в государственных учреждениях, в учебных заведениях.

Исследование операций — это методология применения математических количественных методов для обоснования решений задач во всех областях целенаправленной человеческой деятельности. Методы и модели исследования операций позволяют получить решения, наилучшим образом отвечающие целям организации.

Основной постулат исследования операций состоит в следующем: оптимальным решением (управлением) является такой набор значений переменных, при котором достигается оптимальное (максимальное или минимальное) значение критерия эффективности (целевой функции) операции и соблюдаются заданные ограничения.

Предметом исследования операций являются задачи принятия оптимальных решений в системе с управлением на основе оценки эффективности ее функционирования. Характерными понятиями исследования операций являются: модель, изменяемые переменные, ограничения, целевая функция.

Предмет исследования операций в реальности — это системы организационного управления (организации), которые состоят из большого числа взаимодействующих между собой подразделений, причем интересы подразделений не всегда согласуются между собой и могут быть противоположными.

Основные особенности исследования операций:

Каждое операционное исследование проходит последовательно следующие основные этапы:

1) описание задачи планирования,

2) построение математической модели,

3) нахождение решения,

4) проверка и корректировка модели,

5) реализация найденного решения на практике.

Описание задачи планирования:

По своей содержательной постановке множество других типичных задач исследования операций может быть разбито на ряд классов:

· Задачи сетевого планирования и управления

рассматривают соотношения между сроками окончания крупного комплекса операций (работ) и моментами начала всех операций комплекса. Эти задачи состоят в нахождении минимальной продолжительности комплекса операций, оптимального соотношения величин стоимости и сроков их выполнения.

· Задачи массового обслуживания посвящены изучению и анализу систем обслуживания с очередями заявок или требований и состоят в определении показателей эффективности работы систем, их оптимальных характеристик, например в определении числа каналов обслуживания, времени обслуживания и т.п.

· Задачи управления запасами состоят в отыскании оптимальных значений уровня запасов (точек заказа) и размеров заказа. Особенность таких задач заключается в том, что с увеличением уровня запасов, с одной стороны, увеличиваются затраты на их хранение, но, с другой стороны, уменьшаются потери вследствие возможного дефицита запасаемого продукта.

· Задачи распределения ресурсов возникают при определенном наборе операций (работ), которые необходимо выполнять при ограниченных наличных ресурсах, и требуется найти оптимальные распределения ресурсов между операциями или состав операций.

· Задачи ремонта и замены оборудования актуальны в связи с износом и старением оборудования и необходимостью его замены с течением времени. Задачи сводятся к определению оптимальных сроков, числа профилактических ремонтов и проверок, а также моментов замены оборудования модернизированным.

· Задачи составления расписания (календарного планирования) состоят в определении оптимальной очередности выполнения операций (например, обработки деталей) на различных видах оборудования.

· Задачи планировки и размещения состоят в определении числа и места размещения новых объектов с учетом их взаимодействия с существующими объектами и между собой.

· Задачи выбора маршрута, или сетевые задачи, чаще всего встречаются при исследовании разнообразных задач на транспорте и в системе связи и состоят в определении наиболее экономичных маршрутов (1, стр.15).

Моделирование — процесс исследования реальной системы, включающий построение модели, изучение ее свойств и перенос полученных сведений на моделируемую систему.

Модель — это некоторый материальный или абстрактный объект, находящийся в определенном объективном соответствии с исследуемым объектом, несущий о нем определенную информацию и способный его замещать на определенных этапах познания.

Математическое моделирование — процесс установления соответствия реальному объекту некоторого набора символов и выражений, например математических. Математические модели наиболее удобны для исследования и количественного анализа, позволяют не только получить решение для конкретного случая, но и определить влияние параметров системы на результат решения.

В создание современного математического аппарата и развитие многих направлений исследования операций большой вклад внесли российские ученые Л. В. Канторович, Н. П. Бусленко, Е. С. Вентцель, Н. Н. Воробьев, Н. Н. Моисеев, Д. Б. Юдин и многие другие. Особо следует отметить роль академика Л. В. Канторовича, который в 1939 г., занявшись планированием работы агрегатов фанерной фабрики, решил несколько задач: о наилучшей загрузке оборудования, раскрое материалов с наименьшими потерями, о распределении грузов по нескольким видам транспорта и др. Л. В. Канторович сформулировал новый класс условно-экстремальных задач и предложил универсальный метод их решения, положив начало новому направлению прикладной математики — линейному программированию.

Значительный вклад в формирование и развитие исследования операций внесли зарубежные ученые Р. Акоф, Р. Беллман, Г. Данциг, Г. Кун, Дж. Нейман, Т. Саати, Р. Черч мен, А. Кофман и др. (1, стр. 17)

Этапы построения математических моделей:

Сущность построения математической модели состоит в том, что реальная система упрощается, схематизируется и описывается с помощью того или иного математического аппарата. Выделяют следующие основные этапы построения моделей.

1. Содержательное описание моделируемого объекта

Словесно описывается объект моделирования, цели его функционирования, среда, в которой он функционирует, выявляются отдельные элементы, возможные состояния, характеристики объекта и его элементов, определяются взаимосвязи между элементами, состояниями, характеристиками. Такое предварительное, приближенное представление объекта исследования называется концептуальной моделью. Этот этап является основой для последующего формального описания объекта.

2. Формализация операций

На основе содержательного описания определяется и анализируется исходное множество характеристик объекта, выделяются наиболее существенные из них. Затем выделяют управляемые и неуправляемые параметры, вводят символьные обозначения. Определяется система ограничений, строится целевая функция модели. Таким образом, происходит замена содержательного описания формальным (символьным, упорядоченным).

3. Проверка адекватности модели

Исходный вариант модели необходимо проверить по следующим аспектам:

1) все ли существенные параметры включены в модель?

2) нет ли в модели несущественных параметров?

3) правильно ли отражены связи между параметрами?

4) правильно ли определены ограничения на значения параметров?

Главным путем проверки адекватности модели исследуемому объекту выступает практика. После предварительной проверки приступают к реализации модели и проведению исследований. Полученные результаты моделирования подвергаются анализу на соответствие известным свойствам исследуемого объекта. По результатам проверки модели на адекватность принимается решение о возможности ее практического использования или о проведении корректировки.

4. Корректировка модели

На этом этапе уточняются имеющиеся сведения об объекте и все параметры построенной модели. Вносятся изменения в модель, и вновь выполняется оценка адекватности.

5. Оптимизация модели

Сущность оптимизации (улучшения) моделей состоит в их упрощении при заданном уровне адекватности. В основе оптимизации лежит возможность преобразования моделей из одной формы в другую. Основными показателями, по которым возможна оптимизация модели, являются время и затраты средств для проведения исследований и принятия решений с помощью модели.

В самом общем случае математическая модель задачи имеет вид:

где Z=F(x, y) — целевая функция (показатель качества или эффективность) системы; х — вектор управляемых переменных; у — вектор неуправляемых переменных; Gi(x, y)— функция потребления i-го ресурса; bi — величина i-го ресурса (например, плановый фонд машинного времени группы токарных автоматов в станко-часах).

Определение 1. Любое решение системы ограничений задачи называется допустимым решением.

Для нахождения оптимального решения задачи в зависимости от вида и структуры целевой функции и ограничений используют те или иные методы теории оптимальных решений (методы математического программирования).

1. Линейное программирование, если F(x, y), — линейны относительно переменных х.

2. Нелинейное программирование, если F(x, y) или — нелинейны относительно переменных х.

F(x)=F(x1, x2, …, xn) — аддитивная функция, если F(x1, x2, …, xn)=, и функция F(x1, x2, …, xn) — мультипликативная функция, если F(x1, x2, …, xn)=.

4. Геометрическое программирование, если целевая функция F(x) и ограничения представляют собой функции вида

Математическая модель задачи в этом случае записывается в виде

где I[0]=(m0, m0+1, …, n0); I[k]= (mk, mk+1, …, nk); mk+1=nk+1; m0=1; n0=n.

5. Стохастическое программирование, когда вектор неуправляемых переменных у случаен.

В этом случае математическая модель задачи (1.1—1.2) будет иметь

или вероятностных ограничениях

где My — математическое ожидание по у; Р — вероятность того, что выполняется условие gi (х)Ј b.

6. Дискретное программирование, если на переменные xj наложено условие дискретности (например, целочисленности): xj — целое, j=1,2,…,n1Јп.

Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций.

3. Линейное программирование

Несмотря на требование линейности целевой функции и ограничений, в рамки линейного программирования укладываются задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи, задачи теории расписаний и т. д.

Основные теоремы линейного программирования

В основе методов решения задач линейного программирования лежат следующие теоремы.

Основная теорема линейного программирования, устанавливающая место нахождения оптимальных решений.

Теорема 2.1. Если целевая функция принимает максимальное значение в некоторой точке допустимого множества R, то она принимает это значение в крайней точке R (вершине выпуклого многогранника). Если целевая функция принимает максимальное значение более, чем в одной крайней точке, то она принимает это же значение в любой их выпуклой комбинации.

Из теоремы 2.1 следует, что при отыскании оптимального решения достаточно просмотреть только крайние точки допустимого множества решений R.

Теорема 2.2. Каждое допустимое базисное решение соответствует крайней точке R.

Справедлива также следующая теорема, обратная к теореме 2.2. Теорема 2.3. Если — крайняя точка допустимого множества решений R, то соответствующее решение x0 — является допустимым базисным решением системы ограничений задачи линейного программирования.

Используя результаты теорем 2.1 и 2.2, можно сделать вывод, что для отыскания оптимального решения задачи линейного программирования достаточно перебрать лишь допустимые базисные решения. Этот вывод лежит в основе многих методов решения задач линейного программирования.

Определение оптимального ассортимента. Имеется р видов ресурсов в количествах а1, а2, . аi, . аp и q видов изделий. Задана матрица А=||aik||, где аik характеризует нормы расхода i-го ресурса на единицу k-го изделия (k = 1, 2, . q).

Эффективность выпуска единицы k-го изделия характеризуется показателем сi, удовлетворяющим условию линейности.

Определить план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности принимает наибольшее значение.

4. Нелинейное программирование

В данной главе описываются оптимизационные задачи нелинейного программирования (НЛП), математические модели которых содержат нелинейные зависимости от переменных. Источники нелинейности относятся в основном к одной из двух категорий:

1) реально существующие и эмпирически наблюдаемые нелинейные соотношения, например: непропорциональные зависимости между объемом производства и затратами; между количеством используемого в производстве компонента и некоторыми показателями качества готовой продукции; между затратами сырья и физическими параметрами (давление, температура и т.п.) соответствующего производственного процесса; между выручкой и объемом реализации и др.;

2) установленные (постулируемые) руководством правила поведения или задаваемые зависимости, например: формулы или правила расчета с потребителями энергии или других видов услуг; эвристические правила определения страховых уровней запаса продукции; гипотезы о характере вероятностного распределения рассматриваемых в модели случайных величин; различного рода договорные условия взаимодействия между партнерами по бизнесу и др.

Решать линейные задачи значительно проще, чем нелинейные, и если линейная модель обеспечивает адекватность реальным ситуациям, то ее и следует использовать. В практике экономического управления модели линейного программирования успешно применялись даже в условиях нелинейности. В одних случаях нелинейность была несущественной и ею можно было пренебречь, в других — производилась линеаризация нелинейных соотношений или применялись специальные приемы, например строились так называемые линейные аппроксимационные модели, благодаря чему достигалась требуемая адекватность. Тем не менее имеется большое число ситуаций, где нелинейность является существенной и ее нужно учитывать в явном виде.

Далее приводятся общая модель задачи нелинейного программирования и классы задач НЛП, а также описываются условия оптимальности решения.

Основные понятия НЛП:

* множество допустимых планов;

* модель нелинейного программирования;

* определять, является ли функция выпуклой;

* строить функцию Лагранжа задачи НЛП;

* проверять оптимальность полученных решений.

В общем виде задача НЛП описывается с помощью следующей модели нелинейного программирования:

исследование операция моделирование математический

где х = (x1, х2, . хn) — вектор переменных задачи.

Задача (1)—(3) называется задачей нелинейного программирования в стандартной форме на максимум.

Может быть сформулирована также задача НЛП на минимум.

Вектор х = (x1, х2, . хn), компоненты хj которого удовлетворяют ограничениям (2) и (3), называется допустимым решением или допустимым планом задачи НЛП.

Совокупность всех допустимых планов называется множеством допустимых планов.

Допустимое решение задачи НЛП, на котором целевая функция (1) достигает максимального значения, называется оптимальным решением задачи НЛП.

Возможное местонахождение максимального значения функции F(x) при наличии ограничений (2) и (3) определяется следующим общим принципом. Максимальное значение F(x), если оно существует, может достигаться в одной или более точках, которые могут принадлежать следующим множествам:

— внутренняя точка множества допустимых планов, в которой все первые частные производные

— точка границы множества допустимых планов>;

— точка множества допустимых планов, в которой функция F(x) недифференцируема>.

В отличие от задач линейного программирования, любая из которых может быть решена симплекс-методом, не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Какой-то алгоритм может оказаться чрезвычайно эффективным для решения задач одного типа и неудачным для задач другого типа.

Эффективность алгоритма может даже существенно зависеть от постановки задачи, например от изменения масштабов измерения тех или иных переменных. Поэтому алгоритмы разрабатываются для каждого класса (типа) задач. Программы, ориентированные на решение определенного класса задач, как правило, не гарантируют правильность решения любых задач данного класса, и оптимальность решения рекомендуется проверять в каждом конкретном случае.

В экономических приложениях рассматриваются следующие классы задач НЛП.

На рисунке приводится классификация задач и методов нелинейного программирования.

Рисунок. Классификация задач и методов нелинейного программирования

Большинство существующих методов в нелинейном программировании можно разделить на два больших класса:

1. Прямые методы — методы непосредственного решения исходной задачи. Прямые методы порождают последовательность точек — решений, удовлетворяющих ограничениям, обеспечивающим монотонное убывание целевой функции.

2. Недостаток: трудно получить свойство глобальной сходимости.

3. Задачи с ограничениями в виде равенств.

4. Метод замены переменных (МЗП)

5. Двойственные методы — методы, использующие понятие двойственности. В этом случае легко получить глобальную сходимость.

6. Недостаток: не дают решения исходной задачи в ходе решения — оно реализуемо лишь в конце итерационного процесса.

o Метод множителей Лагранжа (ММЛ)

o Методы штрафов

o Метод множителей

o Методы линеаризации для задач условной оптимизации

o Алгоритм Франка-Вульфа

o Метод допустимых направлений Зойтендейка

o Метод условного градиента

o Метод проекции градиента

o Сепарабельное программирование.

o Квадратичное программирование

1. Оптимизация нелинейной функции с ограничениями на неотрицательность значений переменных:

где х = (х1, х2. хn) — вектор переменных задачи.

Пусть F(x) — дифференцируемая функция.

Необходимые условия того, что в точке х0 достигается максимум функции F(x):

Это означает, что:

Если F(x) вогнутая функция (для задачи минимизации — выпуклая), то эти условия являются также достаточными.

Функция F(x) с числовыми значениями, определенная на выпуклом множестве точек К, называется вогнутой, если для любой пары точек х1, х2 и для всех чисел l, 0 Ј l Ј 1, выполняется неравенство

то функция F(x) называется выпуклой. Если имеют место строгие неравенства, то говорят, что функция строго вогнута или строго выпукла.

Данное определение вогнутости (выпуклости) годится для любого типа функции. Практически, однако, применять его трудно.

Для дважды дифференцируемой функции F(x) имеет место следующий критерий. Дифференцируемая функция F(x) строго вогнута в некоторой окрестности точки если выполняются следующие условия:

т.е. если знаки этих определителей чередуются указанным образом.

Здесь — частная производная второго порядка, вычисленная в точке х0.

Матрица размера п ґ п, составленная из элементов , называется матрицей Хессе (Hesse). По значениям ее главных миноров можно судить о выпуклости или вогнутости функции. Функция F(x) строго выпукла в малой окрестности точки х0, если все главные миноры ее матрицы Хессе строго положительны. Если имеют место нестрогие неравенства (і), то функция в окрестности точки х0 выпукла. Если при этом главные миноры матрицы Хессе от х не зависят, то функция всюду (строго) выпукла.

Весьма распространены относящиеся к данному типу модели квадратичного программирования, в которых целевая функция F(x) является квадратичной функцией переменных х1, х2, . хn. Существует большое число алгоритмов решения такого типа задач, в которых функция F(x) вогнутая (для задач минимизации — выпуклая).

2. Модели выпуклого программирования. К такого рода моделям относятся задачи НЛП (1)—(3), в которых F(x) — вогнутая (выпуклая) функция, a gi(x) — выпуклые функции. При данных условиях локальный максимум (минимум) является и глобальным.

Пусть F(x) и gi(x), i= 1. т, — дифференцируемые функции.

Необходимые и достаточные условия оптимальности решения — выполнение условий Куна — Таккера.

Рассмотрим задачу НЛП (1)—(3) и функцию Лагранжа

Условия Куна — Таккера оптимальности решения х0 для задачи максимизации F(x) имеют вид

где — частная производная функции Лагранжа по переменной хj при х = х0 и l = l0. Пусть максимальное значение F(x) равно F(x0) = F0. Числа связаны с F0 следующими соотношениями:

Из этих соотношений видно, что числа характеризуют реакцию значения F0 на изменение значения соответствующего bi. Например, если 0 , i=1. n.

Пусть wi — ставка заработной платы на предприятии i. Тогда доля дохода предприятия i в общей сумме прибыли объединения определится так:

Gi =ci*Pi-wi*Li , i=1,. . .,n.

Если величина фондов предприятия фиксирована, то объем продукции Pi однозначно определяется количеством рабочей силы .

Центр влияет на работу предприятий распределением дополнительного ресурса, который полностью находиться в его распоряжении. Если предприятие i получит дополнительный ресурс в количестве Vi, то оно сможет произвести продукцию в объеме

Задача центра состоит в распределении имеющегося в его распоряжении ресурса В, т. е. в определении оптимальных значений величин Vi, i =1. n, обеспечивающих максимум суммарной прибыли объединения в целом.

Математическая форма модели

В данной задаче считаем, что используется схема централизованного планирования, в рамках которой центр рассчитывает оптимальное распределение ресурсов, оптимальные величины рабочей силы при заданных параметрах модели. Конкретно центр изменяет Vi и Li, i = 1. n, из условий:

z = max (G1 + G2 + . + Gn) (6)

Vi, Vimin, Li 0,i=1. n (7)

Анализ чувствительности модели как способ восстановления финансового равновесия.

Основой сохранения и восстановления финансового равновесия предприятия и снижения уровня риска является анализ чувствительности предложенной модели. Анализ чувствительности состоит из следующих этапов:

1. Выбор ключевого показателя, т.е. такого параметра, относительно которого и рассчитывается чувствительность проекта (чаще всего это чистый приведенный доход и внутренняя норма доходности).

2. Выбор факторов, которые влияют на эти показатели.

3. Расчет значений ключевых показателей на разных этапах реализации проекта (поиск, проектирование, строительство, эксплуатация).

Чем выше чувствительность показателей к факторам внешней среды, тем более рискованным является проект. Для каждого показателя определяется чувствительность каждого момента времени или отрезка времени. Определяется эффективность проекта.

Часто во время анализа чувствительности определяется точка безубыточности проекта, т.е. определяется тот объем выпуска продукции, при котором предприятие выходит из зоны убытка.

Анализ чувствительности проекта разрешает специалистам учитывать риск и неопределенность. Например, если цена продукции оказалась критической, то возможно усилить программу маркетинга или снизить стоимость проекта. Если критическим окажется объем выпущенной продукции, то необходимо повысить квалификацию рабочих, уделить внимание обучению персонала, менеджерам и другим факторам повышения производительности.

Недостатки метода анализа чувствительности:

1. Метод не рассчитан на все случайное и возможное обстоятельства.

2. Метод не уточняет вероятность реализации альтернативных проектов.

Анализ чувствительности оптимального решения

Анализ чувствительности выполняется уже после получения оптимального решения задачи линейного программирования (ЛП). Его цель — определить, приведет ли изменение коэффициентов исходной задачи к изменению текущего оптимального решения, и если да, то, как эффективно найти новое оптимальное решение (если оно существует).

В общем случае изменение коэффициентов исходной задачи может привести к одной из следующих четырех ситуаций.

1. Текущее базисное решение остается неизменным.

2. Текущее решение становится недопустимым.

3. Текущее решение становится неоптимальным.

4. Текущее решение становится неоптимальным и недопустимым.

Во второй ситуации можно использовать двойственный симплекс-метод для восстановления допустимости решения. В третьей ситуации мы используем прямой симплекс-метод для получения нового оптимального решения. В четвертой для получения нового оптимального и допустимого решения следует воспользоваться как прямым, так и двойственным симплекс-методом.

1. «Исследование операций в экономике» учебное пособие для Вузов, 3-е издание, переработанное и дополненное, под ред. Н.Ш.Кремера, М.: Юрайт, 2013.

2. T.В. Алесинская « Основы логистики. Общие вопросы логистического управления» .Учебное пособие. Таганрог: Изд-во ТРТУ, 2005.

3. Афанасьев М.Ю., Суворов Б.П. Исследование операций в экономике: модели, задачи, решения. Учебное пособие, М, Инфра-М, 2003 г.

4. Филлипс Д., Гарсиа-Диас А. Методы анализа сетей. -М.: Мир,1984.

5. Грешилов А.А. Как принять наилучшее решение в реальных условиях. — М.: Радио и связь, 1991.

6. Попов Ю.Д. Линейное и нелинейное программирование. Учебное пособие. — Киев, 1988.

7. Зайченко Ю.П. Исследование операций. Учебное пособие для студентов вузов. — Киев: Вища школа. Головное издательство, 1979

8. Таха Х.. Введение в исследование операций: в 2-х книгах. — М.: Мир, 1985.

9. Акоф Р., Сасиени М. Основы исследования операций. — М.: Мир, 1997.

10. Акулич И.Л. Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986.

11. Данко. Высшая математика в примерах и задачах.

12. Алексеев В. М., Голеев В. М., Тихомиров В. М. Сборник задач по оптимизации: Теория, примеры, задачи. М., Наука, 1984.

13. Берман Г. Н. Сборник задач по курсу математического анализа. М., Наука, 1985.

14. Ильин В.А. Позняк Э.Г. Линейная алгебра. М., Наука, 1983.

15. Ильин В.А. Позняк Э.Г. Основы математического анализа. М., Наука, Ч.1,2, 1980.

16. Клетеник Д..В. Сборник задач по аналитической геометрии. М., Наука, 1984.

17. Кудрявцев Л.Д.. Курс математического анализа. М., Высш. шк., Т. 1-3, 1988.

18. Кудрявцев Л.Д.. Краткий курс математического анализа. М., Наука, 1989.

19. Кудрявцев Л.Д. Кутасов А..Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу. Предел. Непрерывность. Дифференцируемость. М., Наука, 1984.

20. Кремер Н. Ш., Путко Б. А. Тришин И.М., Фридман М. Ф. Высшая математика для экономистов. М., Банки и биржи, ЮНИТИ, 1998.

21. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. М., Высш. шк., 1999.

22. Ниворожкина Л.И., Морозова З.А. Основы статистики с элементами теории вероятностей для экономистов. Руководство для решения задач. Ростов н/Д., Феникс., 1999.

23. Данко П.Е. Высшая математика в упражнениях и задачах. Ч.2. М., Высш. шк., 1997.

24. Чистяков В.П. Курс теории вероятностей. М., Наука., 1987.

25. Севастьянов Б. А. Курс теории вероятностей и математической статистики. М., Наука., 1982.

26. Севастьянов Б.А., Чистяков В.П., Зубков А.М. Сборник задач по теории вероятностей. М., Наука., 1980.

27. Вентцель Е.С Исследование операций. Задачи. Принципы. Методология, 1980.

28. Горелик В.А., Ушаков И.А. Исследование операций. — М.: Машиностроение, 1986.

29. Исследование операций/ Под редакцией М.А. Войтенко и Н.Ш. Кремера.-М.: Экономическое образование, 1992.

30. Карасев А.И., Аксютин З.М., Савельева Т.И. Математические методы и модели в планировании М.: Экономика, 1987.

31. Исследование операций / Н. Н. Писарук. Минск : БГУ, 2013.272 c.

Размещено на Allbest.ru

Подобные документы

Графическое решение задач линейного программирования. Решение задач линейного программирования симплекс-методом. Возможности практического использования математического программирования и экономико-математических методов при решении экономических задач.

курсовая работа [105,5 K], добавлен 02.10.2014

Понятие и типы моделей. Этапы построения математической модели. Основы математического моделирования взаимосвязи экономических переменных. Определение параметров линейного однофакторного уравнения регрессии. Оптимизационные методы математики в экономике.

реферат [431,4 K], добавлен 11.02.2011

Изучение экономических приложений математических дисциплин для решения экономических задач: использование математических моделей в экономике и менеджменте. Примеры моделей линейного и динамического программирования как инструмента моделирования экономики.

курсовая работа [2,0 M], добавлен 21.12.2010

Основные понятия линейной алгебры и выпуклого анализа, применяемые в теории математического программирования. Характеристика графических методов решения задачи линейного программирования, сущность их геометрической интерпретации и основные этапы.

курсовая работа [609,5 K], добавлен 17.02.2010

Математическая формализация оптимизационной проблемы. Геометрическая интерпретация стандартной задачи линейного программирования, планирование товарооборота. Сущность и алгоритм симплекс-метода. Постановка транспортной задачи, последовательность решения.

учебное пособие [126,0 K], добавлен 07.10.2014

Теоретические основы экономико-математических методов. Этапы принятия решений. Классификация задач оптимизации. Задачи линейного, нелинейного, выпуклого, квадратичного, целочисленного, параметрического, динамического и стохастического программирования.

курсовая работа [2,3 M], добавлен 07.05.2013

Общая постановка задачи линейного программирования (ЛП). Приведение задачи ЛП к стандартной форме. Теоремы двойственности и их использование в задачах ЛП. Транспортная задача и её решение методом потенциалов. Интерполирование табличных функций.

курсовая работа [337,1 K], добавлен 31.03.2014

Цель работы: изучить и научиться применять на практике симплекс — метод для решения прямой и двойственной задачи линейного программирования. Математическая постановка задачи линейного программирования. Общий вид задачи линейного программирования.

реферат [193,4 K], добавлен 28.12.2008

Модель динамического программирования. Принцип оптимальности и уравнение Беллмана. Описание процесса моделирования и построения вычислительной схемы динамического программирования. Задача о минимизации затрат на строительство и эксплуатацию предприятий.

дипломная работа [845,3 K], добавлен 06.08.2013

Основные подходы к математическому моделированию систем, применение имитационных или эвристических моделей экономической системы. Использование графического метода решения задачи линейного программирования для оптимизации программы выпуска продукции.

курсовая работа [270,4 K], добавлен 15.12.2014

Работы в архивах красиво оформлены согласно требованиям ВУЗов и содержат рисунки, диаграммы, формулы и т.д.
PPT, PPTX и PDF-файлы представлены только в архивах.
Рекомендуем скачать работу.

Источники:

http://articlekz.com/article/5780
http://studopedia.ru/2_100166_osnovnie-osobennosti-issledovaniya-operatsiy.html
http://mirznanii.com/a/115463/metody-issledovaniya-operatsiy
http://revolution.allbest.ru/emodel/00562058_0.html