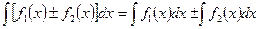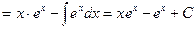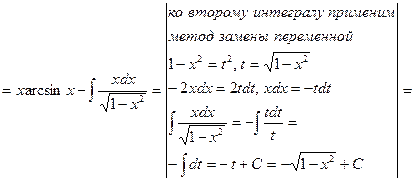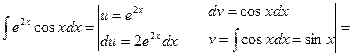Определение. Если существует конечный передел интегральной суммы (8)
при л>0, не зависящий от способа разбиения фn отрезка [a; b] на частичные отрезки и выбора промежуточных точек оk, то этот предел называют определенным интегралом (или интегралом Римана) от функции f(x) на отрезке [a; b] и обозначают:
Если указанный предел существует, то функция f(x) называется интегрируемой на отрезке [a; b] (или интегрируемой по Риману). При этом f(x)dx называется подынтегральным выражением, f(x) — подынтегральной функцией, х — переменной интегрирования, a и b — соответственно нижним и верхним пределами интегрирования.
Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения л стремится к нулю.
Геометрический смысл определенного интеграла. Пусть функция y=f(x) непрерывна на отрезке [a; b] и f(x) ? 0. Фигура, ограниченная графиком АВ функции y=f(x), прямыми x=a, x=b и осью Ох (рис. 1), называется криволинейной трапецией.
Интегральная сумма и ее слагаемые имеют простой геометрический смысл: произведение равно площади прямоугольника с основанием и высотой , а сумма представляет собой площадь заштрихованной ступенчатой фигуры (изображенной на рис. 1). Очевидно, что эта площадь зависит от разбиения фn отрезка [a; b] на частичные отрезки и выбора точек оk.
Чем меньше , k=1, n, тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Следовательно, за точную площадь S криволинейной трапеции принимается предел интегральной суммы при л>0:
Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.
Дата добавления: 2015-06-12 ; просмотров: 1238 ; Нарушение авторских прав
Определение. Неопределенным интегралом от функции на называется семейство первообразных, то есть выражение , где — одна из первообразных для функции на , — произвольная постоянная.
Для обозначения неопределенного интеграла вводится символ
, (5.3)
где знак называется интегралом, — подынтегральной функцией, — подынтегральным выражением, — переменной интегрирования.
Тогда согласно определению можно записать
. (5.4)
Определение. Операция нахождения неопределенного интеграла называется интегрированием функции .
Пример. Проверить правильность выполнения интегрирования
.
Решение. Дифференцируя результат интегрирования , получаем подынтегральную функцию.
Ответ. Интегрирование выполнено верно.
С геометрической точки зрения неопределенный интеграл представляет собой семейство непрерывных на и параллельных вдоль оси Oy кривых (рис. 5.1).
Свойства неопределенного интеграла
Свойство 1. Производная неопределенного интеграла равна подынтегральной функции, то есть
. (5.5)
Доказательство. С учетом (5.4) имеем
, что и требовалось доказать.
Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, то есть
. (5.6)
Доказательство. По определению дифференциала и учитывая (5.5), имеем
, что и требовалось доказать.
Свойство 3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, то есть
. (5.7)
Доказательство. Возьмем дифференциалы от обеих частей (5.7) с учетом свойства 2. Имеем
.
Равенство дифференциалов означает справедливость (5.7), что и требовалось доказать.
Замечание. Свойства 2 и 3 выражают взаимно обратный характер операций дифференцирования и интегрирования, что позволяет из формул и правил дифференцирования получить соответствующие формулы и правила интегрирования.
Свойство 4. Постоянный множитель можно выносить за знак интеграла, то есть
, (5.8)
где a — действительное число, отличное от нуля.
Доказательство. Возьмем производные от обеих частей (5.8) с учетом свойства 1. Имеем
.
Таким образом, функция и функция являются первообразными для одной и той же функции , что и означает справедливость (5.8).
Свойство 5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от каждой из функций, то есть
. (5.9)
Доказательство. Возьмем производные от обеих частей (5.9) с учетом свойства 1. Имеем
Таким образом, функция и функция являются первообразными для одной и той же функции , что и означает справедливость (5.9).
Учитывая взаимно обратный характер операций дифференцирования и интегрирования, можно записать интегралы от простейших функций, которые принято называть табличными. Будем полагать, что переменная интегрирования u есть некоторая функция , то есть .
Таблица основных интегралов
Часть формул этой таблицы непосредственно следует из определения операции интегрирования и таблицы производных. Справедливость остальных соотношений легко проверяется дифференцированием.
Определенный интеграл (стр. 1 из 5)
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
2. Геометрический смысл определенного интеграла
3. Основные свойства определенного интеграла
4. Формула Ньютона–Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям
Лекция 2. Применение определенных интегралов. несобственные интегралы
1. Площадь криволинейной трапеции
2. Объем тела вращения
3. Длина дуги плоской кривой
4. Несобственные интегралы с бесконечными пределами интегрирования
5. Несобственные интегралы от неограниченных функций
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
1) разобьем отрезок
2) в каждом из частичных отрезков
3) найдем произведения
4) составим сумму
которая называется интегральной суммой функции y = f ( x ) на отрезке [ а, b ]. С геометрической точки зрения интегральная сумма
5) найдем предел интегральной суммы, когда
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка
В этом случае функция
Теорема 1. Если функция
2. Геометрический смысл определенного интеграла
Пусть на отрезке
3. Основные свойства определенного интеграла
1. Значение определенного интеграла не зависит от обозначения переменной интегрирования:
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
4. Постоянный множитель можно выносить за знак определенного интеграла:
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
7. ( теорема о среднем ). Если функция
4. Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема 2. Если функция
которая называется формулой Ньютона–Лейбница. Разность
Таким образом, формулу (2) можно записать в виде:
Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную
Неопределенный интеграл представляет собой семейство функций
y = F(x) + C.
С геометрической точки зрения неопределенный интеграл представляет совокупность (семейство) кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т.е. вдоль оси Оу.
Возникает вопрос: для всякой ли функции f(x) существуют первообразные (а значит и неопределенный интеграл)?
На этот вопрос отвечает следующая
Теорема: Если функция f(x) непрерывна на отрезке [a,b], то для этой функции существуют первообразная (а значит и неопределенный интеграл).
Нахождение первообразной и отыскание неопределенного интеграла для функции f(x) называется интегрированием функции f(x).
Из определения неопределенного интеграла следуют следующие свойства:
1. Производная от неопределенного интеграла равна подинтегральной функции, т.е. (∫f(x)dx)’ = (F(x)+c)’=f(x)
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению d(∫f(x)dx) = f(x)dx
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная ∫dF(x) = F(x)+C.
4. Неопределенный интеграл от производной равен самой функции плюс произвольная постоянная С òF’(x)dx=F(x)+C.
5. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов (если каждый из них существует)
6. Постоянный множитель можно выносить за знак интеграла ∫аf(x)dx = а ∫f(x)dx.
7. Если ∫f(x)dx = F(x)+C, то
8. Если ∫f(x)dx = F(x)+C, то ∫f(x+b)dx = F(x+b)+C.
9. Если ∫f(x)dx = F(x)+C, то 
Непосредственно из определения интеграла и таблицы производных вытекает таблица интегралов.
Таблица интегралов.
1.  | 2.  |
3. 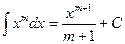 | 4.  |
5.  | 6.  |
7.  | 8.  |
9.  | 10.  |
11. 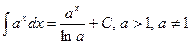 | 12.  |
13.  | 14.  |
15. 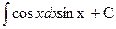 |
Рассмотрим примеры:
1. 
2.
3. 
4. 
Таблица интегралов записана для переменной интегрирования х, однако она также справедлива, если заменить х на другую переменную, которая может быть и некоторой функцией.
Например
5. 
6. 
Методы интегрирования
Интегрирование функций сводится к применению табличных интегралов. (Решить интеграл – значит свести его к табличному виду). Умение интегрировать состоит в том, чтобы с помощью свойств неопределенных интегралов преобразовать подинтегральное выражение к «табличному», или хотя бы сначала упростить. Для этого применяют различные методы интегрирования. Непосредственным методом мы уже прорешали несколько примеров. Один из наиболее применяемых методов – метод подстановки или метод замены переменной.
Метод замены переменной.
1. Метод замены переменной при нахождении неопределенного интеграла ∫f(x)dx состоит в применении формулы:
где х=φ(t) – дифференцируемая функция.
Формула (1) означает, что нахождение ∫f(x)dx сводится к нахождению другого интеграла, в котором подынтегральное выражение зависит от переменной t. Он получается заменой переменной по формуле х=φ(t). Однако общего правила выбора функции φ(t) нет.
При удачном выборе этой функции может оказаться, что новый интеграл проще и даже является табличным. В последнем случае выполняют интегрирование и находят первообразную как функцию переменной t. После замены этой переменной ее выражением через х получается искомый интеграл.
Покажем применение формулы (1) на примере:
Пример
7. 

Метод интегрирования по частям.
В дифференциальном исчислении была получена формула дифференциала произведения двух функций:
Проинтегрируем обе части
формула интегрирования по частям, где u=u(x), v=v(x) — функции, зависящие от х. Смысл формулы (2) состоит в том, чтобы в результате ее применения новый интеграл оказался табличным или хотя бы стал проще. Для применения формулы интегрирования по частям, подинтегральное выражение следует разбить на два множителя. Один из них обозначается u, а остальная часть обозначается через dv. Затем дифференцированием находится du, а интегрированием – функция v. При этом за u следует брать такую часть подинтегральной функции, которая при дифференцировании сильно не усложняется, а за dv – такую часть подинтегрального выражения, которая легко интегрируется.
Пример:
8.
Иногда этот метод приходится применять несколько раз, дополняя другие способы интегрирования.
9.
= -x 2 cosx + 2xsinx — 2òsinxdx = -x 2 cosx + 2xsinx + 2cosx + C;
10.

11.

Решим полученное уравнение относительно интеграла



Метод интегрирования по частям применяется при нахождении неопределенных интегралов вида:
1. ∫P(x) e αx dx, ∫P(x)sinmxdx, ∫P(x)cosmxdx
2. ∫P(x)lnxdx, ∫P(x)arcsinxdx, ∫P(x)arccosxdx, ∫P(x)arctgxdx, ∫P(x)arcctgxdx,
где P(x) означает многочлен n-й степени.
Применяя формулу (2) к интегралам первой группы, за u следует принять многочлен P(x), а за dv – остальную часть подынтегрального выражения. В интегралах второй группы за u принимается lnx, arcsinx, arccosx, arctgx, arcctgx, а за dv – выражение P(x)dx.
Рассмотренные общие методы интегрирования применяются нешаблонно. Кроме того, часто бывают необходимы предварительные алгебраические преобразования подинтегральной функции. Каждый интеграл требует индивидуального подхода, необходимы определенные навыки в интегрировании, а часто и сообразительность. Однако имеются и типовые приемы преобразований определенных видов или классов подинтегральных функций для приведения их к табличным интегралам или для последующего применения общих методов интегрирования. Рассмотрим интегрирование некоторых видов таких функций: простейших рациональных дробей, простейших иррациональностей и тригонометрических функций.
Лекция 4. Определенный интеграл, его свойства и вычисление
| Site: | Навчальний сайт ХНАДУ |
| Course: | Высшая математика (2 семестр) |
| Book: | Лекция 4. Определенный интеграл, его свойства и вычисление |
| Printed by: | Guest user |
| Date: | Tuesday, 30 April 2019, 12:50 AM |
Table of contents
1. Понятие определенного интеграла
Пусть функция y = f( x ) определена на отрезке [ a, b ], a . Выполним следующие операции:
2) в каждом из частичных отрезков [ x i—1, x i ], i = 1, 2, . n, выберем произвольную точку и вычислим значение функции в этой точке: f( zi ) ;
4) составим интегральную сумму функции y = f( x ) на отрезке [ a, b ]:
5) найдем предел интегральной суммы, когда λ → 0.
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка [ a, b ] на частичные отрезки, ни от выбора точек zi в них, то этот предел называется определенным интегралом от функции y = f( x ) на отрезке [ a, b ] и обозначается
В этом случае функция f( x ) называется интегрируемой на [ a, b ]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f( x ) – подынтегральной функцией, f( x ) dx – подынтегральным выражением, x – переменной интегрирования; отрезок [ a, b ] называется промежутком интегрирования.
Теорема 1. Если функция y = f( x ) непрерывна на отрезке [ a, b ], то она интегрируема на этом отрезке.
Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
Если a > b , то, по определению, полагаем
2. Геометрический смысл определенного интеграла
Пусть на отрезке [ a, b ] задана непрерывная неотрицательная функция y = f( x ) . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f( x ) , снизу – осью Ох, слева и справа – прямыми x = a и x = b (рис. 2).
Определенный интеграл от неотрицательной функции y = f( x ) с геометрической точки зрения равен площади криволинейной трапеции, ограниченной сверху графиком функции y = f( x ) , слева и справа – отрезками прямых x = a и x = b , снизу – отрезком оси Ох.
3. Основные свойства определенного интеграла
1. Значение определенного интеграла не зависит от обозначения переменной интегрирования:
2. Постоянный множитель можно выносить за знак определенного интеграла:
3. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
5. (теорема о среднем). Если функция y = f( x ) непрерывна на отрезке [ a, b ], то на этом отрезке существует точка , такая, что
4. Формула Ньютона–Лейбница
Теорема 2. Если функция y = f( x ) непрерывна на отрезке [ a, b ] и F(x) – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
которая называется формулой Ньютона–Лейбница. Разность F(b) — F(a) принято записывать следующим образом:
где символ называется знаком двойной подстановки.
Таким образом, формулу (2) можно записать в виде:
Пример 1. Вычислить интеграл
Решение. Для подынтегральной функции f( x ) = x 2 произвольная первообразная имеет вид
Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид:
5. Замена переменной в определенном интеграле
Теорема 3. Пусть функция y = f( x ) непрерывна на отрезке [ a, b ]. Если:
1) функция x = φ ( t ) и ее производная φ ‘( t ) непрерывны при ;
2) множеством значений функции x = φ ( t ) при является отрезок [ a, b ];
3) φ ( a ) = a , φ ( b ) = b , то справедлива формула
которая называется формулой замены переменной в определенном интеграле.
В отличие от неопределенного интеграла, в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования α и β (для этого надо решить относительно переменной t уравнения φ ( t ) = a и φ ( t ) = b ).
Вместо подстановки x = φ ( t ) можно использовать подстановку t = g( x ) . В этом случае нахождение новых пределов интегрирования по переменной t упрощается: α = g( a ) , β = g( b ) .
Пример 2. Вычислить интеграл
Решение. Введем новую переменную по формуле . Возведя в квадрат обе части равенства , получим 1 + x = t 2 , откуда x = t 2 — 1, dx = ( t 2 — 1)’ dt = 2tdt . Находим новые пределы интегрирования. Для этого в формулу подставим старые пределы x = 3 и x = 8. Получим: , откуда t = 2 и α = 2; , откуда t = 3 и β = 3. Итак,
6. Интегрирование по частям
Теорема 4. Пусть функции u = u( x ) и v = v( x ) имеют непрерывные производные на отрезке [ a, b ]. Тогда имеет место следующая формула интегрирования по частям:
Пример 3. Вычислить
Решение. Пусть u = ln x , тогда , v = x . По формуле (4)
Занятие Интегральное исчисление Неопределенный интеграл и его геометрический смысл. Основные свойства неопределенного интеграла
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Занятие 2. Интегральное исчисление
Неопределенный интеграл и его геометрический смысл. Основные свойства неопределенного интеграла.
Основные методы интегрирования неопределенного интеграла.
Определенный интеграл и его геометрический смысл.
Формула Ньютона-Лейбница. Методы вычисления определенного интеграла.
Зная производную или дифференциал функции, можно найти саму эту функцию (восстановить функцию). Такое действие, обратное дифференцированию, называется интегрированием.
Первообразной функцией по отношению к данной функции 

Для данной функции 


Совокупность всех первообразных 




Геометрический смысл неопределенного интеграла. Геометрически, неопределенный интеграл представляет собой семейство интегральных кривых на плоскости, полученных путем параллельного переноса графика функции 
Основные свойства неопределённого интеграла
Свойство 1. Производная неопределенного интеграла равна подынтегральной функции:
Свойство 2. Дифференциал неопределенного интеграла равен подынтегральному выражению:
Свойство 3. Интеграл от дифференциала функции равен этой функции плюс const:
Свойство 4. Линейность интеграла.
Таблица основных интегралов
Основные методы интегрирования
Непосредственное интегрирование – это метод, основанный на применении тождественных преобразований подынтегральной функции, а также основных свойств неопределенного интеграла и табличных интегралов. Наиболее часто используются следующие преобразования подынтегральной функции:
деление числителя на знаменатель почленно;
применение формул сокращенного умножения;
применение тригонометрических тождеств.
Замена переменной (метод подстановки) – это метод, заключающийся во введении новой переменной с целью преобразования данного интеграла в табличный. Чаще всего этот метод используется, если в подынтегральном выражении содержится сложная функция, тогда ее промежуточный аргумент и надо обозначить как новую переменную, например 
найти дифференциал новой переменной 
записать прежний интеграл, используя только переменную 

используя таблицу интегралов, записать решение для подынтегральной функции 
осуществить обратную подстановку, заменив переменную 
Метод интегрирования по частям – это метод, заключающийся в использовании формулы:

Этот метод применяется в том случае, если интеграл 











Рассмотрим некоторую функцию 

1. Разобьём промежуток 





2. На каждом частичном участке 


3. Составим произведение
4. Составим сумму 
5. Измельчая дробление (за счёт увеличения числа точек дробления 


Если этот предел существует, не зависит от способа дробления и выбора точек 



Геометрический смысл определенного интеграла. Допустим, что функция 





причём, это равенство будет тем точнее, чем мельче дробление, и в пределе при n →+∞ и λ → 0 мы получим:

В этом и заключается геометрический смысл определённого интеграла.
Основные свойства определённого интеграла
Свойство 1. Определенный интеграл с одинаковыми пределами равен нулю.
Свойство 2. При перемене местами пределов интегрирования определённый интеграл меняет знак на противоположный.
Свойство 3. Линейность интеграла.
С





Теорема. Если функция 



Эта формула сводит нахождение определенных интегралов к нахождению неопределенных интегралов. Разность 

Рассмотрим основные способы вычисления определённого интеграла: замену переменных (подстановку) и интегрирование по частям.
Подстановка (замена переменной) в определённом интеграле — необходимо выполнить следующие действия:
ввести новую переменную 
найти дифференциал новой переменной 
вычислить новые значения пределов интегрирования:


записать прежний интеграл, используя только переменную 


используя таблицу интегралов, записать решение для полученной подынтегральной функции;
применив формулу Ньютона-Лейбница, вычислить значение определенного интеграла.
Замечание. При вычислении определённых интегралов с помощью подстановки нет необходимости возвращаться к первоначальному аргументу.
2. Интегрирование по частям в определённом интеграле сводится к применению формулы:

Примеры решения задач
Задание 1. Найти неопределенный интеграл методом непосредственного интегрирования.
1. 

Задание 2. Найти неопределенный интеграл, используя метод замены переменной.
1. 


Таким образом, мы получили неопределенный интеграл табличного вида: степенная функция. Используя правило нахождения неопределенного интеграла от степенной функции, найдем:
Сделав обратную замену, получим окончательный ответ:
Задание 3. Найти неопределенный интеграл, используя метод интегрирования по частям.
1. 
Тогда дифференцируя первое выражение и интегрируя второе, получим:
Теперь подставив в формулу метода интегрирования по частям введенные нами обозначения и, получим:
Задание 4. Вычислить определенный интеграл.





Задания для самостоятельного решения
Решить неопределенные интегралы:




- http://life-prog.ru/2_15288_neopredelenniy-integral.html
- http://mirznanii.com/a/315545/opredelennyy-integral
- http://lektsia.com/7x3fcf.html
- http://dl.khadi.kharkov.ua/mod/book/tool/print/index.php?id=22223
- http://gigabaza.ru/doc/142126.html