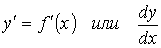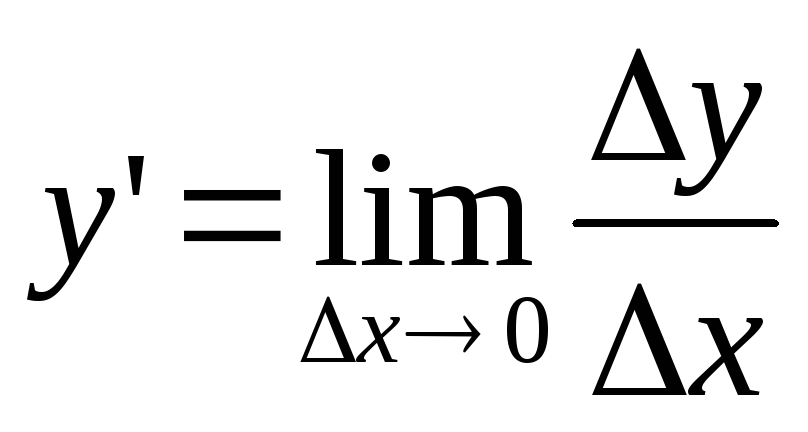С физической точки зрения производная это

Математические задачи находят своё применение во многих науках. К таковым следует отнести не только физику, химию, технику и экономику, но также медицину, экологию и прочие дисциплины. Одним из важных понятий, которое следует освоить, чтобы находить решения важных дилемм, является производная функции. Физический смысл её объяснить совсем не так сложно, как может показаться непосвящённому в суть вопроса. Достаточно лишь найти подходящие примеры тому в реальной жизни и обычных бытовых ситуациях. На самом деле любой автомобилист справляется с подобной задачей каждый день, когда смотрит на спидометр, определяя скорость своей машины в конкретное мгновение фиксированного времени. Ведь именно в этом параметре заключена суть физического смысла производной.

Определить скорость движения человека по дороге, зная пройденное расстояние и время в пути, с лёгкостью может любой пятиклассник. Для этого следует первую из заданных величин разделить на вторую. Но не каждый из юных математиков знает о том, что в данный момент находит отношение приращений функции и аргумента. Действительно, если представить движение в виде графика, откладывая по оси ординат путь, а по абсциссе — время, это будет именно так.

Однако скорость пешехода или любого другого объекта, которую мы определяем на большом участке пути, считая движение равномерным, вполне может меняться. В физике известно множество форм движения. Оно может совершаться не только с постоянным ускорением, но замедляться и возрастать произвольным образом. Следует обратить внимание, что в данном случае линией, описывающей перемещение, будет уже не прямая. Графически она может принимать самые сложные конфигурации. Но для любой из точек графика мы всегда можем провести касательную, представленную линейной функцией.

Для уточнения параметра изменения перемещения в зависимости от времени приходится сокращать измеряемые отрезки. Когда же они станут бесконечно малыми, вычисляемая скорость окажется мгновенной. Данный опыт помогает нам дать определение производной. Физический смысл её также логически вытекает из подобных рассуждений.

С точки зрения геометрии

Известно, что чем больше скорость тела, тем круче график зависимости перемещения от времени, а значит, и угол наклона касательной к графику в какой-то определённой точке. Показателем подобных изменений может стать тангенс угла между осью абсцисс и линией касательной. Как раз он определяет значение производной и вычисляется отношением длин противолежащего к прилежащему катету в прямоугольном треугольнике, образованном перпендикуляром, опущенным из некоторой точки на ось абсцисс.

В этом заключается геометрический смысл первой производной. Физический же раскрывается в том, что величина противолежащего катета в нашем случае представляет собой пройденный путь, а прилежащего – время. При этом отношением их является скорость. И снова мы приходим к выводу, что мгновенная скорость, определяемая при стремлении обоих промежутков к бесконечно малому, и является сутью понятия производной, указывая на её физический смысл. Второй производной в данном примере будет ускорение тела, демонстрирующее, в свою очередь, степень изменения скорости.

Примеры нахождения производных в физике

Производная – это показатель скорости изменения любой функции, даже когда речь не идёт о движении в прямом смысле слова. Чтобы наглядно продемонстрировать это, приведём несколько конкретных примеров. Допустим, сила тока, завися от времени, изменяется согласно следующему закону: I = 0,4t 2 . Требуется найти значение скорости, с которой происходит изменение этого параметра в конце 8-й секунды процесса. Заметим, что сама искомая величина, как можно судить из уравнения, постоянно возрастает.

Для решения требуется найти первую производную, физический смысл которой был рассмотрен ранее. Здесь dI/dt = 0,8t. Далее найдём оную при t=8, получим, что скорость, с которой происходит изменение силы тока, равна 6,4 A/c. Здесь считается, что сила тока измеряется в амперах, а время, соответственно, в секундах.

Всё изменчиво

Видимый окружающий мир, состоящий из материи, постоянно претерпевает изменения, находясь в движении протекающих в нём разнообразных процессов. Для описания их можно использовать самые разные параметры. Если они объединены зависимостью, то математически записываются в виде функции, наглядно показывающей их изменения. А где есть движение (в каком бы виде оно ни выражалось), там существует и производная, физический смысл которой мы и рассматриваем в настоящий момент.

По этому поводу следующий пример. Допустим, температура тела изменяется по закону T=0,2t 2 . Следует найти скорость его нагревания в конце 10-й секунды. Решение задачи производится способом, аналогичным описанному в предыдущем случае. То есть мы находим производную и подставляем в неё значение для t = 10, получаем T = 0,4t = 4. Значит, окончательным ответом считается 4 градуса за секунду, то есть процесс нагревания и изменение температуры, измеряемой в градусах, происходит именно с такой скоростью.

Решение практических задач

Конечно, в реальной жизни всё бывает гораздо сложнее, чем в теоретических задачах. На практике значение величин определяется обычно в ходе эксперимента. При этом используются приборы, которые выдают показания при измерениях с определённой погрешностью. Поэтому при вычислениях приходится иметь дело с приближёнными значениями параметров и прибегать к округлениям неудобных чисел, а также другим упрощениям. Приняв это ко вниманию, снова приступим к задачам на физический смысл производной, учитывая, что они являются лишь некоей математической моделью происходящих в природе сложнейших процессов.

Извержение вулкана

Представим, что происходит извержение вулкана. Насколько он может быть опасен? Для выяснения этого вопроса необходимо рассмотреть множество факторов. Мы постараемся учесть один из них.

Из жерла «огненного чудовища» выбрасываются вертикально вверх камни, имеющие начальную скорость с момента выхода наружу 120 м/с. Необходимо просчитать, какой они могут достигнуть максимальной высоты.

Для нахождения искомого значения составим уравнение зависимости высоты H, измеряемой в метрах, от прочих величин. К таковым относятся начальная скорость и время. Значение ускорения считаем известным и приблизительно равным 10 м/с 2 .

Частная производная

Рассмотрим теперь физический смысл производной функции немного с другой стороны, ведь само уравнение может содержать не одну, а несколько переменных. К примеру, в предыдущей задаче зависимость высоты подъёма камней, выбрасываемых из жерла вулкана, определялась не только изменением временных характеристик, но и значением начальной скорости. Последняя считалась постоянной, фиксированной величиной. Но в других задачах с совершенно иными условиями всё могло быть иначе. Если величин, от которых зависит сложная функция, несколько, расчёты производятся согласно указанным ниже формулам.

Физический смысл частой производной следует определять, как и в обычном случае. Это скорость изменения функции в некоторой определённой точке при росте параметра переменной. Она вычисляется таким образом, что все остальные составляющие принимаются за постоянные, лишь только один рассматривается как переменная. Далее всё происходит по обычным правилам.

Незаменимый советник по многим вопросам

Понимая физический смысл производной, примеры решения запутанных и сложных проблем, ответ в которых позволяют найти подобные знания, привести несложно. Если у нас есть функция, описывающая расход горючего в зависимости от скорости автомобиля, можем рассчитать, при каких параметрах последней расход бензина будет наименьшим.

В медицине можно предвидеть, каким образом будет реагировать человеческий организм на прописанное врачом лекарство. Приём препарата сказывается на самых разных физиологических показателях. К ним относятся изменения артериального давления, пульса, температуры тела и многого другого. Все они зависят от дозы принимаемого лекарственного средства. Данные расчёты помогают предвидеть ход лечения, как в благоприятных проявлениях, так и в нежелательных случайностях, способных фатальным образом отразиться на изменениях в организме больного.

Несомненно, важным оказывается понимание физического смысла производной в технических вопросах, в частности в электротехнике, электронике, конструировании и строительстве.

Тормозной путь

Рассмотрим очередную задачу. Двигаясь с постоянной скоростью, автомобиль, приближаясь к мосту, за 10 секунд до въезда вынужден был затормозить, так как водитель заметил дорожный знак, запрещающий движение со скоростью более 36 км/час. Не нарушил ли правила шофёр, если тормозной путь его можно описать формулой S = 26t – t 2 ?

Вычислив первую производную, найдём формулу для скорости, получим v = 28 – 2t. Далее подставим в указанное выражение значение t=10.

Так как эта величина была выражена в секундах, скорость оказывается равной 8 м/с, а значит, 28,8 км/час. Это даёт возможность понять, что шофёр начал тормозить вовремя и не нарушил правила движения, а значит, и предел указанной на знаке скорости.

Подобное доказывает важность физического смысла производной. Пример решения данной задачи демонстрирует широту использования этого понятия в самых разных сферах жизни. В том числе и в бытовых ситуациях.

Производная в экономике

До XIX столетия экономисты в основном оперировали средними величинами, будь то производительность труда или цена на выпускаемую продукцию. Но с некоторого момента для составления эффективных прогнозов в данной области больше стали необходимы предельные величины. К таковым можно отнести предельную полезность, доход или издержки. Понимание этого дало толчок к созданию совершенно нового инструмента в экономических исследованиях, который существует и развивается вот уже более ста лет.

Для составления подобных расчётов, где главенствуют такие понятия, как минимум и максимум, просто необходимо понимание геометрического и физического смысла производной. Среди создателей теоретической основы указанных дисциплин можно назвать таких видных английских и австрийских экономистов, как У. С. Джевонс, К. Менгер и других. Конечно, предельные величины в экономических выкладках не всегда использовать удобно. А, к примеру, квартальные отчёты не обязательно укладываются в существующую схему, но всё же применение подобной теории во многих случаях бывает полезно и эффективно.

Производная в физике

Разделы: Математика

Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают.

Межпредметные связи являются дидактическим условием и средством глубокого и всестороннего усвоения основ наук в школе.
Кроме того, они способствуют повышению научного уровня знаний учащихся, развитию логического мышления и их творческих способностей. Реализация межпредметных связей устраняет дублирование в изучении материала, экономит время и создаёт благоприятные условия для формирования общеучебных умений и навыков учащихся.
Установление межпредметных связей в курсе физики повышает эффективность политехнической и практической направленности обучения.
В преподавании математики очень важна мотивационная сторона. Математическая задача воспринимается учащимися лучше, если она возникает как бы у них на глазах, формулируется после рассмотрения каких-то физических явлений или технических проблем.
Сколько бы ни говорил учитель о роли практики в прогрессе математики и о значении математики для изучения физики, развития техники, но если он не показывает, как физика влияет на развитие математики и как математика помогает практике в решении её проблем, то развитию материалистического мировоззрения будет нанесен серьёзный ущерб. Но для того, чтобы показать, как математика помогает в решении её проблем, нужны задачи, не придуманные в методических целях, а возникающие на самом деле в различных областях практической деятельности человека

Исторические сведения

Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:

о разыскании касательной к произвольной линии;
о разыскании скорости при произвольном законе движения.

Еще раньше понятие производной встречалось в работах итальянского математика Николо Тартальи (около 1500 – 1557гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.

Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л.Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Термин «производная» является буквальным переводом на русский французского слова derive, которое ввел в1797 году Ж. Лагранж (1736-1813).
И.Ньютон называл производную функцию флюксией, а саму функцию – флюентой.

Некоторые применения производной в физике

Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции.

Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Таким образом,

Значит, чтобы вычислить производную функции f(x) в точке x по определению, нужно:

найти разность
найти отношение
найти предел этого отношения при ,

Рассмотрим несколько физических задач, при решении которых применяется эта схема.

Задача о мгновенной скорости. Механический смысл производной

Напомним, как определялась скорость движения. Материальная точка движется по координатной прямой. Координата х этой точки есть известная функция x(t) времени t. За промежуток времени от t до t + перемещение точки равно x(t + ) – x(t) – а её средняя скорость такова: .
Обычно характер движения бывает таковым, что при малых , средняя скорость практически не меняется, т.е. движение с большой степенью точности можно считать равномерным. Другими словами, значение средней скорости при стремится к некоторому вполне определённому значению, которое называют мгновенной скоростью v(t) материальной точки в момент времени t.

Итак,

Но по определению
Поэтому считают, что мгновенная скорость в момент времени t

Коротко говорят: производная координаты по времени есть скорость. В этом состоит механический смысл производной.

Аналогично рассуждая, получаем, что производная от скорости по времени есть ускорение, т.е.

Задача о теплоемкости тела

Чтобы температура тела массой в 1г повысилась от 0 градусов до t градусов, телу необходимо сообщить определенное количество тепла Q. Значит, Q есть функция температуры t, до которой тело нагревается: Q = Q(t). Пусть температура тела повысилась с t до t. Количество тепла, затраченное для этого нагревания, равно Отношение есть количество тепла, которое необходимо в среднем для нагревания тела на 1 градус при изменении температуры на градусов. Это отношение называется средней теплоёмкостью данного тела и обозначается с_ср.
Т.к. средняя теплоёмкость не дает представления о теплоёмкости для любого значения температуры Т, то вводится понятие теплоёмкости при данной температуре t (в данной точке t).
Теплоемкостью при температуре t (в данной точке) называется предел

Коротко говорят: производная от количества тепла, получаемого телом, по температуре есть теплоемкость.

Задача о линейной плотности стержня

Рассмотрим неоднородный стержень.

Стержень называют неоднородным, если на два участка одинаковой длины приходятся различные массы.

Для такого стержня встаёт вопрос о скорости изменения массы в зависимости от его длины.

Средняя линейная плотность масса стержня есть функция его длины х.

Таким образом, линейная плотность неоднородного стержня в данной точке определяется следующим образом:

Коротко говорят: линейная плотность стержня в точке есть производная массы по длине.

Рассматривая подобные задачи, можно получить аналогичные выводы по многим физическим процессам. Некоторые из них приведены в таблице.

Функция

Формула

Вывод

m(t) – зависимость массы расходуемого горючего от времени. Производная массы по времени есть скорость расхода горючего. T(t) – зависимость температуры нагреваемого тела от времени. Производная температуры по времени есть скорость нагрева тела. m(t) – зависимость массы при распаде радиоактивного вещества от времени. Производная массы радиоактивного вещества по времени есть скорость радиоактивного распада. q(t) – зависимость количества электричества, протекающего через проводник, от времени Производная количества электричества по времени есть сила тока. A(t) – зависимость работы от времени Производная работы по времени есть мощность.

Практические задания:

№1.

Снаряд, вылетевший из пушки, движется по закону x(t) = – 4t 2 + 13t (м). Найти скорость снаряда в конце 3 секунды.

№2.

Количество электричества, протекающего через проводник, начиная с момента времени t = 0 c, задаётся формулой q(t) = 2t 2 + 3t + 1 (Кул) Найдите силу тока в конце пятой секунды.

№3.

Количество тепла Q (Дж), необходимого для нагревания 1 кг воды от 0 o до t o С, определяется формулой Q(t) = t + 0,00002t 2 + 0,0000003t 3 . Вычислите теплоемкость воды, если t = 100 o .

№4.

Тело движется прямолинейно по закону х(t) = 3 + 2t + t 2 (м). Определите его скорость и ускорение в моменты времени 1 с и 3 с.

№ 5.

Найдите величину силы F, действующей на точку массой m, движущуюся по закону х(t) = t 2 – 4t 4 (м), при t = 3 с.

№ 6.

Тело, масса которого m = 0,5кг, движется прямолинейно по закону х(t) = 2t 2 + t – 3 (м). Найдите кинетическую энергию тела через 7 с после начала движения.

Заключение

Можно указать еще много задач из техники, для решения которых также необходимо отыскивать скорость изменения соответствующей функции.
Например, отыскание угловой скорости вращающегося тела, линейный коэффициент расширения тел при нагревании, скорость химической реакции в данный момент времени.
Ввиду обилия задач, приводящих к вычислению скорости изменения функции или, иначе, к вычислению предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, оказалось необходимым выделить такой предел для произвольной функции и изучить его основные свойства. Этот предел и назвали производной функции.

Итак, на ряде примеров мы показали, как различные физические процессы описываются с помощью математических задач, каким образом анализ решений позволяет делать выводы и предсказания о ходе процессов.
Конечно, число примеров такого рода огромно, и довольно большая часть из них вполне доступна интересующимся учащимся.

“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Список литературы :

Абрамов А.Н., Виленкин Н.Я. и др. Избранные вопросы математики. 10 класс. – М: Просвещение, 1980.
Виленкин Н.Я., Шибасов А.П. За страницами учебника математики. – М: Просвещение,1996.
Доброхотова М.А., Сафонов А.Н. Функция, её предел и производная. – М: Просвещение, 1969.
Колмогоров А.Н., Абрамов А.М. и др. Алгебра и начала математического анализа. – М: Просвещение, 2010.
Колосов А.А. Книга для внеклассного чтения по математике. – М: Учпедгиз, 1963.
Фихтенгольц Г.М. Основы математического анализа, ч.1 – М: Наука, 1955.
Яковлев Г.Н. Математика для техникумов. Алгебра и начала анализа, ч.1 – М: Наука, 1987.

Лекция 2. Физический и геометрический смысл первой и второй производной

2.1. Вторая производная – это производная от производной функции; обозначается двумя штрихами т.е. .

Например, для функции .

Вторая производная для первой производной является такой же характеристикой, как первая производная для самой функции. Она характеризует характер монотонности производной и точки экстремума производной. Вторая производная помогает точнее определять поведение функции на отрезке (или на области определения). Исследование функции при помощи второй производной происходит согласно порядку, уже определенному выше. А именно, нужно искать точки, в которых вторая производная обращается в нуль или не существует. Как правило, их называют критические точки второго рода.

Обратите внимание, что для рациональных функций при нахождении последовательно первой и второй производных, степень функции понижается каждый раз на порядок. Т.е., если исследуемая функция третьей степени, то ее первая производная меняется по квадратичному закону, а вторая – по линейному.

А для тригонометрических функций синус и косинус, вторая производная фактически превращается обратно в саму функцию. Например: .

2.2. Физический смысл первой и второй производной

С точки зрения механики. Если задан закон, по которому путь (или перемещение) материальной точки зависит от переменной – времени, т.е. S (t), x(t), тогда: первая производная показывает скорость изменения перемещения, а вторая производная – скорость изменения скорости движения, т.е. ускорение.

или

Равномерное движение: (скорость постоянна, ускорение равно нулю);
Равноускоренное движение:(скорость меняется по линейному закону, ускорение постоянно)

Пример. Движение материальной точки осуществляется по закону .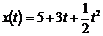

Найдите: а) начальную скорость движения v; б) ускорение движения a(t); в) время, через которое скорость точки станет равной 12.

Решение. а) б) в)

2.3. Геометрический смысл первой и второй производной

2.3.1. Первая производная. Значение производной в точке x равно угловому коэффициенту касательной, построенной к графику соответствующей функции в точке с абсциссой x:

, α – угол наклона касательной к оси абсцисс.

2.3.2. Вторая производная.

«Наглядным свойством графика функции на некотором промежутке является его выпуклость. График функции может иметь выпуклость как вверх (например, у функции ), так и выпуклость вниз (например, у функции ).

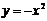
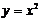
Точка, в которой меняется характер выпуклости, называется точкой перегиба функции.

Простейший пример – это функция : для нее точка x=0 является точкой перегиба.

Если в этой точке провести касательную, то по одну сторону от точки перегиба график функции начинает уходить выше касательной (становится выпуклым вниз), а по другую сторону — график уходит вниз (становится выпуклым вверх).

Точки перегиба появляются в том случае, если первая производная при переходе через эту точку обратилась в нуль или не существовала, но знак не поменяла.

Например: 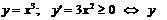монотонно возрастает. При этом вторая производная: в точке 0 меняет знак; при — выпуклость вверх, при — выпуклость вниз.

В общем виде алгоритм нахождения точек перегиба:

· Найти вторую производную функции ;

· Найти критические точки второго рода, т.е. приравнять вторую производную к нулю и решить уравнение ;

· Определить знаки второй производной на получившихся промежутках;

· По знаку второй производной сделать выводы о наличии точек перегиба: это критические точки, в которых вторая производная меняет знак;

Если на промежутке — график функции имеет выпуклость вниз ( );

Если на промежутке — график функции имеет выпуклость вверх ( )

2.4. Задачи

Найти точки перегиба функции и определить выпуклость графика:

Вывод: x=0 – точка перегиба: выпуклость графика – вверх;

— выпуклость графика – вниз.

Критических точек второго рода бесконечно много. Однако, учитывая, что наименьший период функции равен π, достаточно определить наличие точек перегиба на этом периоде:

Определение знаков второй производной:

Вывод: точки перегиба .

В точках — перегиб с выпуклости графика вверх на выпуклость вниз;

В точках — перегиб с выпуклости графика вниз на выпуклость вверх.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 9491 — | 6697 — или читать все.

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

1. Понятие производной

При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом

Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f ‘ (x), называют дифференцированием и состоит он из следующих трех шагов: 1) даем аргументу x приращение x и определяем соответствующее приращение функции y = f(x+x) -f(x); 2) составляем отношение

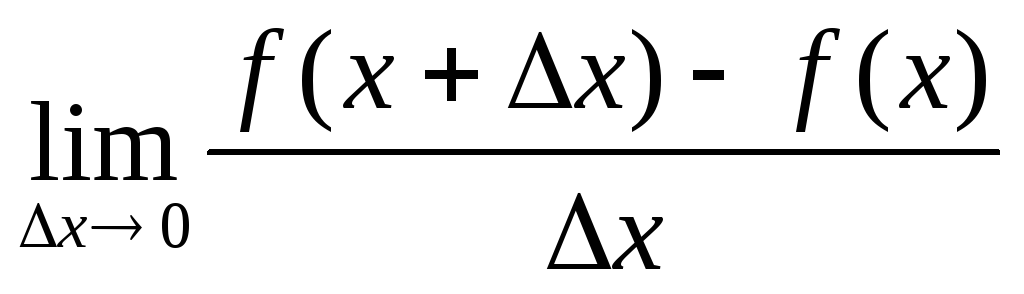
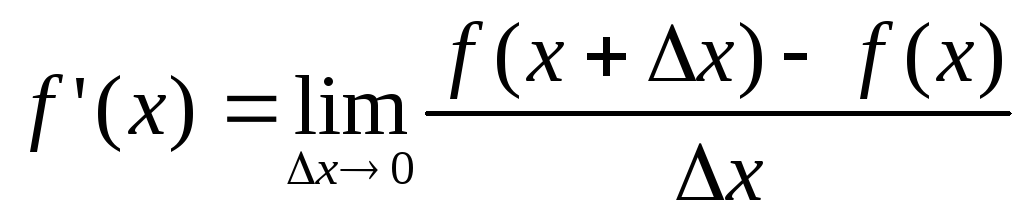
3) считая x постоянным, а x 0, находим, который обозначаем черезf ‘ (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу. Определение: Производной y ‘ =f ‘ (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен. Таким образом, , или

Заметим, что если при некотором значении x, например при x=a, отношение 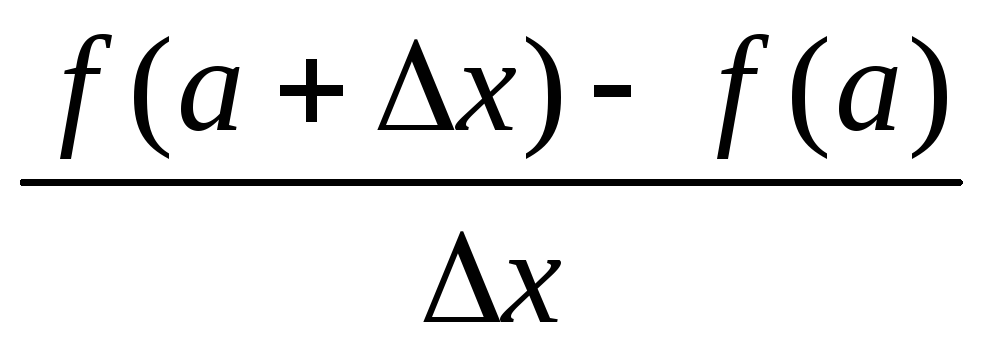приx0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.

2. Геометрический смысл производной.

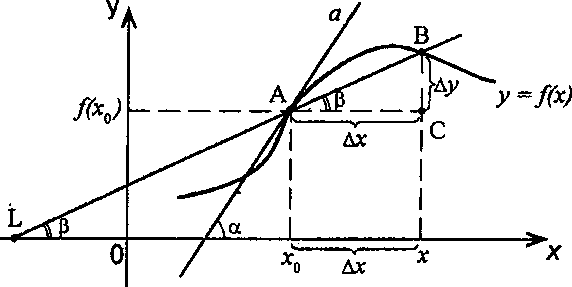
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x

Рассмотрим произвольную прямую, проходящую через точку графика функции — точку А(x, f (х)) и пересекающую график в некоторой точке B(x;f(x)). Такая прямая (АВ) называется секущей. Из ∆АВС: АС = ∆x; ВС =∆у; tgβ=∆y/∆x .

Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO — это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k — угловой коэффициент прямой АВ.

Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.

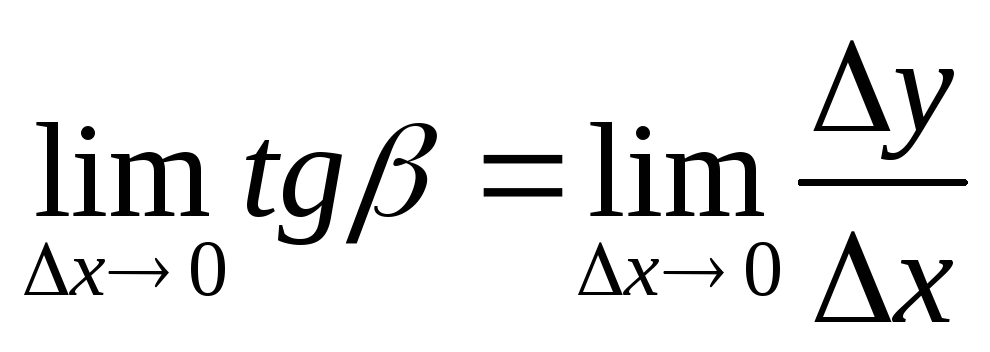
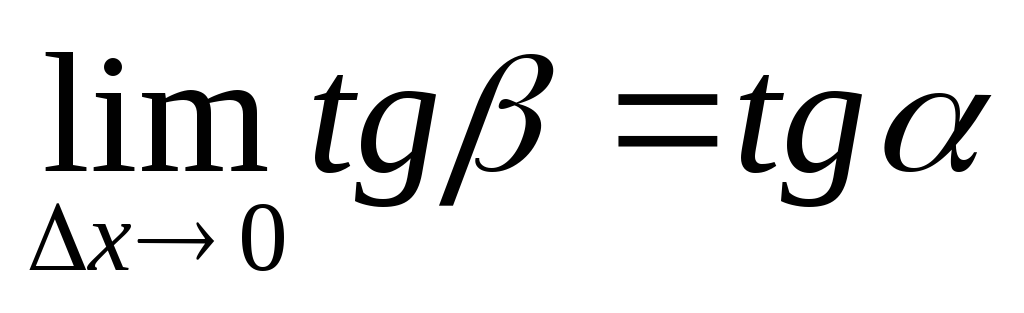
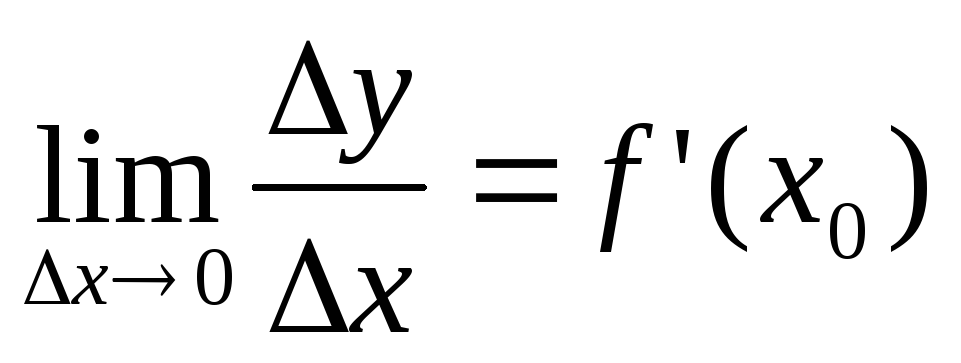
Если перейти к пределу при ∆х → 0 в равенстве tgβ =∆y/∆x, то получимилиtg =f ‘(x), так как -угол наклона касательной к положительному направлению оси Ох , по определению производной. Но tg = k — угловой коэффициент касательной, значит, k = tg = f ‘(x).

Итак, геометрический смысл производной заключается в следующем:

Производная функции в точке xравна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x.

3. Физический смысл производной.

Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t; t+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.

Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.

lim Vср (t) = (t) — мгновенная скорость в момент времени t, ∆t → 0.

а lim = ∆x/∆t = x'(t) (по определению производной).

Физический смысл производной заключается в следующем: производная функции y = f(x) в точке x— это скорость изменения функции f (х) в точке x

Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.

(t) = x'(t) — скорость,

a(f) = '(t) — ускорение, или

Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:

φ = φ(t) — изменение угла от времени,

ω = φ'(t) — угловая скорость,

ε = φ'(t) — угловое ускорение, или ε = φ»(t).

Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:

x  [0; l], l — длина стержня,

р = m'(х) — линейная плотность.

С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука

F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω 2 =k/m, получим дифференциальное уравнение пружинного маятника х»(t) + ω 2 x(t) = 0,

где ω = √k/√m частота колебаний (l/c), k — жесткость пружины (H/m).

Уравнение вида у» + ω 2 y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция

у = Asin(ωt + φ) или у = Acos(ωt + φ), где

А — амплитуда колебаний, ω — циклическая частота,

Физический смысл производной

Физический смысл производной заключается в том, что мгновенная скорость материальной точки в определенный момент времени $ t_0 $ равна производной закона движения $ s(t_0) $ этой точки в момент времени $ t_0 $:

Примеры решения

Определение

Скорость точки равна производной пути по времени:

$$ v(t) = s'(t) = (4t^2+2t+1)’ = 8t + 2 $$

Мгновенная скорость в момент времени $ t_0 = 2 $:

$$ v(t_0) = v(2) = 8 \cdot 2 + 2 = 16 + 2 = 18 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Пример 1

Найти мгновенную скорость движения материальной точки в момент времени $ t_0 = 2 c $, если точка движется по закону $ s(t) = 4t^2+2t+1 $

Решение

Ответ

$$ v = 18 \text $$

Используя физический смысл производной, находим закон изменения скорости материальной точки: $$ v(t) = s'(t) = (3t^2-3t-5)’ = 6t — 3 $$

Чтобы найти момент времени $ t_0 $, в который скорость будет равной трём, нужно составить и решить уравнение $ v(t_0) = 3 $:

$$ 6t_0 — 3 = 3 $$ $$ 6t_0 = 6 $$ $$ t_0 = 1 $$

Понятие производной

Производная

Производная — это скорость изменения функции. Она показывает, как сильно будет изменяться значение функции при небольшом изменении переменной. Теперь дадим формальное определение.

Геометрический смысл производной

Геометрический смысл производной применяется при исследовании свойств функций:

Используя геометрический смысл, можно по графику функции найти производную в точке. Для этого необходимо провести касательную и отметить на ней любые две точки (удобно использовать точки с целыми координатами). Если ( x 1 ; y 1 ) (x_1;y_1) ( x 1 ; y 1 ) — координаты первой точки, а ( x 2 ; y 2 ) (x_2;y_2) ( x 2 ; y 2 ) — координаты второй точки, то производная равна y 2 − y 1 x 2 − x 1 \fracx 2 − x 1 y 2 − y 1 .

Уравнение касательной

Физический смысл производной

Приведем несколько других примеров из физики .

Как решать задачи на физический смысл производной

Первый шаг — это вычисление производной в соответствии с правилами дифференцирования.

После этого можно найти скорость в определенный момент времени, подставив соответствующее значение t t t .

Если же нужно найти момент времени, когда достигалась определенная скорость v 0 v_0 v 0 , то нужно решить уравнение x ′ ( t ) = v 0 x'(t)=v_0 x ′ ( t ) = v 0 относительно t t t .

Применим этот подход при решении следующей задачи:

Производная функции. Исчерпывающее руководство (2019)

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Представим себе прямую дорогу, проходящую по холмистой местности. То есть она идет то вверх, то вниз, но вправо или влево не поворачивает. Если ось направить вдоль дороги горизонтально, а – вертикально, то линия дороги будет очень похожа на график какой-то непрерывной функции:

Ось – это некий уровень нулевой высоты, в жизни мы используем в качестве него уровень моря.

Двигаясь вперед по такой дороге, мы также движемся вверх или вниз. Также можем сказать: при изменении аргумента (продвижение вдоль оси абсцисс) изменяется значение функции (движение вдоль оси ординат). А теперь давай подумаем, как определить «крутизну» нашей дороги? Что это может быть за величина? Очень просто: на сколько изменится высота при продвижении вперед на определенное расстояние. Ведь на разных участках дороги, продвигаясь вперед (вдоль оси абсцисс) на один километр, мы поднимемся или опустимся на разное количество метров относительно уровня моря (вдоль оси ординат).

Продвижение вперед обозначим (читается «дельта икс»).

Греческую букву (дельта) в математике обычно используют как приставку, означающую «изменение». То есть – это изменение величины , – изменение ; тогда что такое ? Правильно, изменение величины .

Важно: выражение – это единое целое, одна переменная. Никогда нельзя отрывать «дельту» от «икса» или любой другой буквы! То есть, например, .

Итак, мы продвинулись вперед, по горизонтали, на . Если линию дороги мы сравниваем с графиком функции , то как мы обозначим подъем? Конечно, . То есть, при продвижении вперед на мы поднимаемся выше на .

Величину посчитать легко: если в начале мы находились на высоте , а после перемещения оказались на высоте , то . Если конечная точка оказалась ниже начальной, будет отрицательной – это означает, что мы не поднимаемся, а спускаемся.

Вернемся к «крутизне»: это величина, которая показывает, насколько сильно (круто) увеличивается высота при перемещении вперед на единицу расстояния:

Предположим, что на каком-то участке пути при продвижении на км дорога поднимается вверх на км. Тогда крутизна в этом месте равна . А если дорога при продвижении на м опустилась на км? Тогда крутизна равна .

А теперь рассмотрим вершину какого-нибудь холма. Если взять начало участка за полкилометра до вершины, а конец – через полкилометра после него, видно, что высота практически одинаковая.

То есть, по нашей логике выходит, что крутизна здесь почти равна нулю, что явно не соответствует действительности. Просто на расстоянии в км может очень многое поменяться. Нужно рассматривать более маленькие участки для более адекватной и точной оценки крутизны. Например, если измерять изменение высоты при перемещении на один метр, результат будет намного точнее. Но и этой точности нам может быть недостаточно – ведь если посреди дороги стоит столб, мы его можем просто проскочить. Какое расстояние тогда выберем? Сантиметр? Миллиметр? Чем меньше, тем лучше!

В реальной жизни измерять расстояние с точностью до милиметра – более чем достаточно. Но математики всегда стремятся к совершенству. Поэтому было придумано понятие бесконечно малого, то есть величина по модулю меньше любого числа, которое только можем назвать. Например, ты скажешь: одна триллионная! Куда уж меньше? А ты подели это число на – и будет еще меньше. И так далее. Если хотим написать, что величина бесконечно мала, пишем так: (читаем «икс стремится к нулю»). Очень важно понимать, что это число не равно нулю! Но очень близко к нему. Это значит, что на него можно делить.

Понятие, противоположное бесконечно малому – бесконечно большое ( ). Ты уже наверняка сnалкивался с ним, когда занимался неравенствами: это число по модулю больше любого числа, которое только можешь придумать. Если ты придумал самое большое из возможных чисел, просто умножь его на два, и получится еще больше. А бесконечность еще больше того, что получится. Фактически бесконечно большое и бесконечно малое обратны друг другу, то есть при , и наоборот: при .

Теперь вернемся к нашей дороге. Идеально посчитанная крутизна – это куртизна, вычисленная для бесконечно малого отрезка пути, то есть:

Замечу, что при бесконечно малом перемещении изменение высоты тоже будет бесконечно мало. Но напомню, бесконечно малое – не значит равное нулю. Если поделить друг на друга бесконечно малые числа, может получиться вполне обычное число, например, . То есть одна малая величина может быть ровно в раза больше другой.

К чему все это? Дорога, крутизна… Мы ведь не в автопробег отправляемся, а математику учим. А в математике все точно так же, только называется по-другому.

Понятие производной

Производная функции это отношение приращения функции к приращению аргумента при бесконечно малом приращение аргумента.

Приращением в математике называют изменение. То, насколько изменился аргумент ( ) при продвижении вдоль оси , называется приращением аргумента и обозначается То, насколько изменилась функция (высота) при продвижении вперед вдоль оси на расстояние , называется приращением функции и обозначается .

Итак, производная функции – это отношение к при . Обозначаем производную той же буквой, что и функцию, только со штрихом сверху справа: или просто . Итак, запишем формулу производной, используя эти обозначения:

Как и в аналогии с доро́гой здесь при возрастании функции производная положительна, а при убывании – отрицательна.

А бывает ли производная равна нулю? Конечно. Например, если мы едем по ровной горизонтальной дороге, крутизна равна нулю. И правда, высота ведь не совсем меняется. Так и с производной: производная постоянной функции (константы) равна нулю:

так как приращение такой функции равно нулю при любом .

Давай вспомним пример с вершиной холма. Там получалось, что можно так расположить концы отрезка по разные стороны от вершины, что высота на концах оказывается одинаковой, то есть отрезок располагается параллельно оси :

Но большие отрезки – признак неточного измерения. Будем поднимать наш отрезок вверх параллельно самому себе, тогда его длина будет уменьшаться.

В конце концов, когда мы будем бесконечно близко к вершине, длина отрезка станет бесконечно малой. Но при этом он остался параллелен оси , то есть разность высот на его концах равна нулю (не стремится, а именно равна). Значит, производная

Понять это можно так: когда мы стоим на самой вершине, меленькое смещение влево или вправо изменяет нашу высоту ничтожно мало.

Есть и чисто алгебраическое объяснение: левее вершины функция возрастает, а правее – убывает. Как мы уже выяснили ранее, при возрастании функции производная положительна, а при убывании – отрицательна. Но меняется она плавно, без скачков (т.к. дорога нигде не меняет наклон резко). Поэтому между отрицательными и положительными значениями обязательно должен быть . Он и будет там, где функция ни возрастает, ни убывает – в точке вершины.

То же самое справедливо и для впадины (область, где функция слева убывает, а справа – возрастает):

Немного подробнее о приращениях.

Итак, мы меняем аргумент на величину . Меняем от какого значения? Каким он (аргумент) теперь стал? Можем выбрать любую точку, и сейчас будем от нее плясать.

Рассмотрим точку с координатой . Значение функции в ней равно . Затем делаем то самое приращение: увеличиваем координату на . Чему теперь равен аргумент? Очень легко: . А чему теперь равно значение функции? Куда аргумент, туда и функция: . А что с приращением функции? Ничего нового: это по-прежнему величина, на которую изменилась функция:

Потренируйся находить приращения:

Найди приращение функции в точке при приращении аргумента, равном .
То же самое для функции в точке .

Решения:

В разных точках при одном и том же приращении аргумента приращение функции будет разным. Значит, и производная в каждой точке своя (это мы обсуждали в самом начале – крутизна дороги в разных точках разная). Поэтому когда пишем производную, надо указывать, в какой точке:

«Ну ладно, ладно, уже давно понятно, что такое производная! Но как ее применить на практике? Давайте уже возьмем и вычислим какую-нибудь производную, в конце концов!» – скажешь ты. Щас все будет.

Вычисление производных

Начнем с простого.

Это мы уже обсуждали: если функция , где – некое постоянное число, то каким бы ни было приращение аргумента , функция нисколько не изменяется: . А значит,

То есть, произвоная от константы равна нулю:

Степенная функция.

Степенной называют функцию, где аргумент в какой-то степени (логично, да?).

Причем – в любой степени: .

Простейший случай – это когда показатель степени :

Найдем ее производную в точке . Вспоминаем определение производной:

Итак, аргумент меняется с до . Каково приращение функции?

Приращение – это . Но функция в любой точке равна своему аргументу. Поэтому:

Производная от равна :

b) Теперь рассмотрим квадратичную функцию ( ): .

А теперь вспомним, что . Это значит, что значением приращения можно пренебречь, так как оно бесконечно мало, и поэтому незначительно на фоне другого слагаемого:

Итак, у нас родилось очередное правило:

c) Продолжаем логический ряд: .

Это выражение можно упростить по-разному: раскрыть первую скобку по формуле сокращенного умножения куб суммы, или же разложить все выражение на множители по формуле разности кубов. Попробуй сделать это сам любым из предложенных способов.

Итак, у меня получилось следующее:

И снова вспомним, что . Это значит, что можно пренебречь всеми слагаемыми, содержащими :

d) Аналогичные правила можно получить и для больших степеней:

e) Оказывается, это правило можно обобщить для степенной функции с произвольным показателем, даже не целым:

Можно сформулировать правило словами: «степень выносится вперед как коэффициент, а потом уменьшается на ».

Докажем это правило позже (почти в самом конце). А сейчас рассмотрим несколько примеров. Найди производную функций:

;
(двумя способами: по формуле и используя определение производной – посчитав приращение функции);
.

Тригонометрические функции.

Здесь будем использовать один факт из высшей математики:

Доказательство ты узнаешь на первом курсе института (а чтобы там оказаться, надо хорошо сдать ЕГЭ). Сейчас только покажу это графически:

Видим, что при функция не существует – точка на графике выколота. Но чем ближе к значению , тем ближе функция к . Это и есть то самое «стремится».

Впредь будем считать, что при это выражение равно : .

Дополнительно можешь проверить это правило с помощью калькулятора. Да-да, не стесняйся, бери калькулятор, мы ведь не на ЕГЭ еще.

Не забудь перевести калькулятор в режим «Радианы»!

Попробуй теперь сам для и так далее.

и т.д. Видим, что чем меньше , тем ближе значение отношения к .

Убедился? Идем дальше.

a) Рассмотрим функцию . Как обычно, найдем ее приращение:

Превратим разность синусов в произведение. Для этого используем формулу (вспоминаем тему «Формулы тригонометрии»): .

Сделаем замену: . Тогда при бесконечно малом также бесконечно мало: . Выражение для принимает вид:

А теперь вспоминаем, что при выражение . А также, что если бесконечно малой величиной можно пренебречь в сумме (то есть при ).

Итак, получаем следующее правило: производная синуса равна косинусу:

b) Теперь косинус: . Здесь будем использовать формулу разности косинусов: :

Значит, производная косинуса равна минус синусу:

Это базовые («табличные») производные. Вот они одним списком:

Позже мы к ним добавим еще несколько, но эти – самые важные, так как используются чаще всего.

Потренируйся:

Найди производную функции в точке ;
Найди производную функции в точке ;
Найди производную функции .

Решения:

Экспонента и натуральный логарифм.

Есть в математике такая функция, производная которой при любом равна значению самой функции при этом же . Называется она «экспонента», и является показательной функцией

Основание этой функции – константа – это бесконечная десятичная дробь, то есть число иррациональное (такое как ). Его называют «число Эйлера», поэтому и обозначают буквой .

Запомнить очень легко.

Ну и не будем далеко ходить, сразу же рассмотрим обратную функцию. Какая функция является обратной для показательной функции? Логарифм:

В нашем случае основанием служит число :

Такой логарифм (то есть логарифм с основанием ) называется «натуральным», и для него используем особое обозначение : вместо пишем .

Чему равен ? Конечно же, .

Производная от натурального логарифма тоже очень простая:

Примеры:

Найди производную функции .
Чему равна производная функции ?

Ответы: Экспонента и натуральный логарифм – функции уникально простые с точки зрения производной. Показательные и логарифмические функции с любым другим основанием будут иметь другую производную, которую мы с тобой разберем позже, после того как пройдем правила дифференцирования.

Правила дифференцирования

Правила чего? Опять новый термин, опять.

Дифференцирование – это процесс нахождения производной.

Только и всего. А как еще назвать этот процесс одним словом? Не производнование же. Дифференциалом математики называют то самое приращение функции при . Происходит этот термин от латинского differentia — разность. Вот.

При выводе всех этих правил будем использовать две функции, например, и . Нам понадобятся также формулы их приращений:

Всего имеется 5 правил.

Константа выносится за знак производной.

Если – какое-то постоянное число (константа), тогда.

Это правило употребляется чаще всех. Докажем его:

Пусть , или проще .

Пример: Найдите производную функции в точке .

Решение:

Ты сперва сам попробуй решить, а потом посмотри решение.

Итак, константа здесь – это , функция – :

Производная суммы.

Производная суммы равна сумме производных:

Очевидно, это правило работает и для разности: .

Докажем. Пусть , или проще .

Примеры.

Найдите производные функций:

Решения:

Производная произведения

Хм, все сложнее и сложнее. Ну, давай разбираться.

Снова введем новую функцию: , или проще .

Вспомним, о чем говорили в самом начале этого раздела:

Но при приращение любой функции тоже бесконечно мало: . Поэтому последним слагаемым в выражении для производной можно пренебречь:

Примеры:

Докажи правило 0 с помощью правила 2;
Найди производную выражения ;
Найди производную функции .

Решения:

Производная частного.

Здесь все аналогично: введем новую функцию и найдем ее приращение:

Примеры:

Найдите производные функций и ;
Найдите производную функции в точке .

Решения:

Производная показательной функции

Теперь твоих знаний достаточно, чтобы научиться находить производную любой показательной функции, а не только экспоненты (не забыл еще, что это такое?).

Итак, , где – это какое-то число 0,\texta\ne 1 \right)»> .

Мы уже знаем производную функции , поэтому давай попробуем привести нашу функцию к новому основанию :

Для этого воспользуемся простым правилом: . Тогда:

Ну вот, получилось. Теперь попробуй найти производную, и не забудь, что эта функция – сложная.

Вот, проверь себя:

Формула получилась очень похожая на производную экспоненты: как было , так и осталось, появился только множитель , который является просто числом, но не переменной.

Примеры:
Найди производные функций:

Ответы:

Производная логарифмической функции

Здесь аналогично: ты уже знаешь производную от натурального логарифма:

Поэтому, чтобы найти произвольную от логарифма с другим основанием, например, :

Нужно привести этот логарифм к основанию . А как поменять основание логарифма? Надеюсь, ты помнишь эту формулу:

Только теперь вместо будем писать :

В знаменателе получилась просто константа (постоянное число, без переменной ). Производная получается очень просто:

Производные показательной и логарифмической функций почти не встречаются в ЕГЭ, но не будет лишним знать их.

Производная сложной функции.

Что такое «сложная функция»? Нет, это не логарифм, и не арктангенс. Данные функции может быть сложны для понимания (хотя, если логарифм тебе кажется сложным, прочти тему «Логарифмы» и все пройдет), но с точки зрения математики слово «сложная» не означает «трудная».

Представь себе маленький конвейер: сидят два человека и проделывают какие-то действия с какими-то предметами. Например, первый заворачивает шоколадку в обертку, а второй обвязывает ее ленточкой. Получается такой составной объект: шоколадка, обернутая и обвязанная ленточкой. Чтобы съесть шоколадку, тебе нужно проделать обратные действия в обратном порядке.

Давай создадим подобный математический конвейер: сперва будем находить косинус числа, а затем полученное число возводить в квадрат. Итак, нам дают число (шоколадка), я нахожу его косинус (обертка), а ты затем возводишь то, что у меня получилось, в квадрат (обвязываешь ленточкой). Что получилось? Функция . Это и есть пример сложной функции: когда для нахождения ее значения мы проделываем первое действие непосредственно с переменной, а потом еще второе действие с тем, что получилось в результате первого.

Мы вполне можем проделывать те же действия и в обратном порядке: сначала ты возводишь в квадрат, а я затем ищу косинус полученного числа: . Несложно догадаться, что результат будет почти всегда разный. Важная особенность сложных функций: при изменении порядка действий функция меняется.

Другими словами, сложная функция – это функция, аргументом которой является другая функция: .

Для первого примера , .

Второй пример: (то же самое). .

Действие, которое делаем последним будем называть «внешней» функцией, а действие, совершаемое первым – соответственно «внутренней» функцией (это неформальные названия, я их употребляю только для того, чтобы объяснить материал простым языком).

Попробуй определить сам, какая функция является внешней, а какая внутренней:

Ответы:Разделение внутренней и внешней функций очень похоже на замену переменных: например, в функции

производим замену переменных и получаем функцию .

Ну что ж, теперь будем извлекать нашу шоколадку – искать производную. Порядок действий всегда обратный: сначала ищем производную внешней функции, затем умножаем результат на производную внутренней функции. Применительно к исходному примеру это выглядит так:

Итак, сформулируем, наконец, официальное правило:

Алгоритм нахождения производной сложной функции:

Пример 2

Пусть точка движется прямолинейно по закону $ s(t) = 3t^2-3t — 5 $. В какой момент времени скорость точки будет $ v = 3 $ м/с?

Решение

Алгоритм	Пример:
1.Определяем «внутреннюю» функцию, находим ее производную.	Внутренняя функция: .
2.Определяем «внешнюю» функцию, находим ее производную.	Внешняя функция: .
3. Умножаем результаты первого и второго пунктов.	.

Вроде бы все просто, да?

Проверим на примерах:

Решения:

Прямо сейчас рекомендую перейти к теме «Уравнение касательной к графику функции». Там ты разберешь геометрический смысл производной, что поспособствует лучшему ее пониманию.

ПРОИЗВОДНАЯ. КОРОТКО О ГЛАВНОМ

Производная функции — отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента:

Константа выносится за знак производной:

Производная сложной функции:

Алгоритм нахождения производной от сложной функции:

Определяем «внутреннюю» функцию, находим ее производную.
Определяем «внешнюю» функцию, находим ее производную.
Умножаем результаты первого и второго пунктов.

P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для успешной сдачи ЕГЭ, для поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это — не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время.

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Можно воспользоваться нашими задачами (не обязательно) и мы их, конечно, рекомендуем.

Для того, чтобы набить руку с помощью наших задач нужно помочь продлить жизнь учебнику YouClever, который ты сейчас читаешь.

Как? Есть два варианта:

Открой доступ ко всем скрытым задачам в этой статье — Купить статью — 299 руб
Открой доступ ко всем скрытым задачам во всех 99-ти статьях учебника — Купить учебник — 899 руб

Да, у нас в учебнике 99 таких статей и доступ для всех задач и всех скрытых текстов в них можно открыть сразу.

Доступ ко всем скрытым задачам предоставляется на ВСЕ время существования сайта.

И в заключение.

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.