Определение натурального числа с точки зрения аксиоматической теории

Перед тем, как перейти к рассмотрению методики изучения приемов письменного сложения и вычитания в начальных классах, необходимо выявить математические основы изучения арифметических действий, установить их важнейшие законы и правила, также взаимосвязь их компонентов и результатов.

Понятие действия сложения и вычитания в математике можно рассмотреть с двух точек зрения: с позиций аксиоматической теории и теоретико-множественного подхода.

По правилам аксиоматической теории построения множества N определить сложение натуральных чисел можно, используя отношение «непосредственно следовать за». Дадим определение с позиций этой теории: сложением натуральных чисел называется алгебраическая операция, определенная на множестве натуральных чисел N и обладающая свойствами:

Число a+ b называется суммой натуральных чисел чисел a ? b , а сами числа a и b — слагаемыми.

При построении множества Z0 используется тоже определение сложения, в котором меняется только первое свойство

Доказано, что алгебраическая операция, обладающая указанными свойствами единственна и она существует [52, C. 233]

Сложение натуральных чисел обладает свойствами коммутативности и ассоциативности. Раскроем их определения без доказательства.

I. Коммутативный закон сложения (переместительный):

II. Ассоциативный закон сложения (сочетательный):

Остановимся на теоретико-множественном смысле суммы nZ0, Раскроем смысл определения сложения [52, с. 128].

Рассмотрим задачу, которую решают первоклассники: «Петя нашел 4 гриба, а Нина — 3. Сколько всего грибов нашли ребята?» Задача решается при помощи действия сложения: 4+3 = 7. Но как объяснить почему использовано сложение, а не другое действие?

Представим условие задачи наглядно, изобразив каждый гриб, который нашел Петя кружком, а каждый гриб, найденный Ниной, квадратом (рис. 1).

Чтобы ответить на вопрос задачи, надо к грибам Пети добавить (присоединить) грибы Нины, т.е. объединить два множества грибов (рис. 2), и сосчитать, сколько в этом объединении оказалось элементов.

Видим, что сложение целых неотрицательных чисел тесно связано с операцией объединения множеств.

Поэтому с точки зрения теоретико-множественного подхода сумму определяют через объединение непересекающихся множеств.

Определение: суммой целых неотрицательных чисел a и b называют число в объединении непересекающихся множеств A и B, таких, что n (A) = a, n (B) = b:

Объясним, пользуясь данным определением, что 5+2=7. 5- это число элементов некоторого множества А, 2 — число элементов некоторого множества В, причем их пересечение должно быть пусто. Возьмем, например, множества , B=. Объединим их: . Путем пересчета устанавливаем, что n = 7.Следовательно, 5+2 =7.

Действие, при помощи которого находят сумму, называется сложением, а числа, которые складывают, называют слагаемыми.

В начальном курсе математики сложением неотрицательных чисел вводится на основе практических упражнений, связанных с объединением двух множеств предметов (теоретико-множественная терминология и символика при этом не используется). Главным средством раскрытия теоретико-множественного смысла сложения является решение простых арифметических задач. Суть решения одной такой задачи проанализирована выше.

Остановимся на определении вычитания натуральных чисел с точки зрения вышеуказанных теорий.

При аксиоматическом построении теории натуральных чисел сначала дается определение разности, затем вычитания.

Разностью натуральных чисел a и b называется такое натуральное число с, что b +с = a. [52, C.136].

Действие, с помощью которого находится разность чисел a и b называется вычитанием.

Из определения видно, что вычитание — это действие, обратное сложению.

Число a — b называется разностью чисел а и b, число а — уменьшаемым, число в — вычитаемым.

Известно, что алгебраическая операция, удовлетворяющая указанному условию на множестве натуральных чисел, существует не всегда. Есть только необходимое условие существования разности и оно единственно: разность натуральных чисел а и b существует тогда и только тогда, когда b

Исходя из определения разности натуральных чисел и условия его существования, можно обосновать известные правила, связывающие сложение и вычитание натуральных чисел [56, C. 140-141].

1. Вычитание числа из суммы: чтобы вычесть число из суммы

достаточно вычесть это число из одного слагаемого суммы и к полученному результату прибавить другое слагаемое.

Пример: (5768 + 929)668=(5768668) + 929 = 6029.

3. Вычитание суммы из числа: чтобы вычесть сумму из числа, достаточно из этого числа последовательно вычесть каждое слагаемое одно за другим.

4. Вычитание числа из разности: чтобы вычесть число из разности достаточно из уменьшаемого a вычесть сумму двух других чисел.

5. Вычитание разности из числа:

6. Прибавление разности к числу:

7. Прибавление числа к разности: чтобы прибавить число к разности достаточно это число прибавить к уменьшаемому и из полученного результата вычесть вычитаемое.

Раскроем теоретико-множественный смысл разности натуральных чисел.

Раскрытие смысла снова начнем с простой арифметической задачи, которую мы даем учащимся первого класса:

«Около школы посадили 8 деревьев — берез и рябин. Берез 3. Сколько рябин посадили около школы?»

Чтобы ответить на вопрос задачи, надо . Но как объяснить, почему здесь использовано вычитание чисел, а не другое действие?

Как и при решении задачи на сложение, рассмотренной нами выше, представим условие данной задачи наглядно, изобразив каждое дерево, посаженное около школы, кружком (рис. 3). Среди посаженных деревьев 3 березы — на рисунке выделим их, зачеркнув каждый кружок, изображающий березу. Тогда остальные деревья — рябины. Их столько, сколько будет, если из 8 вычесть 3, т.е.5 [52 ,С. 135].

Видим, что решение данной задачи тесно связано с выделением из данного множества подмножества и нахождением числа элементов в дополнении этого множества, т.е. вычитание чисел оказывается связанным с операцией дополнения подмножества.

Определение: Разностью целых неотрицательных чисел a и b называется число элементов в дополнении множества В до А при условии, что :

Часто, чтобы проверить правильность выполнения действия вычитания мы обращаемся к сложению. Почему? Очевидно потому, что существует связь между действиями вычитания и сложения. Пусть даны целые неотрицательные числа a и b, такие, что , и пусть разность этих чисел есть число элементов дополнения множества B до множества A, т.е.

Известно, что Следовательно, получаем, что

Отсюда мы получаем определение разности с точки зрения аксиоматической теории построения числа, которая описывалась выше.

Данное определение необходимо хорошо усвоить учащимся, так как проверка сложения вычитанием, а также вычитания сложением является одним из приемов самоконтроля, позволяющим избежать ошибок при вычислениях. Определение понятия вычитания как действия, обратного сложению, в явном виде не дается, но подчеркивается, что «вычитание связано со сложением: вычесть из числа 40 число 16 — значит найти такое число, которое при сложении его с числом 16 дает в сумме 40. Это число 24. Значит, 40-16 = 24».

Таким образом, в данном параграфе мы рассмотрели и раскрыли понятие сложения и вычитания с точки зрения аксиоматической теории и теоретико-множественного подхода. В начальном курсе математики первоначальное представление о действиях умножения и деления формируется с позиций теоретико-множественного подхода на основе практических упражнений через моделирование ситуаций на предметных совокупностях, но без введения соответствующей терминологии и символики.

Высшая арифметика исследует общие предложения о натуральных числах 1, 2, 3, . обычной арифметики. Высшая арифметика — дедуктивная наука, основанная на законах арифметики. Примерами таких предложений могут служить фундаментальная теорема о том, что каждое натураль­ное число разлагается на простые множители и это разложе­ние единственно, и теорема Лагранжа о том, что любое натуральное число представимо в виде суммы не более четы­рех точных квадратов.

Сложение. Любые два натуральных числа а и b имеют сумму, обозначаемую а+b, которая сама является натуральным числом.

Операция сложения удовлетворяет двум законам:

а + b = b + а (коммутативный закон сложения),

а + (b + с) = (а + b) + с (ассоциативный закон сложения),

скобки в последней формуле указывают порядок выполнения операций.

Умножение. Любые два натуральных числа а и b имеют про­изведение, обозначаемое а • b или ab, которое само является на­туральным числом.

Операция умножения удовлетворяет двум законам:

ab = bа (коммутативный закон умножения),

а(bс) = (аb)с (ассоциативный закон умножения).

Имеется также закон, связывающий сложение и умножение:

а(b + с) = ab + ас (дистрибутивный закон).

Простые числа. Очевидно, что каждое натуральное чис­ло а делится на 1 (отношение равно а) и на а (отношение равно 1). Множитель а, отличный от 1 или а, называется собственным множителем. Известно, что существуют числа, не имеющие соб­ственных множителей; они называются простыми числами. Первые несколько простых таковы:

2, 3, 5, 7, 11, 13, 17…

Число, не являющееся простым и не равное 1, называется со­ставным, такое число можно представить в виде произведения двух чисел, каждое из которых больше 1. Хорошо известно, что любое составное число можно представить в виде произведения простых; при этом, конечно, некоторые простые могут встре­титься по нескольку раз. Возьмем, например, число 666; ясно, что оно делится на 2, и мы получаем 666 = 2 • 333. Далее, 333 имеет очевидный множитель 3, откуда 333 = 3• 111. Множитель 111 снова делится на 3, так что 111 = 3 • 37. Следовательно,666 = 2 • 3 • 3 • 37,и мы получили представление составного числа 666 в виде про­изведения простых. Имеется общая теорема (основная теорема арифметики) о том, что каждое число представимо в виде произведения простых, или, что то же самое, любое число, большее 1, является простым либо разла­гается в произведение простых.

1. Аксиоматическая теория целых чисел. Свойства целых чисел. Построение модели

Об аксиоматическом способе построения теории. Определение натурального числа

При аксиоматическом построении какой-либо математической теории соблюдаются определенные правила:

· некоторые понятия теории выбираются в качестве основных и принимаются без определения;

· каждому понятию теории, которое не содержится в списке основных, дается определение;

· формулируются аксиомы – предложения, которые в данной теории принимаются без доказательства; в них раскрываются свойства основных понятий;

· каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано; такие предложения называют теоремами и доказывают их на основе аксиом и терем.

При аксиоматическом построении теории все утверждения выводятся из аксиом путем доказательства.

Поэтому к системе аксиом предъявляются особые требования:

· непротиворечивость (система аксиом называется непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг друга предложения);

· независимость (система аксиом называется независимой, если никакая из аксиом этой системы не является следствием других аксиом).

Множество, с заданным в нем отношением называется моделью данной системы аксиом, если в нем выполняются все аксиомы данной системы.

Построить систему аксиом для множества натуральных чисел можно многими способами. За основное понятие можно принять, например, сумму чисел или отношение порядка. В любом случае нужно задать систему аксиом, описывающие свойства основных понятий.

Дадим систему аксиом, приняв основное понятие операцию сложения.

Непустое множество N назовем множеством натуральных чисел, если в нем определена операция (a; b) → a + b, называемая сложением и обладающая свойствами:

1. сложение коммутативно, т.е. a + b = b + a.

2. сложение ассоциативно, т.е. (a + b) + c = a + (b + c).

3. для ,

4. в любом множестве А, являющемся подмножеством множества N, где А есть число а такое, что все хА, равны a + b, где bN.

Аксиом 1 – 4 достаточно, чтобы построить всю арифметику натуральных чисел. Но при таком построении уже нельзя опираться на свойства конечных множеств, не нашедших отражение в этих аксиомах.

Возьмем в качестве основного понятия отношение «непосредственно следовать за…», заданное на непустом множестве N. Тогда натуральным рядом чисел будет являться множество N, в котором определено отношение «непосредственно следовать за», а натуральными числами будут называться все элементы N, причем имеют место следующие аксиомы Пеано:

Во множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем называть его единицей, и обозначать символом 1.

Для каждого элемента а из N существует единственный элемент а, непосредственно следующий за а.

Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.

Всякое подмножество М множества N совпадает с N, если обладает свойствами: 1) 1 содержится в М; 2) из того, что а содержится в М, следует, что и а содержится в М.

Множество N, для элементов которого установлено отношение «непосредственно следовать за…», удовлетворяющее аксиомам 1 – 4, называется множеством натуральных чисел, а его элементы – натуральные числами.

Если в качестве множества N выбрать некоторое конкретное множество, на котором задано конкретное отношение «непосредственно следовать за…», удовлетворяющее аксиомам 1 – 4, то получим различные интерпретации (модели) данной системы аксиом.

Стандартной моделью системы аксиом Пеано является возникший в процессе исторического развития общества ряд чисел: 1, 2, 3, 4, 5, …

Моделью аксиом Пеано может быть любое счетное множество.

Например, I, II, III, IIII, …

один два три четыре, …

Рассмотрим последовательность множеств, в которой множество есть начальный элемент, а каждое последующее множество получается из предыдущего приписыванием еще одного кружка (рис.15).

Тогда N есть множество, состоящее из множеств описанного вида, и оно является моделью системы аксиом Пеано.

Действительно, во множестве N существует элемент , непосредственно не следующий ни за каким элементом данного множества, т.е. выполняется аксиома 1. Для каждого множества А рассматриваемой совокупности существует единственное множество, которое получается из А добавлением одного кружка, т.е. выполняется аксиома 2. Для каждого множества А существует не более одного множества, из которого образуется множество А добавлением одного кружка, т.е. выполняется аксиома 3. Если МN и известно, что множество А содержится в М, следует, что и множество, в котором на один кружок больше, чем в множестве А, также содержится в М, то М = N, и значит выполняется аксиома 4.

В определении натурального числа ни одну из аксиом опустить нельзя.

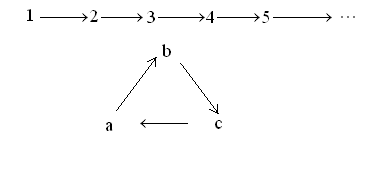
Установим, какие из множеств, приведенных на рис. 16, являются моделью аксиом Пеано.

Решение. На рисунке 16 а) изображено множество, в котором выполняются аксиомы 2 и 3. Действительно, для каждого элемента существует единственный, непосредственно следующий за ним, и существует единственный элемент, за которым он следует. Но в этом множестве не выполняется аксиома 1 (аксиома 4 не имеет смысла, т.к. в множестве нет элемента, непосредственно не следующего ни за каким другим). Поэтому данное множество не является моделью аксиом Пеано.

На рисунке 16 б) показано множество, в котором выполнены аксиомы 1, 3 и 4, но за элементом а непосредственно следуют два элемента, а не один, как требуется в аксиоме 2. Поэтому данное множество не является моделью аксиом Пеано.

На рис. 16 в) изображено множество, в котором выполнены аксиомы 1, 2, 4, но элемент с непосредственно следует сразу за двумя элементами. Поэтому данное множество не является моделью аксиом Пеано.

На рис. 16 г) изображено множество, удовлетворяющее аксиомам 2, 3, и, если в качестве начального элемента возьмем число 5, то данное множество будет удовлетворять аксиомам 1 и 4. Т.е., в данном множестве для каждого элемента существует единственный, непосредственно следующий за ним, и существует единственный элемент, за которым он следует. Существует и элемент, непосредственно не следующий ни за каким элементом этого множества, это 5, т.е. выполняется аксиома 1. Соответственно будет выполняться и аксиома 4. Поэтому данное множество является моделью аксиом Пеано.

Используя аксиомы Пеано, можно доказывать ряд утверждений Например, докажем, что для всех натуральных чисел выполняется неравенство х х.

Доказательство. Обозначим через А множество натуральных чисел, для которых а а. Число 1 принадлежит А, поскольку оно не следует ни за каким числом из N, а значит, не следует само за собой: 1 1. Пусть аА, тогда а а. Обозначим а через b. В силу аксиомы 3, аb, т.е. b bи bА.

Итак, множество А содержит 1 и вместе с каждым числом А содержит b = а. Значит, А = N. В силу определения А это означает, что для всех хА имеем неравенство х х.

1.2. Аксиоматическое определение натуральных чисел

При построении аксиоматической теории натуральных чисел первичными терминами будут являться «элемент» или «число» (которые в контексте данного пособия мы можем рассматривать как синонимы) и «множество», основными отношениями: «принадлежность» (элемент принадлежит множеству), «равенство» и «следовать за», обозначаемое а / (читается «число а штрих следует за числом а», например, за двойкой следует тройка, то есть 2 / = 3, за числом 10 следует число 11, то есть 10 / = 11 и т.д).

Множеством натуральных чисел (натуральным рядом, положительными целыми числами) называется множество N с введённым отношением «следовать за», в котором выполнены следующие 4 аксиомы:

А₁. Во множестве N существует элемент, называемый единицей, который не следует ни за каким другим числом.

А₂. Для каждого элемента натурального ряда существует единственный следующий за ним.

А₃. Каждый элемент N следует не более чем за одним элементом натурального ряда.

А₄.(Аксиома индукции) Ели подмножество М множества N содержит в себе единицу, а также вместе с каждым своим элементом а содержит и следующий за ним элемент а / , то М совпадает N.

Те же аксиомы можно записать кратко с помощью математических символов:

А₁ ( 1  N) ( a  N) a / ≠ 1

A₂ ( a  N) ( a /  N) a = b => a / = b /

A₃ a / = b / => a = b

=> М = N

Если элемент b следует за элементом а (b = а / ), то будем говорить, что элемент а является предшествующим для элемента b (или предшествует b). Данная система аксиом носит название системы аксиом Пеано (так как была введена в XIX веке итальянским математиком Джузеппе Пеано). Это лишь один из возможных наборов аксиом, позволяющий определить множество натуральных чисел; существуют и другие эквивалентные подходы.

Простейшие свойства натуральных чисел

Свойство 1. Если элементы различны, то и следующие за ними различны, то есть

Доказательство осуществляется методом от противного: предположим, что a / = b / , тогда (по А₃) a = b, что противоречит условию теоремы.

Свойство 2. Если элементы различны, то и предшествующие им (если они существуют) различны, то есть

Доказательство: предположим, что a = b, тогда, согласно А₂ имеем a / = b / , что противоречит условию теоремы.

Свойство 3. Никакое натуральное число не равно следующему за ним.

Доказательство: Введём в рассмотрение множество М, состоящее из таких натуральных чисел, для которых данное условие выполняется

Доказательство будем проводить, опираясь на аксиому индукции. По определению множества М, оно является подмножеством множества натуральных чисел. Далее 1М, так как единица не следует ни за каким натуральным числом (А₁), а значит в том числе и для а = 1 имеем: 1  1 / . Предположим теперь, что некоторое а  М. Это означает, что a  a / (по определению М), откуда a /  (a / ) / (свойство 1), то есть a /  М. Из всего выше сказанного на основании аксиомы индукции можно заключить, что М = N, то есть наша теорема верна для всех натуральных чисел.

Теорема 4. Для любого натурального числа отличного от 1 существует предшествующее ему число.

Доказательство: Рассмотрим множество

Данное М есть подмножество множества натуральных чисел, единица явно принадлежит данному множеству. Вторая же часть этого множества – это элементы, для которых существуют предшествующие, следовательно, если а  М, то a / тоже принадлежит М (его второй части, так как у a / есть предшествующий – это а). Таким образом, на основании аксиомы индукции М совпадает с множеством всех натуральных чисел, а значит все натуральные числа это либо 1, либо те, для которых существует предшествующий элемент. Теорема доказана.

Непротиворечивость аксиоматической теории натуральных чисел

В качестве интуитивной модели множества натуральных чисел можно рассматривать наборы чёрточек: числу 1 будет соответствовать |, числу 2 ||, и т.д., то есть натуральный ряд будет иметь вид:

Данные ряды чёрточек могут служить моделью натуральных чисел, если в качестве отношения «следовать за» использовать «приписывание одной чёрточки к числу». Справедливость всех аксиом является интуитивно очевидной. Разумеется, данная модель не является строго логической. Для построения строгой модели нужно иметь другую заведомо непротиворечивую аксиоматическую теорию. Но такой теории в нашем распоряжении, как уже отмечалось выше, нет. Таким образом, либо мы вынуждены опереться на интуицию, либо не прибегать к методу моделей, а сослаться на то, что на протяжении более чем 6 тысячелетий, во время которых осуществляется изучение натуральных чисел, никаких противоречий с данными аксиомами обнаружено не было.

Независимость системы аксиом Пеано

Для доказательства независимости первой аксиомы достаточно построить модель, в которой аксиома А₁ ложна, а аксиомы А₂, А₃, А₄ истины. Рассмотрим в качестве первичных терминов (элементов) числа 1, 2, 3, а отношение «следовать за» определим соотношениями: 1 / = 2, 2 / = 3, 3 / = 1.

В этой модели нет элемента, который бы не следовал ни за каким другим (аксиома 1 ложна), но все остальные аксиомы выполняются. Таким образом, первая аксиома не зависит от остальных.

Вторая аксиома состоит из двух частей – существования и единственности. Независимость данной аксиомы (в части существования) можно проиллюстрировать на модели из двух чисел с отношением «следовать за», заданным единственным соотношением: 1 / = 2:

Для двойки отсутствует следующий элемент, аксиомы же А₁, А₃, А₄ истинны.

Независимость данной аксиомы, в части единственности, иллюстрирует модель, в которой множеством N будет множество всех обычных натуральных чисел, а также всевозможных слов (наборов букв, не обязательно имеющих смысл), составленных из букв латинского алфавита (после буквы z следующей будет аа, затем аb … аz, затем ba …; за всеми возможными словами из двух букв, последним из которых будет zz, последует слово ааа, и так далее). Отношение «следовать за» введём так, как показано на рисунке:

Здесь аксиомы А₁, А₃, А₄ также истинны, но за 1 следует сразу два элемента 2 и а. Таким образом, аксиома 2 не зависит от остальных.

Независимость аксиомы 3 иллюстрирует модель:

в которой А₁, А₂, А₄ истинны, но число 2 следует и за числом 4, и за числом 1.

Для доказательства независимости аксиомы индукции используем множество N, состоящее из всех натуральных чисел, а также трёх букв . Отношение следования в данной модели можно ввести так, как показано на следующем рисунке:

Здесь для натуральных чисел используется обычное отношение следования, а для букв отношение «следовать за» определяется следующими формулами: a / = b, b / = c, c / = a. Очевидно, что 1 не следует ни за каким натуральным числом, для каждого имеется следующий, и притом только один, каждый элемент следует не более чем за одним элементом. Однако если мы рассмотрим множество М состоящее из обычных натуральных чисел, то это будет подмножество данного множества, содержащее единицу, а также следующий элемент для каждого элемента из М. Однако это подмножество не будет совпадать со всей рассматриваемой моделью, так как не будет содержать в себе буквы a, b, c. Таким образом, аксиома индукции в данной модели не выполняется, а, следовательно, аксиома индукции не зависит от остальных аксиом.

Аксиоматическая теория натуральных чисел является категоричной (полной в узком смысле).

Для доказательства категоричности достаточно ввести изоморфизм для любых двух моделей натуральных чисел. Такой изоморфизм можно построить для натуральных чисел исходя из условий:

Принцип полной математической индукции.

Теорема индукции. Пусть некоторое утверждение Р(n) сформулировано для всех натуральных чисел, и пусть а) Р(1) – истинно, б) из того, что Р(k) истинно, следует, что Р(k / ) также истинно. Тогда утверждение Р(n) справедливо для всех натуральных чисел.

Для доказательства введём множество М таких натуральных чисел n (М  N), для которых утверждение Р(n) истинно. Воспользуемся аксиомой A₄, то есть попытаемся доказать, что:

Если нам это удастся, то, согласно аксиоме А₄, мы сможем сделать вывод, что M = N, то есть P(n) истинно для всех натуральных числе.

1) По условию а) теоремы, Р(1) истинно, следовательно, 1  М.

2) Если некоторое k  М, то (по построению М) Р(k) – истинно. По условию б) теоремы, это влечёт за собой истинность Р(k / ), а значит k /  М.

Таким образом, по аксиоме индукции (А₄) М = N, а значит Р(n) истинно для всех натуральных чисел.

Таким образом, аксиома индукции позволяет создать метод доказательства теорем «по индукции». Данный метод играет ключевую роль при доказательстве основных теорем арифметики, касающихся натуральных чисел. Он состоит в следующем:

1) проверяется справедливость утверждения для n=1 (база индукции),

2) предполагается справедливость этого утверждения для n=k, где k – произвольное натуральное число (индукционное предположение), и с учётом этого предположения устанавливается справедливость утверждения для n=k / (индукционный шаг).

Доказательство, основанное на данном алгоритме, называется доказательством методом математической индукции.

Задания для самостоятельного решения

№ 1.1. Выяснить, какие из перечисленных систем удовлетворяют аксиомам Пеано (являются моделями множества натуральных чисел), определить, какие аксиомы выполнены, а какие – нет.

д) нечётные натуральные числа, n / = n +1;

е) нечётные натуральные числа, n / = n +2;

ж) Натуральные числа с отношением n / = n + 2;

з) N =, 1 / = 3, 2 / = 3, 3 / = 2;

и) N =, 1 / = 2, 2 / = 3, 3 / = 4, 4 / = 5, 5 / = 1;

к) Натуральные числа, кратные 3 с отношением n / = n + 3

л) Чётные натуральные числа с отношением n / = n + 2

м) Целые числа, .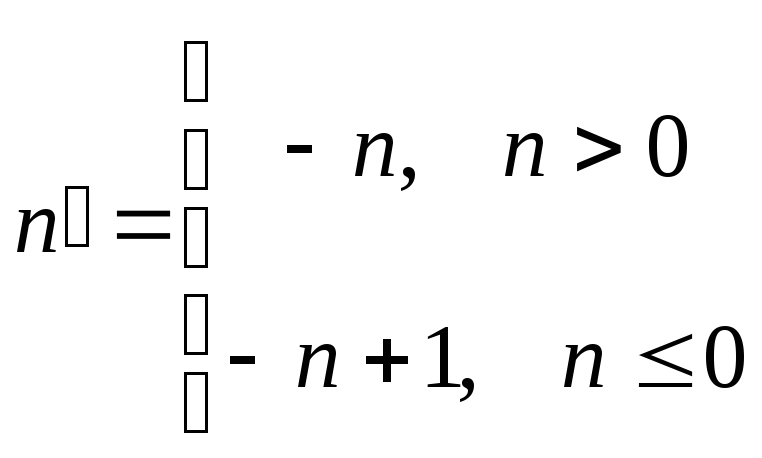

Лекция 1. Аксиоматическое построение системы натуральных чисел

Аксиоматический метод в математике.

Основные понятия и отношения аксиоматической теории натурального ряда. Определение натурального числа.

Сложение натуральных чисел.

Умножение натуральных чисел.

Свойства множества натуральных чисел

Вычитание и деление натуральных чисел.

Аксиоматический метод в математике

При аксиоматическом построении какой-либо математической теории соблюдаются определенные правила:

1. Некоторые понятия теории выбираются в качестве основных и принимаются без определения.

2. Формулируются аксиомы, которые в данной теории принимаются без доказательства, в них раскрываются свойства основных понятий.

3. Каждому понятию теории, которое не содержится в списке основных, даётся определение, в нём разъясняется его смысл с помощью основных и предшествующих данному понятию.

4. Каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано. Такие предложения называют теоремами и доказывают их на основе аксиом и теорем, предшествующих рассматриваемой.

Система аксиом должна быть :

а) непротиворечивой:мы должны быть уверены,что, делая всевозможные выводы из данной системы аксиом, никогда не придем к противоречию;

б) независимой: никакая аксиома не должна быть следствием других аксиом этой системы.

в) полной, если в ее рамках всегда можно доказать или данное утверждение, или его отрицание.

Первым опытом аксиоматического построения теории можно считать изложение геометрии Евклидом в его «Началах»(3 в. до н.э.). Значительный вклад в развитие аксиоматического метода построения геометрии и алгебры внесли Н.И. Лобачевский и Э.Галуа. В конце 19 в. итальянским математиком Пеано была разработана система аксиом для арифметики.

Основные понятия и отношения аксиоматической теории натурального числа. Определение натурального числа.

В качестве основного(неопределяемого) понятия в некотором множестве N выбирается отношение «непосредственно следовать за», а также используются теоретико-множественные понятия, а также правила логики.

Элемент, непосредственно следующий за элементом а, обозначают а’.

Отношения «непосредственно следовать за» удовлетворяет следующим аксиомам:

Аксиомы Пеано:

Аксиома 1. В множестве Nсуществует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем называть его единицей и обозначать символом 1.

Аксиома 2. Для каждого элемента аиз Nсуществует единственный элемент а’, непосредственно следующий за а.

Аксиома 3. Для каждого элемента аиз N существует не более одного элемента, за которым непосредственно следует а.

Аксиома 4. Всякое подмножество Ммножества Nсовпадает с N, если обладает свойствами: 1) 1 содержится в М; 2) из того, что асодержится в М, следует, что и а’содержится в М.

Определение 1. Множество N, для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам 1-4, называется множеством натуральных чисел, а его элементы — натуральными числами.

В данном определении ничего не говорится о природе элементов множества N. Значит, она может быть какой угодно. Выбирая в качестве множества N некоторое конкретное множество, на котором задано конкретное отношение «непосредственно следовать за», удовлетворяющее аксиомам 1-4, мы получим модель данной системы аксиом.

Стандартной моделью системы аксиом Пеано является возникший в процессе исторического развития общества ряд чисел: 1,2,3,4. Натуральный ряд начинается с числа 1 (аксиома 1); за каждым натуральным числом непосредственно следует единственное натуральное число (аксиома 2); каждое натуральное число непосредственно следует не более чем за одним натуральным числом (аксиома 3); начиная от числа 1 и переходя по порядку к непосредственно следующим друг за другом натуральным числам, получаем все множество этих чисел (аксиома 4).

Итак, мы начали аксиоматическое построение системы натуральных чисел с выбора основного отношения «непосредственно следовать за» и аксиом, в которых описаны его свойства. Дальнейшее построение теории предполагает рассмотрение известных свойств натуральных чисел и операций над ними. Они должны быть раскрыты в определениях и теоремах, т.е. выведены чисто логическим путем из отношения «непосредственно следовать за», и аксиом 1-4.

Первое понятие, которое мы введем после определения натурального числа, — это отношение «непосредственно предшествует», которое часто используют при рассмотрении свойств натурального ряда.

Определение 2. Если натуральное число bнепосредственно следует за натуральным числом а, то число а называется непосредственно предшествующим (или предшествующим) числу b .

Отношение «предшествует» обладает рядом свойств.

Теорема 1. Единица не имеет предшествующего натурального числа.

Теорема 2. Каждое натуральное число а, отличное от 1, имеет единственное предшествующее число b , такое, что b’ = а.

Аксиоматическое построение теории натуральных чисел не рас­сматривается ни в начальной, ни в средней школе. Однако те свойства отношения «непосредственно следовать за», которые нашли отражение в аксиомах Пеано, являются предметом изучения в начальном курсе математики. Уже в первом классе при рассмотрении чисел первого десятка выясняется, как может быть получено каждое число. При этом используются понятия «следует» и «предшествует». Каждое новое число выступает как продолжение изученного отрезка натурального ряда чисел. Учащиеся убеждаются в том, что за каждым числом идет следующее, и притом только одно, что натуральный ряд чисел бесконечен.

Сложение натуральных чисел

По правилам построения аксиоматической теории, определение сложения натуральных чисел нужно ввести, используя только отно­шение «непосредственно следовать за», и понятия «натуральное чис­ло» и «предшествующее число».

Предварим определение сложения следующими рассуждениями. Если к любому натуральному числу а прибавить 1, то получим число а’, непосредственно следующее за а, т.е. а + 1 = а’ и, следовательно, мы получим правило прибавления 1 к любому натуральному числу. Но как прибавлять к числу а натуральное число b, отличное от 1? Воспользуемся следующим фактом: если известно, что 2 + 3 = 5, то сумма 2 + 4 = 6, которое непосредственно следует за числом 5. Происходит так потому, что в сумме 2 + 4 второе слагаемое есть число, непосредственно следующее за числом 3. Таким образом, 2 + 4 =2+3‘ =(2+3)’. В общем виде имеем, .

Эти факты положены в основу определения сложения натуральных чисел в аксиоматической теории.

Определение 3. Сложениемнатуральных чисел называется алгеб­раическая операция, обладающая свойствами:

1) ;

2)

Число а + bназывается суммой чисел а и b , а сами числа аиb— слагаемыми.

Аксиоматическая теория натуральных чисел

ГОУВПО

Тульский государственный педагогический университет

Имени Л.Н.Толстого

ЧИСЛОВЫЕ СИСТЕМЫ

Тула 2008

Числовые системы

Пособие предназначено для студентов математических специальностей педагогического вуза и разработано в соответствии с госстандартом по курсу «Числовые системы». Изложен теоретический материал. Разобраны решения типовых заданий. Приведены упражнения для решения на практических занятиях.

кандидат физико-математических наук, доцент кафедры алгебры и геометрии ТГПУ им. Л. Н. Толстого Ю. А. Игнатов

кандидат физико-математических наук, профессор кафедры математического анализа ТГПУ им. Л. Н. Толстого И. В. Денисов

Учебное издание

Числовые системы

ИГНАТОВ Юрий Александрович

© Ю. Игнатов, 2008 г.

ЧИСЛОВЫЕ СИСТЕМЫ

Настоящий курс относится к основаниям математики. В нем дается строгое аксиоматическое построение основных числовых систем: натуральных, целых, рациональных, действительных, комплексных, а также кватернионов. В основе лежит теория формальных аксиоматических систем, рассмотренная в курсе математической логики.

В каждом пункте нумерация теорем ведется сначала. При необходимости ссылки на теорему из другого пункта используется ступенчатая нумерация: перед номером теоремы ставится номер пункта. Например, теорема 1.2.3 – это теорема 3 из пункта 1.2.

Натуральные числа

Аксиоматическая теория натуральных чисел

Аксиоматическуя теорию определяют следующие элементы:

— набор функциональных символов для обозначения операций;

— набор предикатных символов для обозначения отношений;

— список аксиом, связывающих указанные выше элементы.

Для формальной аксиоматической теории указываются еще правила вывода, с помощью которых доказываются теоремы. При этом все утверждения записываются в виде формул, смысл которых не имеет значения, и над этими формулами производятся преобразования по заданным правилам. В содержательной аксиоматической теории правила вывода не указываются. Доказательства проводятся на основе обычных логических построений, учитывающих смысл доказываемых утверждений.

В настоящем курсе строятся содержательные теории основных числовых систем.

Важнейшее требование к аксиоматической теории – ее непротиворечивость. Доказательство непротиворечивости осуществляется построением модели теории в другой теории. Тогда непротиворечивость рассматриваемой теории сводится к непротиворечивости той теории, в которой построена модель.

Для системы целых чисел модель строится в рамках системы натуральных чисел, для рациональных – в системе целых чисел, и т.д. Получается цепочка аксиоматических теорий, в которой каждая теория опирается на предшествующую. Но для первой теории в этой цепочке, а именно теории натуральных чисел, модель строить негде. Поэтому для системы натуральных чисел следует построить такую теорию, для которой существование модели не вызывает сомнений, хотя строго это доказать невозможно.

Теория должна быть очень простой. С этой целью мы рассматриваем систему натуральных чисел только как инструмент для счета предметов. Операции сложения, умножения, отношение порядка должны быть определены после того, как теория в указанном виде будет построена.

Для нужд счета система натуральных чисел должна представлять собой последовательность, в которой определен первый элемент (единица) и для каждого элемента определен следующий за ним. В соответствии с этим получаем следующую теорию.

Константа: 1 (единица).

Функциональный символ: «¢». Обозначает унарную операцию «следовать за», то есть а¢ – число, следующее за а. При этом число а называется предшествующим для а¢.

Специальных предикатных символов нет. Используются обычное отношение равенства и теоретико-множественные отношения. Аксиомы для них указываться не будут.

Множество, на котором строится теория, обозначается N.

(N1) («a) a¢ ¹ 1 (единица не следует ни за каким числом).

(N2) («a)(«b) (a¢ = b¢ ® a = b) (у каждого числа есть не более одного предшествующего).

(N3) M Í N, 1Î M, («a)(aÎM ® a¢Î M) Þ M = N (аксиома математической индукции).

Приведенная аксиоматика была предложена (с незначительными изменениями) итальянским математиком Пеано в конце XIX века.

Из аксиом нетрудно вывести некоторые теоремы.

Теорема 1. (Метод математической индукции). Пусть Р(n) – предикат, определенный на множестве N. Пусть истинно Р(1) и («n)(P(n)®P(n¢)). Тогда Р(n) – тождественно истинный предикат на N.

Доказательство. Пусть М – множество натуральных чисел n, для которых Р(n) истинно. Тогда 1ÎM по условию теоремы. Далее, если nÎM, то P(n) истиннопо определению М, P(n¢) истинно по условию теоремы, и n¢ÎM по определению М. Выполняются все посылки аксиомы индукции, следовательно, M = N. Согласно определению М, это значит, что Р(n) истинно для всех чисел из N. Теорема доказана.

Теорема 2. Любое число а ¹ 1 имеет предшествующее, и притом только одно.

Доказательство. Пусть М – множество натуральных чисел, содержащее 1 и все числа, имеющие предшествующее. Тогда 1ÎM. Если aÎM, то a¢Î M, так как a¢ имеет предшествующее (здесь даже не используется условие aÎM). Значит, по аксиоме индукции M = N. Теорема доказана.

Теорема 3. Любое число отлично от следующего за ним.

Доказательство – в качестве упражнения.

Упражнение. Определив натуральные числа 1¢ = 2, 2¢ = 3, 3¢ = 4, 4¢ = 5, 5¢ = 6, докажите, что 2 ¹ 6.

Сложение натуральных чисел

Для сложения натуральных чисел дается следующее рекурсивное определение.

Определение.Сложением натуральных чисел называется бинарная операция, которая натуральным числам а и b ставит в соответствие число a + b, обладающая свойствами:

Требуется доказать, что это определение корректно, то есть операция, удовлетворяющая заданным свойствам, существует. Эта задача кажется очень простой: достаточно провести индукцию по b, считая а фиксированным. При этом требуется выделить множество М значений b, для которых операция a + b определена и удовлетворяет условиям (S1) и (S2). Выполняя индуктивный переход, мы должны предположить, что для b операция выполняется, и доказать, что она выполняется для b¢. Но в свойстве (S2), которое должно выполняться для b, уже есть ссылка на a + b¢. Значит, это свойство автоматически предполагает существование операции и для a + b¢, а значит, и для последующих чисел: ведь для a + b¢ тоже должно выполняться свойство (S2). Можно подумать, что это только облегчает задачу, делая индуктивный переход тривиальным: доказываемое утверждение просто повторяет индуктивное предположение. Но сложность здесь в доказательстве для базы индукции. Для значения b = 1 тоже должны выполняться свойства (S1) и (S2). Но свойство (S2), как показано, предполагает существование операции для всех значений, следующих за 1. Значит, проверка базы индукции предполагает доказательство не для единицы, а для всех чисел, и индукция теряет смысл: база индукции совпадает с доказываемым утверждением.

Приведенное рассуждение не означает, что рекурсивные определения некорректны или требуют каждый раз тщательного обоснования. Для их обоснования нужно использовать свойства натуральных чисел, которые на данном этапе только устанавливаются. Когда они будут установлены, можно будет доказать законность рекурсивных определений. Пока же докажем существование сложения индукцией по а: в формулах (S1) и (S2) нет связи между сложением для а и а¢.

Теорема 1. Сложение натуральных чисел всегда выполнимо, причем однозначно.

Доказательство. а) Сначала докажем единственность. Зафиксируем а. Тогда результат операции a + b есть функция от b. Предположим, что есть две такие функции f(b) и g(b), обладающие свойствами (S1) и (S2). Докажем, что они равны.

значит, b¢ÎМ. По аксиоме индукции M = N. Единственность доказана.

б) Теперь индукцией по а докажем существование операции a + b. Пусть М – множество тех значений а, для которых операция a + b со свойствами (S1) и (S2) определена для всех b.

Пусть а = 1. Приведем пример такой операции. Полагаем по определению 1 + b = = b¢. Покажем, что для этой операции выполняются свойства (S1) и (S2). (S1) имеет вид 1 + 1 = 1¢, что соответствует определению. Проверяем (S2): 1+ b¢ =(b¢)¢ =
= (1+ b)¢, и (S2) выполняется. Значит, 1ÎМ.

Пусть теперь аÎМ. Докажем, что а¢ÎМ. Полагаем по определению
a¢+ b = (a+ b)¢. Тогда

и свойства (S1) и (S2) выполняются.

Таким образом, M = N, и сложение определено для всех натуральных чисел. Теорема доказана.

Теорема 2. Сложение натуральных чисел ассоциативно, то есть

Доказательство. Зафиксируем а и b и проведем индукцию по с. Пусть М – множество тех чисел с, для которых равенство справедливо. Имеем по свойствам (S1) и (S2):

Пусть теперь сÎM. Тогда

и c¢ÎМ. По аксиоме (N3) М = N. Теорема доказана.

Теорема 3. Сложение натуральных чисел коммутативно, то есть

Доказательство. Зафиксируем а и проведем индукцию по b.

Пусть b = 1, то есть требуется доказать равенство

Это равенство доказываем индукцией по а.

При а = 1 равенство тривиально. Пусть оно выполняется для а, докажем его для а¢. Имеем

Индуктивный переход завершен. По принципу математической индукции равенство (2) верно для всех а. Тем самым доказано утверждение базы индукции по b.

Пусть теперь формула (1) выполняется для b. Докажем ее для b¢. Имеем

По принципу математической индукции теорема доказана.

Теорема 4. a + b ¹ b.

Доказательство – в качестве упражнения.

Теорема 5. Для любых чисел а и b имеет место один и только один из случаев:

2) Существует число k такое, что a = b + k.

3) Существует число l такое, что b = a + l.

Доказательство. Из теоремы 4 следует, что имеет место не более чем один из этих случаев, так как, очевидно, слу­чаи 1) и 2), а также 1) и 3) не могут иметь место одновременно. Если бы одновременно имели место случаи 2) и 3), то a = b + k =
= (а + l) + k = а + (l + k), что снова противоречит тео­реме 4. Докажем, что хотя бы один из этих случаев всегда имеет место.

Пусть выбрано число а и М – множество тех b, для каждого из которых при данном a имеет место случай 1), 2) или 3).

Пусть b = 1. Если a = 1, то имеем случай 1). Если а ¹ 1,то по теореме 1.1.2 имеем

то есть имеем случай 2) для b = 1. Значит, 1 принадлежит М.

Пусть b принадлежит М. Тогда возможны случаи:

— а = b, значит, b’ = b + 1 = а + 1, то есть имеем случай 3)для b’;

— а = b + k, и если k = 1, то а = b + 1 = b’, то есть имеет место случай 1) для b’;

если же k ¹ 1, то k = т’ и

то есть имеет место случай 2) для b’;

Во всех случаях b’ принадлежит М. Тео­рема доказана.

Упражнение. Докажите на основании определения суммы, что 1 + 1 = 2, 1 + 2 = 3, 2 + 2 = 4, 2 + 3 = 5, 2 + 4 = 3 + 3 = 6.

Умножение натуральных чисел

Определение.Умножением натуральных чисел называется бинарная операция, которая натуральным числам а и b ставит в соответствие число ab (или a×b), обладающая свойствами:

(P2) аb’ = ab + а для любых а и b.

Относительно определения умножения сохраняют силу все замечания, которые были сделаны в предыдущем пункте по поводу определения сложения. В частности, из него еще неясно, что соответствие с данными в определении свойствами существует. Поэтому большое принципиальное значение имеет следующая теорема, аналогичная теореме 1.2.1.

Теорема 1. Умножение натуральных чисел существует и притом только одно. Иными словами, умножение всегда выпол­нимо и однозначно.

Доказательство вполне аналогично доказательству теоремы 1.2.1 и предлагается в качестве упражнения.

Легко доказываются свойства умножения, сформулированные в следующих теоремах. Доказательство каждой теоремы опирается на предыдущие.

Теорема 2. (Правый закон дистрибутивности): (a + b)c = ac + bc.

Теорема 3. Умножение коммутативно: ab = ba.

Теорема 4. (Левый закон дистрибутивности): c(a + b) = сa + сb.

Теорема 5. Умножение ассоциативно: a(bc) = (ab)c.

Определение.Полукольцом называется система , где + и × – бинарные операции сложения и умножения, удовлетворяющие аксиомам:

(1) – коммутативная полугруппа, то есть сложение коммутативно и ассоциативно;

(2) – полугруппа, то есть умножение ассоциативно;

(3) выполняется правая и левая дистрибутивность.

С алгебраической точки зрения система натуральных чисел относительно сложения и умножения образует полукольцо.

Упражнение. Докажите на основании определения произведения, что
2×2 = 4, 2×3 = 6.

Упражнения

Докажите тождества:

1.1 2 + 2 2 + . + n 2 = .

2.1 3 + 2 3 + . + n3 = .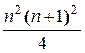

Найдите сумму:

3. .

4. .

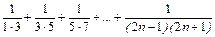
5. .

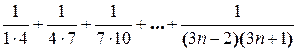
6.1×1! + 2×2! + . + n×n!.

Докажите неравенства:

7.n 2 4.

8.2 n n ³ 1 + nx, где x > –1.

10. при n > 1.

11. при n > 1.

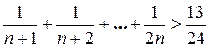
12. .

13.Найдите ошибку в доказательстве по индукции, что все числа равны между собой. Доказываем равносильное утверждение: в любом множестве из n чисел все числа равны между собой. При n = 1 утверждение верно. Пусть оно верно для n = k, докажем его для n = k + 1. Возьмем множество из произвольных
(k + 1) чисел. Удалим из него одно число а. Осталось k чисел, по индуктивному предположению они равны между собой. В частности, равны два числа b и с. Теперь удалим из множества число с и включим а. В получившемся множестве по-прежнему k чисел, значит, они тоже равны между собой. В частности, a = b. Значит, a = b = c, и все (k + 1) числа равны между собой. Индуктивный переход завершен, и утверждение доказано.

14.Докажите усиленный принцип математической индукции:

Пусть A(n) – предикат на множестве натуральных чисел. Пусть А(1) истинен и из истинности A(k) для всех чисел k , определяемое условием

есть отношение строгого линейного порядка.

8.Пусть áМ, fñ – линейно упорядоченное множество. Докажите, что отношение ³, определяемое условием

есть отношение нестрогого линейного порядка.

Определение.Линейно упорядоченное множество áМ, fñ, в котором каждое непустое подмножество имеет наименьший элемент, называется вполне упорядоченным. Отношение f в этом случае называется отношением полного порядка.

Согласно теореме 1.4.6, система натуральных чисел – вполне упорядоченное множество.

Определение.Пусть áМ, fñ – вполне упорядоченное множество. Интервалом, отделенным элементом а, называется множество Р_а всех элементов, лежащих ниже а и отличных от а, то есть

В частности, если а – минимальный элемент, то Р_а = Æ.

Теорема 1. (Принцип трансфинитной индукции). Пусть áМ, fñ – вполне упорядоченное множество и А Í М. Пусть для каждого элемента а из М из принадлежности к А всех элементов интервала Р_а следует, что а Î А. Тогда А = М.

Пусть А’ = М \ А есть теоретико-множест­венная разность множеств М и А. Если А’ = Æ, то А = М, и утверждение теоремы выполняется. Если А’ ¹ Æ, то, так как М – вполне упорядоченное множество, то множество А’ содержит наименьший элемент т. В таком случае, все элементы, предшествующие т и отличные от т, не принадлежат А’ и, значит, принадлежат А. Таким образом, Р_m Í А. Поэтому по условию теоремы т Î А, и, следо­вательно, т Ï А’, в противоречие с предположением.

Пусть áА; fñ – упорядоченное множест­во. Мы будем предполагать, что А – конечное множество. С каж­дым элементом а множества А сопоставим какую-нибудь точку Т (а) данной плоскости так, что если элемент а непосредственно следует за элементом b, то точку Т (a) будем располагать выше точ­ки Т (b) и соединять их отрезком. В результате мы получим граф, отвечающий данному упорядоченному множеству.

Упражнения

10.Пусть áМ, f₁ñ и áL, f₂ñ – вполне упорядо­ченные множества такие, что
M Ç L = Æ. Во множестве M È L определим бинарное отношение f следующими условиями:

Докажите, что система áМÈL, fñ – вполне упорядоченное множество.

Упорядоченные полугруппы

Определение.Полугруппой называется алгебра áА, *ñ, где * – ассоциативная бинарная операция.

Определение.Полугруппа áА, *ñ называется полугруппой с сокращением, если в ней выполняются свойства

Определение.Упорядоченной полугруппой называется си­стема áА, +, fñ, где:

1) система áА, +ñ – полугруппа;

2) система áА, fñ – упорядоченное множество;

3) отношение f монотонно относительно полугрупповой операции, то есть
a f b Þ a + c f b + c, c + a f c + b.

Упорядоченную полугруппу áА, +, fñ называют упорядочен­ной группой, если система áА, +ñ – группа.

В соответствии с видами отношения порядка определяются линейно упорядоченная полугруппа, линейно упорядоченная группа, частично упоря­доченная полугруппа, строго упорядоченная полугруппа и т. д.

Теорема 1. В упорядоченной полугруппе áА, +, fñ неравенства можно складывать, то есть a f b, c f d Þ a + c f b + d.

откуда по транзитивности a + c f b + d. Теорема доказана.

Упражнение 1. Докажите, что система натуральных чисел – частично упорядоченная полугруппа относительно умножения и отношения делимости.

Легко видеть, что система áN, +, >ñ – строго упорядоченная полугруппа, áN, +, ³ñ – нестрого упорядоченная полугруппа. Можно привести пример такого упорядочивания полугруппы áN, +ñ, в которой порядок не является ни строгим, ни нестрогим.

Упражнение 2. Определим порядок f в системе натуральных чисел следующим образом: a f b Û a ³ b & a ¹ 1. Докажите, что áN, +, fñ – упорядоченная полугруппа, в которой порядок не является ни строгим, ни нестрогим.

Пример 1.Пусть А – множество натуральных, чисел, не равных единице. Определим отношение f в А следующим образом:

Доказать, что система áА, +, fñ – частично и строго упорядоченная полугруппа.

Доказательство. Проверим транзитивность:

a f b, b f c Þ a = b + k, b ¹ 3, b = c + l, c ¹ 3 Þ a = c + (k + l), c ¹ 3 Þ a f c.

Так как a f b Þ a > b, то выполняется антирефлексивность. Из упражнения 2.1.1 следует, что f – отношение строгого порядка. Порядок частичный, так как элементы 3 и 4 не находятся ни в каком отношении.

Монотонность отношения f относительно сложения выполняется. Действительно, условие a f b Þ a + c f b + c могло бы нарушиться, только когда
b + c = 3. Но сумма может быть равна 3, так как в можестве А нет единицы.

Группу из двух элементов линейно и строго упорядочить нельзя. В самом деле, пусть 0 и 1 – ее элементы (0 – нуль группы). Предположим, что 1 > 0. Тогда получим 0 = 1 + 1 > 0 + 1 = 1.

Теорема 2. Всякую линейно упорядоченную по­лугруппу с сокращением можно линейно и строго упорядочить.

Доказательство. Пусть áА, +, fñ – упорядоченная полугруппа. Отношение строгого порядка > определяется, как в упражнении 2.1.5: a > b Û a f b & a ¹ b. Покажем, что выполняется условие 3) из определения упорядоченной полугруппы.

Если a + c = b + c то, сокращая, получим a = b, что противоречит условию
а > b. Значит, a + c ¹ b + c, и a + c > b + c. Аналогично проверяется вторая часть условия 3), что доказывает теорему.

Теорема 3. Если áА, +, fñ – линейно и строго упорядо­ченная полугруппа, то:

Доказательство. Пусть а + с = b + с. Если a ¹ b, то в силу связности а f b или
b f a. Но тогда соответственно а + с f b+ с или b + с f a+ с, что противоречит условию а + с = b + с. Аналогично разбираются другие случаи.

Итак, всякая линейно и строго упорядоченная полугруппа – полугруппа с сокращением.

Определение.Пусть áА, +, fñ – упорядоченная полу­группа. Элемент а множества А называют положительным (отри­цательным), если а + а ¹ а и a + a f а (соответственно а f а + а).

Пример 2.Доказать, что элемент упорядоченной коммутативной полугруппы с сокращением, больший положительного элемента, не обязательно положителен.

Решение. Воспользуемся примером 1. Имеем 2 + 2 f 2, значит, 2 – положительный элемент. 3 = 2 + 1, значит, 3 f 2. В то же время соотношение 3 + 3 f 3 не выполняется, значит, 3 не является положительным элементом.

Теорема 4. Сумма положительных элементов коммута­тивной полугруппы с сокращением положительна.

Доказательство. Если а + а f а и b + b f b, то по теореме 1

Остается проверить, что (а + b)+ (a + b)¹ а + b. Имеем:

b + b f b Þ a + b + b f a + b (1)

Предположим, что (а + b)+ (a + b)= а + b. Подставив в (1), получаем

a + b + b f a + b + a + b Þ a f a + a.

В силу антисимметричности а = а + а. Это противоречит тому, что элемент а положительный.

Теорема 5. Если а – положительный элемент линейно и строго упорядоченной полугруппы, то для любого b имеем a + b f b, b + a f b.

Доказательство. Имеем а+ а fа Þ а+ а+ b f а+ b. Если неверно, что a+ b f b, то в силу линейности выполняется a + b = b или b f a+ b. Прибавляя слева а, получаем соответственно а+ а+ b = а+ b или а+ b f а+ а + b. Эти условия противоречат антисимметричности и строгости отношения порядка.

Теорема 6. Пусть áА, +, fñ – линейно и строго упорядо­ченная полугруппа, аÎА и а + а ¹ a. Тогда элементы:

все различны. Если при этом система áА, +, fñ – группа, то различны и все элементы:

(под k*a, kÎ N, aÎA, понимается сумма а+ …+ а, содержащая k слагаемых)

Доказательство. Если a + а f а, то a + а + а f а + а, и т.д. В итоге получаем цепочку … f ka f… f 4а f3а f2а f а. В силу транзитивности и антисимметричности все элементы в ней различны. В группе цепочку можно продолжить в другую сторону, прибавляя элемент –а.

Следствие. Конечную полугруппу с сокращением, если чис­ло ее элементов не меньше 2, нельзя линейно упорядочить.

Теорема 7. Пусть áА, +, fñ – линейно упорядоченная группа. Тогда

Доказательство – в качестве упражнения.

Таким образом, всякая линейно упорядоченная группа либо строго, либо нестрого упорядочена. Для обозначения этих порядков будем пользоваться знаками > и ³ соответственно.

Упражнения

3.Докажите, что сумма положительных элементов линейно и строго упорядоченной полугруппы положительна.

4.Доказать, что всякий элемент линейно и строго упорядо­ченный полугруппы, больший положительного элемента, сам явля­ется положительным.

5.Докажите, что упорядоченная полугруппа линейно упоря­дочена в том и только в том случае, если любое конечное множество ее элементов имеет и только один наибольший элемент.

6.Докажите, что множество положительных элементов ли­нейно упорядоченной группы не пусто.

7.Пусть áА, +, fñ – линейно и строго упорядочен­ная группа. Докажите, что элемент а системы А тогда и только тогда положителен, если а > 0.

8.Докажите, что существует и только один линейный и стро­гий порядок в аддитивной полугруппе натуральных чисел, в кото­ром множество положительных элементов не пусто.

9.Докажите, что мультипликативную полугруппу целых чисел нельзя линейно упорядочить.

Упорядоченные кольца

Определение.Система áА, +, ×, fñ называется упорядоченным полукольцом, если

1) система áА, +, ×ñ – полукольцо;

2) система áА, +, fñ – упорядоченная полугруппа с непустым множеством А + положительных элементов;

3) выполняется монотонность относительно умножения на положительные элементы, то есть если сÎА + и а f b, то ac f bc, ca f cb.

Положительным элементом упорядоченного полукольца А называ­ется любой положительный элемент упорядоченной полугруппы áА, +, fñ.

Упорядоченное полукольцо áА, +, ×, fñ называ­ется упорядоченным кольцом (полем), если полукольцо áА, +, ×ñ – кольцо (соответственно поле).

Определение.Пусть áА, +, ×, fñ – упорядоченное полукольцо. Порядок f системы А называется архимедовым, а система А — архимедовски упорядоченной, если, каковы бы ни были по­ложительные элементы а и b системы А, можно указать такое на­туральное число п, что na f b.

Пример 1.Полукольцо натуральных чисел с отношением > (больше) – линейно, строго и архимедовски упорядоченное полукольцо.

Для линейно упорядоченного кольца áА, +, ×, 0, fñ система áА, +, 0, fñ – линейно упорядоченная группа. Отсюда следует согласно теореме 2.2.7, что порядок f либо строгий, либо нестрогий. Во мно­жестве А можно ввести (упражнения 2.1.5. и 2.1.6) новый линейный порядок, который будет строгим, если порядок f нестрогий, и нестрогим, если порядок f – строгий. В связи с этим замечанием в линейно упорядоченном кольце А обычно рассматривают два бинарных отношения порядка, одно из которых, строгое, обозначают знаком>, а второе, нестро­гое, знаком ³.

Для дальнейшего полезно напомнить, что в линейно упорядо­ченном кольце элемент а положителен тогда и только тогда, если а > 0 (упражнение 2.2.7).

Теорема 1. Пусть система áА, +, ×, 0, >ñ – линейно упоря­доченное кольцо. Тогда для любого элемента а из А либо а = 0, либо а > 0, либо –а > 0.

Доказательство. В силу линейности и строгости между элементами
а+ а и а имеет место одно и только одно из соотношений a+ a >a, a+ a = a, a+ a 0, то a –1 > 0.

Доказательство – в качестве упражнения.

Теорема 5. (Критерий порядка). Кольцо áА, +, ×, 0ñ тогда и только тогда можно линейно и строго упорядочить (т. е. ввести линейный и строгий порядок), если множество А имеет подмножест­во А + , удовлетворяющее условиям:

Доказательство. Пусть сначала áА, +, ×, 0, >ñ – линейно упорядоченное кольцо. В роли искомого подмножества А + в таком случае в силу теорем 1 и 2 может выступить множество положительных элементов системы А.

Пусть теперь А + – подмножество кольца áА, +, ×, 0ñ, удов­летворяю­щее условиям теоремы. Попробуем ввести линейный по­рядок > в кольце áА, +, ×, 0ñ. Определим это отношение так:

Легко проверяется, что введенное нами от­ношение связно, антирефлексивно, антисимметрично, транзитивно, монотонно относительно сложения и умножения на любой элемент из А + .

Множество А + с упомянутыми в условии теоремы 4 свойст­вами называют положительной частью кольца áА, +, ×, 0ñ. В даль­нейшем при введении порядка в каком-нибудь кольце мы будем искать в нем «положительную часть». Если такая часть в кольце существует, то кольцо можно упорядочить, если нет, то нельзя, если таких несовпадающих положительных частей несколько, то можно упорядочить несколькими способами.

Из сказанного следует, что при определении линейно упорядо­ченного кольца в качестве основного отношения вместо бинарного отношения > можно брать унарное отношение «положительная часть».

Теорема 6. (Критерий однозначности линейного порядка). Пусть А + и А ++ – положительные части кольца áА, +, ×, 0ñ. Тогда