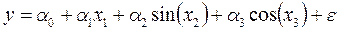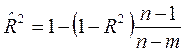Под полной мультиколлинеарностью понимается существование между некоторыми из факторов линейной функциональной связи. В практике статистических исследований полная мультиколлинеарность встречается достаточно редко, т.к. её несложно избежать уже на предварительной стадии анализа и отбора множества объясняющих переменных.
Реальная (или частичная) мультиколлинеарность возникает в случаях существования достаточно тесных линейных статистических связей между объясняющими переменными. Точных количественных критериев для определения наличия или отсутствия реальной мультиколлинеарности не существует.
Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной (явной) и стохастической (скрытой) формах.
При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица X`X особенная, так как содержит линейно зависимые векторы-столбцы, и её определитель равен нулю, т.е. нарушается предпосылка регрессионного анализа, это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели.
Однако в экономических исследованиях мультиколлинеарность чаще проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица X`X в этом случае является неособенной, но её определитель очень мал.
В то же время вектор оценок b и его ковариционная матрица ∑b пропорциональны обратной матрице (X`X) -1 , а значит, их элементы обратно пропорциональны величине определителя |X`X|. В результате получаются значительные средние квадратические отклонения (стандартные ошибки) коэффициентов регрессии b, b1,…,bp и оценка их значимости по t-критерию не имеет смысла, хотя в целом регрессионная модель может оказаться значимой по F-критерию.
Оценки становятся очень чувствительными к незначительному изменению результатов наблюдений и объёма выборки. Уравнения регрессии в этом случае, как правило, не имеют реального смысла, так как некоторые из его коэффициентов могут иметь неправильные с точки зрения экономической теории знаки и неоправданно большие значения.
Точных количественных критериев для определения наличия или отсутствия мультиколлинеарности не существует. Тем не менее, имеются некоторые эвристические подходы по её выявлению.
Один из таких подходов заключается в анализе корреляционной матрицы между объясняющими переменными X1,X2,…,Xp и выявлении пар переменных, имеющих высокие переменные корреляции (обычно больше 0,8). Если такие переменные существуют, говорят о мультиколлинеарности между ними. Полезно также находить множественные коэффициенты детерминации между одной из объясняющих переменных и некоторой группой из них. Наличие высокого множественного коэффициента детерминации (обычно больше 0,6) свидетельствует о мультиколлинеарности.
Другой подход состоит в исследовании матрицы X`X. Если определитель матрицы X`X либо её минимальное собственное значение λmin близки к нулю (например, одного порядка с накапливающимися ошибками вычислений), то это говорит о наличии мультиколлинеарности. О том же может свидетельствовать и значительное отклонение максимального собственного значения λmax матрицы X`X от её минимального собственного значения λmin.
Для устранения или уменьшения мультиколлинеарности используется ряд методов. Самый простой из них (но далеко не всегда возможный) состоит в том, что из двух объясняющих переменных, имеющих высокий коэффициент корреляции (больше 0,8), одну переменную исключают из рассмотрения. При этом, какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании экономических соображений. Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной.
Другой метод устранения или уменьшения мультиколлинеарности заключается в переходе от несмещённых оценок, определённых по методу наименьших квадратов, к смещённым оценкам, обладающим, однако, меньшим рассеянием относительно оцениваемого параметра, т.е. меньшим математическим ожиданием квадрата отклонения оценки bj от параметра βj или M (bj— βj) 2 .
Оценки, определяемые вектором, обладают в соответствии с теоремой Гаусса-Маркова минимальными дисперсиями в классе всех линейных несмещённых оценок, но при наличии мультиколлинеарности эти дисперсии могут оказаться слишком большими, и обращение к соответствующим смещённым оценкам может повысить точность оценивания параметров регрессии. На рисунке показан случай, когда смещённая оценка βj ^ , выборочное распределение которой задаётся плотностью φ( βj ^ ).
Действительно, пусть максимально допустимый по величине доверительный интервал для оцениваемого параметра βjесть (βj-Δ, βj+Δ). Тогда доверительная вероятность, или надёжность оценки, определяемая площадью под кривой распределения на интервале (βj-Δ, βj+Δ), как нетрудно видеть из рисунка, будет в данном случае больше для оценки βjпо сравнению с bj ( на рисунке эти площади заштрихованы). Соответственно средний квадрат отклонения оценки от оцениваемого параметра будет меньше для смещённой оценки, т.е.:
При использовании «ридж-регрессии» (или «гребневой регрессии») вместо несмещённых оценок рассматривают смещённые оценки, задаваемые вектором
гдеτ –некоторое положительное число, называемое «гребнем» или «хребтом»,
Ep+1 – единичная матрица (р+1) –го порядка.
Добавление τк диагональным элементам матрицы X`X делает оценки параметров модели смещёнными, но при этом увеличивается определитель матрицы системы нормальных уравнений – вместо (X`X) от будет равен
Таким образом, становится возможным исключение мультиколлинеарности в случае, когда определитель |X`X| близок к нулю.
Для устранения мультиколлинеарности может быть использован переходот исходных объясняющих переменныхX1,X2,…,Xn, связанных между собой достаточно тесной корреляционной зависимостью, к новым переменным, представляющим линейные комбинации исходных. При этом новые переменные должны быть слабокоррелированными либо вообще некоррелированными. В качестве таких переменных берут, например, так называемые главные компоненты вектора исходных объясняющих переменных, изучаемые в компонентном анализе, и рассматривают регрессию на главных компонентах, в которой последние выступают в качестве обобщённых объясняющих переменных, подлежащих в дальнейшем содержательной (экономической) интерпретации.
Ортогональность главных компонент предотвращает проявление эффекта мультиколлинеарности. Кроме того, применяемый метод позволяет ограничиться малым числом главных компонент при сравнительно большом количестве исходных объясняющих переменных.
Мультиколлинеарность — это понятие, которое используется для описания проблемы, когда нестрогая линейная зависимость между объясняющими переменными приводит к получению ненадежных оценок регрессии. Разумеется, такая зависимость совсем необязательно дает неудовлетворительные оценки. Если все другие условия благоприятствуют, т. е. если число наблюдений и выборочные дисперсии объясняющих переменных велики, а дисперсия случайного члена мала, то в итоге можно получить вполне хорошие оценки.
Итак, мультиколлинеарность должна вызываться сочетанием нестрогой зависимости и одного (или более) неблагоприятного условия, и это — вопрос степени выраженности явления, а не его вида. Оценка любой регрессии будет страдать от нее в определенной степени, если только все независимые переменные не окажутся абсолютно некоррелированными. Рассмотрение данной проблемы начинается только тогда, когда это серьезно влияет на результаты оценки регрессии.
Эта проблема является обычной для регрессий временных рядов, т. е. когда данные состоят из ряда наблюдений в течение какого-то периода времени. Если две или более независимые переменные имеют ярко выраженный временной тренд, то они будут тесно коррелированы, и это может привести к мультиколлинеарности.
Перечислим основные последствия мультиколлинеарности:
1. Большие дисперсии оценок. Это затрудняет нахождение истинных значений определяемых величин и расширяет интервальные оценки, ухудшая их точность.
2. Уменьшаются t – статистики коэффициентов, что может привести к неоправданному выводу о несущественности влияния соответствующего фактора на зависимую переменную.
3. Оценки коэффициентов по МНК и их стандартные ошибки становятся очень чувствительными к малейшим изменениям данных, т.е. они становятся неустойчивыми.
4. Затрудняется определение вклада каждой из объясняющих переменных в объясняемую уравнением регрессии дисперсию зависимой переменной.
5. Возможно получение неверного знака у коэффициента регрессии.
Единого подхода к устранению мультиколлинеарности не существует. Существует ряд методов, которые не являются универсальными и применимы в конкретных ситуациях.
Простейшим методом устранения мультиколлинеарности является исключение из модели одной или нескольких коррелированных переменных. Здесь необходима осторожность, чтобы не отбросить переменную, которая необходима в модели по своей экономической сущности, но зачастую коррелирует с другими переменными (например, цена блага и цены заменителей данного блага).
Иногда для устранения мультиколлинеарности достаточно увеличить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным. Это приведёт к сокращению дисперсии коэффициентов регрессии и увеличению их статистической значимости. Однако при этом можно усилить автокорреляцию, что ограничивает возможности такого подхода.
В некоторых случаях изменение спецификации модели, например, добавление существенного фактора, решает проблему мультиколлинеарности. При этом уменьшается остаточная СКО, что приводит к уменьшению стандартных ошибок коэффициентов.
В ряде случаев минимизировать либо вообще устранить проблему мультиколлинеарности можно с помощью преобразования переменных.
Теперь рассмотрим другой вопрос, имеющий важное значение для проблем, связанных со спецификацией модели множественной регрессии. Это частная корреляция. С помощью частных коэффициентов корреляции проводится ранжирование факторов по степени их влияния на результат. Кроме того, частные показатели корреляции широко используются при решении проблем отбора факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в модель нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Высокое значение коэффициента парной корреляции между исследуемой зависимой и какой – либо независимой переменной может означать высокую степень взаимосвязи, но может быть обусловлено и другой причиной, например, третьей переменной, которая оказывает сильное влияние на две первые, что и объясняет их высокую коррелированность. Поэтому возникает задача найти «чистую» корреляцию между двумя переменными, исключив (линейное) влияние других факторов. Это можно сделать с помощью коэффициента частной корреляции.
Коэффициенты частной корреляции определяются различными способами.
Теперь остановимся на специальных процедурах спецификации модели множественной регрессии, которые обычно называются процедурами пошагового отбора переменных.
Иногда исследователь заранее знает характер зависимости исследуемых величин, опираясь на экономическую теорию, предыдущие результаты или априорные знания, и его задача состоит лишь в оценивании неизвестных параметров. Классическим примером является оценивание параметров производственной функции Кобба – Дугласа, где заранее известно, что в качестве факторов выступают капиталовложения и трудозатраты.
Однако на практике чаще имеется большое число наблюдений различных независимых переменных, но нет априорной модели изучаемого явления. Возникает проблема, какие переменные включать в регрессионную схему.
В компьютерные пакеты включены различные эвристрические процедуры пошагового отбора факторов. Основными пошаговыми процедурами являются:
— процедура последовательного присоединения;
— процедура последовательного присоединения – удаления;
— процедура последовательного удаления.
Следует признать, что пошаговые процедуры, не гарантируют получения оптимального (в смысле критерия максимума коэффициента детерминации) набора факторов. Однако в подавляющем большинстве ситуаций получаемые с помощью пошаговой процедуры наборы переменных оказываются оптимальными или близкими к оптимальным.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9116 — 

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
6. Теорема Гаусса-Маркова для парной регрессии и определение дисперсии коэффициентов регрессии.
7. Характеристики качества для парной регрессии. Геометрическая интерпретация. Статистическая проверка их значимости.
8. Интервал прогнозирования. Доверительные интервалы для коэффициентов регрессии.
9. МНК для парной регрессии на случай стохастического регрессора. Статистические свойства полученных оценок.
10. Оценка максимального правдоподобия параметров парной регрессии.
11. МНК для множественной регрессии. Доказательство статистических свойств оценок для моментов регрессии.
12. Теорема Гаусса-Маркова для множественной регрессии. Определение ковариационно-дисперсионной матрицы вектора коэффициентов регрессии.
13. Характеристики тесноты статистической связи в множественном регрессионном анализе.
14. Критериальная проверка качества множественной регрессии.
15. Коэффициенты эластичности для парной и множественной регрессии.
16. Проблема мультиколлинеарности. Примеры. Геометрическая интерпретация. Практические пути ее решения.
17. Обобщение МНК множественной регрессии на случай стохастических регрессоров.
18. Проблема гетероскедастичности. Примеры. Геометрическая интерпретация. Практические пути ее решения.
19. Обобщение МНК на случай непостоянства ковариационно-дисперсионной матрицы ошибки. Статистические методы тестирования дисперсии ошибки.
20. Доступные методы реализации МНК при непостоянстве дисперсии ошибки.
21. Проблема учета качественных переменных в регрессионном анализе. Практические примеры. Построение регрессионной модели. Критериальная проверка.
22. Линейная эконометрическая модель. Переменные модели. Обоснование формы эконометрического уравнения и линеаризация модели. Отбор факторов.
23. Процедура построения эконометрической модели. Характеристики и критерии качества эконометрической модели. Значимость влияния факторов и критерии ее проверки. Взаимосвязи между критериями значимости факторов и критериями качества модели.
24. МНК, критерий метода, процедура МНК.
25. ММП, критерий метода, процедура ММП.
26. Фактическая и теоретическая ошибки модели. Желательные свойства теоретической ошибки. Критерии проверки свойств фактической ошибки.
27. Ковариационные матрицы ошибок и оценок параметров эконометрических моделей, взаимосвязи между этими матрицами.
28. Оценивание параметров линейной эконометрической модели с учетом ограничений.
29. Обобщенный МНК и условия его применения. Особенности использования ОМНК в модели с коррелированными и гетероскедастичными ошибками. Двухшаговый МНК.
30. Рекуррентные методы оценки параметров эконометрических моделей. Рекуррентная процедура обращения матрицы (Х’Х).
31. Метод главных компонент. Его преимущества и недостатки при построении моделей. Компоненты и факторы, их взаимосвязи.
32. Модели с лаговыми независимыми переменными. Основные подходы и процедуры оценки их параметров. Метод Ш. Алмон.
33. Модели с лаговыми зависимыми переменными. Проблемы оценки их параметров. Схема Койка.
34. Двухшаговый МНК и особенности его применения в моделях с лаговыми зависимыми переменными. Инструментальные переменные, их содержание и особенности формирования.
35. Системы взаимозависимых эконометрических моделей. Свойства моделей и их влияние на качество оценок параметров. Структурная и приведенная формы системы моделей. Основные подходы к оценке параметров уравнений. Двухшаговый МНК.
36. Процедуры и методы оценки параметров нелинейных эконометрических моделей. Критерии методов. Метод прямого поиска. Проблемы его реализации на практике. Методы, использующие линеаризацию уравнения модели и линеаризацию целевой функции. Градиентные методы.
Примеры тестов для контроля знаний
1. Показатель, характеризующий тесноту линейной стохастической связи между переменными — это…
б) коэффициент корреляции
г) все варианты а)-в) верны
д) среди вариантов а)-г) нет верного
2. Функция регрессии в общем случае является…
а) математическим выражением функциональной зависимости между переменными
б) математическим выражением корреляционной связи между переменными
в) математическим выражением исключительно линейной связи между переменными
г) математическим выражением любого рода зависимости между переменными
д) среди вариантов а)-г) нет верного
а) переменные y и x связаны между собой линейно
б) связь между y и x является стохастической
в) на переменную y не оказывают влияния никакие факторы, кроме x
г) с ростом переменной x на одну единицу y увеличивается на β единиц
д) среди вариантов а)-г) нет верного
а) означает постоянство дисперсии случайного члена регрессионного уравнения
б) предполагает отсутствие корреляционной связи между случайным членом и объясняющими переменными регрессионной модели
в) является одним из условий классической модели линейной регрессии
г) верны варианты а) и в)
д) верны варианты б) и в)
5. Одним из условий классической линейной регрессионной модели является…
а) отсутствие какого-либо влияния на y со стороны факторов, не включенных в модель явно
б) отсутствие среди объясняющих факторов дискретных переменных
в) отсутствие автокорреляции случайного члена
г) верны варианты а) и б)
д) среди вариантов а)-г) нет верного
6. Каким свойством обладают оценки коэффициентов классической модели, полученные с помощью метода наименьших квадратов?
г) все ответы а)-в) верны
д) среди вариантов а)-г) нет верного
7. Как формулируется нулевая гипотеза при проверке коэффициента уравнения регрессии на статистическую значимость?
а) оценка коэффициента равна нулю
б) оценка коэффициента положительна
в) оценка коэффициента отрицательна
г) дисперсия оценки коэффициента минимальна
д) среди вариантов а)-г) нет верного
8. Какая формулировка нулевой гипотезы не используется при проверке уравнения регрессии на статистическую значимость?
а) коэффициент детерминации в полученном уравнении равен нулю
б) все коэффициенты при объясняющих переменных равны нулю
в) свободный член полученного уравнения равен нулю
г) все варианты а)-в) верны
г) среди вариантов а)-г) нет верного
9. Какой факт не может свидетельствовать о наличии мультиколлинеарности?
а) коэффициенты парной корреляции результирующего признака с каждым из объясняющих факторов по модулю близки к единице
б) некоторые коэффициенты парной корреляции среди объясняющих факторов по модулю близки к единице
в) коэффициенты множественной детерминации некоторых объясняющих факторов с остальными близки к единице
г) неверный, с точки зрения экономической теории, знак коэффициента линейного регрессионного уравнения
д) среди вариантов а)-г) нет верного
10. В каком случае целесообразно использовать метод главных компонент?
а) если метод наименьших квадратов дает статистически незначимое уравнение
б) если объясняющие факторы коррелируют между собой
в) если свободный член полученного уравнения равен нулю
г) есди колическтво наблюдений недостаточно велико по сравнению с числом объясняющих факторов
д) среди вариантов а)-г) нет верного
11. Взвешенный метод наименьших квадратов…
а) применяется в случае гетероскедастичных остатков
б) предполагает упорядочение исходных наблюдений по возрастанию/убыванию
в) предполагает придание «веса» каждому наблюдению в определенном соответствии с величиной его дисперсии
г) верны варианты а) и в)
д) среди вариантов а)-г) нет верного
12. Каковы негативные последствия применения классического метода наименьших квадратов в случае гетероскедастичности?
а) оценки коэффициентов модели не являются состоятельными
б) оценки коэффициентов модели не являются статистически значимыми
в) оценки коэффициентов модели не являются эффективными
г) оценки коэффициентов модели являются смещенными
д) все варианты а)-г) верны
13. В каких задачах следует ожидать наличия гетероскедастичности?
а) когда анализируются определенные статьи расходов хозяйствующих субъектов в зависимости от величины их доходов и последние имеют значительный разброс
б) когда в выборке присутствуют наблюдения, сильно отличающиеся от большинства остальных
в) когда анализируются временные ряды и наблюденные значения существенно изменяются со временем или данные пространственных выборок определенным образом упорядочены
г) все варианты а)–в) верны
д) среди вариантов а)-г) нет верного
14. Об автокорреляции остатков можно сказать, что…
а) факт ее существования устанавливается с помощью критерия Дарбина-Уотсона
б) она часто встречается в задачах, где исходными данными являются временные ряды
в) ее следствием, в частности, является неэффективность оценок параметров регрессионного уравнения
г) в случае ее существования следует применять обобщенный метод наименьших квадратов
д) все варианты а)-г) верны
15. Для отражения влияния на структуру модели качественных переменных, если они наблюдаемы, применяют…
а) фальшивые переменные
б) фиктивные переменные
в) поддельные переменные
г) искусственные переменные
д) среди вариантов а)-г) нет верного
16. Какая из приведенных ниже моделей не поддается непосредственной линеаризации?
д) среди вариантов а)-в) нет верного
17. Что из перечисленного ниже не применяют для оценки параметров нелинеаризуемых моделей?
а) итеративные процедуры
б) метод наименьших квадратов
в) метод максимального правдоподобия
г) верны варианты б) и в)
д) среди вариантов а)-г) нет верного
18. При использовании метода максимального правдоподобия…
а) отыскиваются параметры модели, наиболее вероятные для данного набора наблюдений
б) отыскивается набор наблюдений, оптимизирующий параметры модели
в) оценивается вероятность, с которой набор параметров модели принимает оптимальные значения
г) верны варианты а) и в)
д) среди вариантов а)-г) нет верного
19. Среди переменных в системах одновременных линейных уравнений специально выделяют…
а) результирующие и объясняющие
б) случайные и детерминированные
в) эндогенные и экзогенные
г) фиктивные и обычные
г) все варианты а)-в) верны
20. Почему для оценки параметров системы линейных одновременных уравнений нельзя применять одношаговый МНК?
а) из-за смещения получаемых оценок
б) из-за несостоятельности получаемых оценок
в) из-за некорректности проводимых статистических тестов
г) все варианты а)-в) верны
д) среди вариантов а)-г) нет верного
21. Какие методы не применяются для оценки параметров системы линейных одновременных уравнений?
а) косвенный метод наименьших квадратов
б) двухшаговый метод наименьших квадратов
в) трехшаговый метод наименьших квадратов
г) не применяется ни один из методов а)-в)
д) среди вариантов а)-г) нет верного
VI. ТЕМАТИЧЕСКИЙ План ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
Самостоя-тельная работа (формы, часы)
Интерак-тивные формы обучения
Формы текущего контроля
Проблемы обоснования эконометрической модели
Промежуточный отчет по проекту
Методы оценки параметров линейных эконометрических моделей
Промежуточный отчет по проекту
Методы оценки коэффициентов эконометрической модели при коррелирующих или нестандартных ошибках
Промежуточный отчет по проекту
Модели с коррелирующими факторами
Отчет по деловой игре «Выбор подхода к оценке параметров модели с коррелирующими факторами».
Модели с лаговыми зависимыми переменными
Линейные регрессионные модели с атрибутивными факторами
.
Проверим правильность обращения матрицы А. Должно выполняться равенство: АА-1 = Е, где Е — единичная матрица:
.
В результате проверки получена единичная матрица, что и требовалось показать.
Обратим внимание на то, что матрица А достаточно близка к особенной. Действительно, если бы элемент а22 равнялся не 2,9, а 3,0, то определитель çА ç = 0, деление на 0 невозможно, А-1 не существует. Обратим также внимание на то, что при а22 =3,0 столбцы линейно зависимы: второй столбец получается из первого делением на 2: А2=А1/2. Это случай функциональной зависимости. Нарушается предпосылка-6 множественной регрессии.
На практике чаще бывают случаи, когда взаимосвязь между переменными Х1, Х2, … , Хp носит статистический характер. При высокой взаимной коррелированности объясняющих переменных определитель квадратной матрицы X’X может очень близко приближаться к нулю. А поскольку вектор оценок b и его ковариационная матрица åb пропорциональны (X’X)-1X’Y, получаются большие средние квадратические отклонения коэффициентов b и оценка их по t-критерию Стьюдента не имеет смысла, хотя в целом по F-критерию модель может быть значимой.
При высокой мультиколлинеарности оценки становятся очень чувствительными к малым изменениям наблюденных данных, включая объем выборки. Уравнение регрессии содержательно не интерпретируется, так как некоторые его коэффициенты могут иметь неверные с точки зрения экономической теории (смысла) знаки и неоправданно большие значения.
Существуют различные подходы, в том числе и эвристические, к выявлению и снижению степени мультиколлинеарности.
Первый подход основан на анализе корреляционной матрицы между объясняющими переменными. Признак мультиколлинеарности здесь — наличие парных коэффициентов корреляции со значениями от ç0,7ç и выше. Трудно проследить цепочку взаимозависимости между переменными. Обычно это удается для числа переменных не более 4-х. Некоторые из тесно связанных между собой объясняющих переменных исключаются из списка претендентов, а вместо них могут включаться другие. И так несколько раз.
Второй подход — находить коэффициенты детерминации одной из объясняющих переменных в зависимости от групп других объясняющих переменных. Признак мультиколлинеарности здесь — наличие коэффициента детерминации со значением больше 0,6. Для снижения мультиколлинеарности такие группы переменных исключаются. Вместо них в соответствии с гипотезой о данном явлении вводятся другие переменные. Процедура может повторяться.
Третий подход — исследование матрицы X’X. Если ее определитель близок по модулю к нулю (это еще зависит и от единиц измерения), например, çX’Xç = 0,000013, то это может свидетельствовать о наличии мультиколлинеарности. Далее можно применить эффективную процедуру отбора значащих факторов, которую назовем методом вращения факторов. В качестве основного критерия уместно использовать остаточную дисперсию — несмещенную выборочную оценку s2 параметра s2 возмущений e:
/.
Опишем процедуру отбора факторов методом вращения подробно. Пусть из теоретических соображений для объяснений изменения Y мы отобрали 6 объясняющих факторов-претендентов. Проверка показала высокую мультиколлинеарность. В произвольном порядке присваиваем переменным имена (для удобства буквенные): Xa, Xb, Xc, Xd, Xe, Xf. Затем строим шесть уравнений регрессий с факторами: (Xa), (Xa, Xb), (Xa, Xb, Xc), (Xa, Xb, Xc, Xd), (Xa, Xb, Xc, Xd, Xe), (Xa, Xb, Xc, Xd, Xe, Xf). Для каждого уравнения вычисляем остаточную дисперсию s2 и откладываем эти значения на графике рис. 4.1, верхняя ломаная. Как видно, каждая новая переменная, включенная в регрессию по порядку, примерно на одинаковую величину уменьшает остаточную дисперсию. Вывод: все факторы примерно одинаково значимы, и в уравнение нужно включить их все.
Тема 4. Множественный регрессионный анализ
4.1 Спецификация модели множественной регрессии
4.2 Вычисление параметров линейной множественной регрессионной модели при помощи МНК.
4.3 Оценка влияния различных факторов на зависимую переменную
4.4 Оценка качества множественных регрессионных моделей
4.5 Мультиколлинеарность и методы ее устранения
4.6 Проблемы построения качественной регрессионной модели
Основные положения
Множественная регрессионная модель (множественная регрессия) представляет собой модель, связывающую несколько независимых (объясняющих) переменных с одной результативной. Общий вид модели, включающей m независимых переменных:

Обычно рассматривают линейную модель, поскольку, как было показано в предыдущей теме, большинство нелинейных моделей достаточно легко сводятся к линейной путем линеаризации. Спецификация модели линейной множественной регрессии имеет вид:

Уравнение линейной множественной регрессии будет выглядеть следующим образом:

В случае применения множественного регрессионного анализа особое внимание следует уделить вопросам отбора переменных для анализа. Для этого используются два подхода: «сверху вниз» и «снизу вверх». Достоинства и недостатки каждого подхода были рассмотрены в теме 1, поэтому мы сразу затронем вопрос практической их реализации. На первом этапе построения модели составляется матрица корреляции размером (m+1) x (m+1), где m – общее число всех возможных независимых переменных (факторов). В нее помещаются коэффициенты корреляции между факторами и результативным признаком, а также попарно между всеми факторами. В ячейке rij указывается коэффициент корреляции между i-м и j-м фактором. Эта матрица будет симметричной относительно главной диагонали, причем на диагонали будут значения, равные 1:
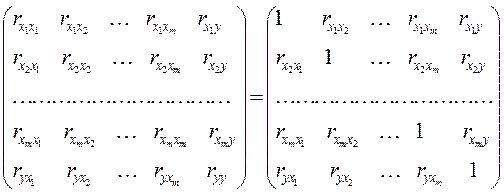
После этого в модель включаются факторы, для которых значение rij по модулю больше заданного критического значения. Обычно критическое значение устанавливают на уровнях 0.5 – 0.9. В то же время не следует включать в модель переменные, между которыми наблюдается тесная взаимосвязь (высокие значения rijв соответствующей ячейке). невыполнение этого условия может привести к некорректному построению модели (см. мультиколлинеарность).
По аналогии с парной регрессией для определения параметров множественной регрессии могут использоваться различные методы, однако чаще всего применяется МНК. Для его применения необходимо выполнение следующих предпосылок:
1. Математическое ожидание случайного отклонения равно 0 для всех наблюдений M(ε)=0
2. Дисперсия случайных отклонений постоянна
3. Случайные отклонения независимы друг от друга
4. Случайное отклонение независимо от объясняющих переменных регрессионной модели:
5. Модель линейна относительно параметров
6. Отсутствие сильной взаимозависимости между объясняющими переменными
7. Случайные ошибки имеют нормальное распределение
При выполнении перечисленных предпосылок неизвестные коэффициенты уравнения регрессии a1, a2, … am найдутся из решения системы уравнений:

где количество уравнений совпадает с числом переменных (m+1), а суммирование осуществляется по выборке из n единиц.
Эта система может быть решена либо каким-нибудь из вычислительных методов линейной алгебры (например, методом Жордана-Гаусса), либо при помощи компьютера (в частности, такая функция реализуется в MS Excel).
Для множественной регрессионной модели актуален вопрос о том, какова сила влияния различных факторов на значение зависимой переменной. Для этого используются два основных метода. Первый основан на построении регрессионной модели в стандартизированной форме, второй – на расчете частных коэффициентов эластичности.
Для преобразования модели к стандартизованной форме осуществляют переход к новым переменным:

уравнение множественной регрессии примет вид:

Оценив параметры этой модели по МНК, по значениям параметров βj при каждой переменной мы можем сделать вывод о сравнительной силе влияния различенных факторов. Большее значение коэффициента говорит о большей силе влияния соответствующего фактора на зависимую переменную, положительное значение – о прямом влиянии, отрицательное – об обратном.
Частные коэффициенты эластичности рассчитываются по формулам:

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении зависимой на 1 процент и неизменности действия прочих факторов.
Оценка качества построенной модели проводится по тем же этапам, что и для парной регрессии (см. рис. 3.4):
1. Анализ адекватности модели в целом
2. Анализ точности определения оценок коэффициентов регрессии (расчет их дисперсии и стандартного отклонения)
3. Проверка статистической значимости коэффициентов регрессии
4. Интервальная оценка коэффициентов регрессионного уравнения
5. Определение доверительных интервалов для зависимой переменной
Логика всех этапов аналогична парной регрессии.
1. Оценка адекватности модели в целом осуществляется на основе расчета коэффициента детерминации 


После несложных преобразований получаем выражение для 


из последней формулы видно, что скорректированный коэффициент детерминации меньше обычного коэффициента детерминации и, следовательно, является более строгим показателем связи, чем 
Отметим, что корректировка может производиться, только если выполняется соотношение:

После определения значения коэффициента детерминации следует проанализировать его статистическую значимость. Статистическая значимость проверяется путем проверки гипотезы о равенстве коэффициента детерминации 0. Если гипотеза отвергается, то делается вывод о том, что коэффициент детерминации отличен от 0 и статистически значим. Для проверки используют F-статистику:

Полученное фактическое значение сравнивают с критическим Fα;m;n—m-1, если оно оказывается больше критического, то нулевая гипотеза отвергается и делается вывод о статистической значимости коэффициента детерминации и существенности построенной модели. В противном случае модель нельзя использовать на практике.
Для множественной регрессии оценка качества модели в целом также может осуществляться с использованием средней ошибки аппроксимации:

Если значение 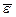
2. Расчет дисперсии коэффициентов регрессионного уравнения. Точный расчет производится с использованием элементов матричной алгебры и отводится на самостоятельное изучение. Приближенное же вычисление дисперсии можно осуществить по формуле:

где Ri–коэффициент полной корреляции i-й переменной с остальными независимыми переменными (может быть определен как корень квадратный коэффициента детерминации регрессионной модели 

Рассмотрим одну из существенных проблем, возникающих при применении множественного регрессионного анализа – мультиколлинеарности. Под мультиколлинеарностью понимают тесную линейную взаимосвязь объясняющих переменных (рис. 4.1 и 4.2). Термин мультиколлинеарность введен Р. Фришем.
Рис. 4.1 Мультиколлинеарность между x1 и x2
a) мультиколлиенеарности нет; b) умеренная мультиколлиенарность;
с) сильная мультиколлинеарность;
d) совершенная мультиколлинеарность
В случаях, проиллюстрированных на рис. 4.1 a) и b) в модель можно включать обе независимые переменные, а в случаях с) и d) –только одну из двух переменных.
Проблема мультиколлинеарности связана, прежде всего, со следующими ее последствиями (рис. 4.2).
1. Высокие значения дисперсии оценок коэффициентов, что приводит к ухудшению точности их интервальных оценок, а также уменьшению t-статистик коэффициентов, что может привести к неправильному выводу о несущественности влияния независимой переменной на зависимую.
2. Оценки коэффициентов, полученные по МНК, становятся очень чувствительными к изменениям исходных данных.
Рис. 4.2 Причины, последствия, методы обнаружения и устранения мультиколлинеарности
3. Затрудняется измерение вклада каждой из объясняющих переменных в объясняемую уравнением регрессии дисперсию зависимой переменной.
4. Возможно получение неверного знака у коэффициента перед объясняющей переменной.
В то же время при достаточно высоких значениях коэффициента детерминации в моделях, построенных для цели прогнозирования, мультиколлинеарность не является достаточно серьезной проблемой, и построенные модели вполне могут быть использованы на практике.
Проблема мультиколлинеарности обязательно должна быть решена в том случае, если целью модели является анализ характера влияния различных факторов на зависимую переменную.
Мультиколлиеарность можно определить при помощи следующих методов:
1. Анализ значений коэффициентов корреляции между объясняющими переменными. Высокие коэффициенты корреляции между объясняющими переменными
2. Сопоставление коэффициента детерминации и статистической значимости коэффициентов в модели. Коэффициент детерминации модели достаточно высок, но некоторые из коэффициентов в модели статистически незначимы.
3. Анализ вспомогательной регрессии – регрессии между объясняющими переменными. Для обнаружения регрессионной зависимости между объясняющими переменными строятся регрессионные модели типа:

где j не равно i
для каждой объясняющей переменной.
Затем при помощи критерия Фишера (F-статистики) проверяется ее статистическая значимость:
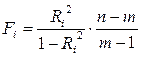
Полученное значение сравнивается с критическим Fα;m-1;n—m. Если значение Fi оказывается больше критического, то делается вывод о том, что i-я независимая переменная является линейной комбинацией других и, следовательно, в модели присутствует мультиколлинеарность.
4. Анализ определителя матрицы корреляции независимых переменных.
Этот метод основан на том, что матрица, составленная из коэффициентов корреляции между объясняющими переменными, в случае отсутствия мультиколлинеарности имела бы определитель, равный единице (4. 11):
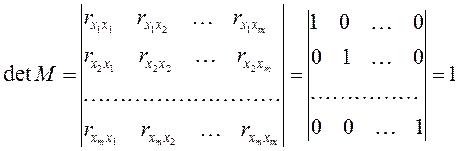
При существовании мультиколлинеарности коэффициенты отличны от 0 (изменяются в пределах от –1 до 1), и определитель матрицы становится меньше. В случае совершенной мультиколлинеарности он равен 0:

Обнаружить мультиколлинеарность можно, проверив статистическую гипотезу по поводу равенства 1 определителя этой матрицы:
Проверка осуществляется на основе критерия χ 2 (хи –квадрат). Доказано, что величина:

имеет распределение χ 2 с 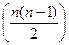
Рассмотрим методы устранения мультиколлинеакрности.
1. Исключение коррелированных переменных из модели. Это наиболее простой способ борьбы с мультиколлинеарностью. Однако в этом случае возможны серьезные проблемы, связанные с тем, что полученные по упрощенной модели оценки будут смещенными.
2. Получение дополнительных данных или проведение нового наблюдения. Часто мультиколлинеарность проявляется вследствие неполноты данных, и при расширении выборки существенно уменьшается. Однако этот подход связан со значительными издержками, и, кроме того, может быть связан с появлением такого нежелательного явления, как автокорреляция.
3. Изменение спецификации модели. Может быть осуществлено как при помощи изменения аналитического выражения модели, так и путем добавления новых переменных, оказывающих существенное влияние на зависимую переменную. Этот метод целесообразно применять, если добавляемая переменная является «полезной», то есть существенно улучшает качество модели.
4. Использование предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров модели могут быть определены по пробным выборочным наблюдениям, тогда мультиколлинеарность может быть устранена путем установления значений параметра у одной коррелирующих переменных. Ограниченность метода – в сложности получения предварительных значений параметров с высокой точностью.
5. Преобразование переменных. Для устранения мультиколлинеарности можно преобразовать переменные, например, путем линеаризации или получения относительных показателей, а также перехода от номинальных к реальным показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки зрения обеспечения ее высокого качества возникают следующие вопросы:
1. Каковы признаки качественной модели?
2. Какие ошибки спецификации могут быть?
3. Каковы последствия ошибок спецификации?
4. Какие существуют методы обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели множественной регрессии:
1. Простота. Из двух моделей примерно одинаковых статистических свойств более качественной является та, которая содержит меньше переменных, или же более простая по аналитической форме.
2. Однозначность. Метод вычисления коэффициентов должен быть одинаков для любых наборов данных.
3. Максимальное соответствие. Этот признак говорит о том, что основным критерием качества модели является коэффициент детерминации, отражающий объясненную моделью вариацию зависимой переменной. Для практического использования выбирают модель, для которой расчетное значение F-критерия для коэффициента детерминации б четыре раза больше табличного.
4. Согласованность с теорией. Получаемые значения коэффициентов должны быть интерпретируемы с точки зрения экономических явлений и процессов. К примеру, если строится линейная регрессионная модель спроса на товар, то соответствующий коэффициент при цене товара должен быть отрицательным.
5. Хорошие прогнозные качества. Обязательным условием построения качественной модели является возможность ее использования для прогнозирования.
Одной из основных ошибок, допускаемых при построении регрессионной модели, является ошибка спецификации (рис. 4.3). Под ошибкой спецификации понимается неправильный выбор функциональной формы модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1. Невключение в модель полезной (значимой) переменной.
2. Добавление в модель лишней (незначимой) переменной
3. Выбор неправильной функциональной формы модели
Последствия ошибки первого вида (невключение в модель значимой переменной) заключаются в том, что полученные по МНК оценки параметров являются смещенными и несостоятельными, а значение коэффициента детерминации значительно снижаются.
При добавлении в модель лишней переменной (ошибка второго вида) ухудшаются статистические свойства оценок коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели и затрудняет содержательную интерпретацию параметров, однако по сравнению с другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор функциональной формы модели, то есть допущена ошибка третьего вида, то получаемые оценки будут смещенными, качество модели в целом и отдельных коэффициентов будет невысоким. Это может существенно сказаться на прогнозных качествах модели.
Ошибки спецификации первого вида можно обнаружить только по невысокому качеству модели, низким значениям R 2 .
Обнаружение ошибок спецификации второго вида, если лишней является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной регрессионной модели
Если же таких переменных несколько, целесообразно прибегнуть к сравнению значений коэффициентов детерминации модели до и после исключения из модели переменных, которые считаются лишними, при помощи расчета F-критерия по формуле:

где m1 – число объясняющих переменных в первоначальном уравнении, m2 – число объясняющих переменных в уравнении после отброса лишних переменных.
Полученное значение сравнивается с критическим F α;m1–m2;n–m1–1. Если расчетное значение меньше, то считается, что исключенные из модели переменные являются лишними.
Ошибки третьего вида можно обнаружить только при помощи содержательной интерпретации модели или визуально анализируя данные или по наличию гетероскедастичности (см. тему 7).
Комплексный анализ ошибок спецификации можно провести, выполнив один или несколько из следующих тестов:
1) Тест Рамсея (Regression specification error test – RESET);
2) Тест максимального правдоподобия (The Likelihood Ratio test);
3) Тест Валда (The Wald test);
4) Тест множителя Лагранжа (The Lagrange multiplier test);
5) Тест Хаусманна (The Hausmann test)
6) Преобразование Бокса-Кокса (Box-Cox transformation)
Вопросы для самоконтроля
1. Дайте определение множественной регрессионной модели.
2. Каким образом осуществляется выбор переменных, включаемых в модель?
3. Выполнение каких предпосылок необходимо для применения МНК?
4. Какое количество уравнений в системе, решение которой дает оценку параметров МНК?
5. Какие особенности оценки качества модели множественной регрессии Вы можете назвать?
6. Каким образом оценивается статистическая значимость коэффициента детерминации?
7. Что такое мультиколлинеарность?
8. Какие последствия мультиколлинеарности Вы знаете?
9. Перечислите методы определения мультиколлинеарности.
10. Опишите методы устранения мультиколлинеарности.
11. Назовите основные признаки качественной модели.
12. Что такое ошибка спецификации?
13. Какие виды ошибок спецификации Вы знаете? В чем их суть?
14. Каким образом можно обнаружить ошибки спецификации?
15. Перечислите способы ошибок спецификации
Задания и задачи
1. Запишите спецификацию модели множественной линейной регрессии:
a) рыночного спроса
b) рыночного предложения
c) совокупных расходов в кейнсианской модели «доходы — расходы»
d) рациональных ожиданий
e) трансакционных издержек
2. Проведите линеаризацию следующих моделей множественной регрессии:
a)
b)
c)
3. По данным таблицы построить матрицу корреляции и разработать модель множественной регрессии, которая анализирует факторы, влияющие на объемы продаж в магазинах:
| № | Qd (объем спроса) | P (цена товара, руб.) | L (расстояние от центра города, в км) | Pз. (цена товара-заменителя, руб.) | t (время существования магазина, лет) |
| 2.5 | |||||
| 2.3 | |||||
| 2.4 | |||||
| 2.2 | |||||
| 2.4 | |||||
| 2.1 | |||||
| 2.0 | |||||
| 2.0 | |||||
| 1.8 | |||||
| 1.9 | |||||
| 2.1 | |||||
| 1.8 |
4. Оцените качество полученной в предыдущем задании модели.
5. Оцените статистическую значимость коэффициентов линейной регрессионной модели Qd = f(P,L, Pв3/3,t) из задания 3.
6. Определите наличие (отсутствие) мультиколлинеарности в модели из задания 3 различными методами.
7. Оцените параметры ПФ Кобба-Дугласа по следующим данным:
| № п/п | Q | L | K |
| 1. | |||
| 2. | |||
| 3. | |||
| 4. | |||
| 5. | |||
| 6. | |||
| 7. | |||
| 8. | |||
| 9. | |||
| 10. |
8. Оцените параметры линейной производственной функции, производственной функции Кобба-Дугласа и производственной функции Леонтьева по следующим эмпирическим данным. Какая функция точнее описывает фактическую зависимость?
Объемы производства (Q), млн. руб.
| Объем используемого труда (L), человек | ||||||
| Объем используемого капитала (K), млн. руб. | ||||||
| 78,8 | 79,5 | 79,2 | 81,5 | 82,7 | 81,7 | 84,3 |
| 91,1 | 92,1 | 92,0 | 92,7 | 93,8 | 97,4 | 98,0 |
| 101,7 | 104,1 | 104,8 | 104,7 | 106,1 | 110,3 | 108,4 |
| 112,8 | 115,3 | 115,2 | 116,8 | 120,1 | 121,6 | 120,4 |
| 122,9 | 125,7 | 128,1 | 129,7 | 131,4 | 133,5 | 135,8 |
| 134,5 | 135,7 | 139,0 | 141,9 | 142,1 | 142,1 | 146,5 |
| 144,3 | 147,6 | 147,3 | 153,0 | 154,7 | 155,5 | 156,3 |
9. Если в результате построенной вспомогательной регрессии в модели (m=5, n=100) получились следующие результаты:
Какие переменные следует исключить из модели и почему?
Тесты
1. Если m – количество объясняющих переменных, а n – количество единиц наблюдения, то в каком из перечисленных случаев регрессионная модель будет, при прочих равных условиях, наилучшего качества?
2. Скорректированный коэффициент детерминации 
d) Равен R 2 при n > 25
3. Входит ли отсутствие мультиколлинеарности в число предпосылок применения МНК для расчета параметров модели множественной регрессии?
4. Возможен ли расчет доверительного интервала для зависимой переменной в случае множественной регрессионной модели?
5. Какое слагаемое не может присутствовать в уравнении из системы для расчета параметров множественной регрессии?
a) 
b) 
6. Выберите из представленных моделей ту, которая является более качественной (n = 50)
a) R 2 = 0,85, m = 4
b) R 2 = 0,92, m = 5
c) R 2 = 0,90, m = 3
d) R 2 = 0,89, m = 3
7. Какая из ошибок спецификации наименее существенно влияет на качество модели?
a) невключение значимой переменной
b) включение незначимой переменной
c) неправильная спецификация
8. В какой модели параметры могут быть определены по МНК?
b) y = e α 0 + α 1 x 1 + α 2 x 2 + α 3 x 3 + ε
9. Какой размер имеет матрица корреляций?
10. Сумма диагональных элементов матрицы корреляции равна:
11. Какая из представленных формул предназначена для расчета 
a)
b)
c)
d)
12. Если мультиколлинеарность отсутствует, то определитель матрицы, составленной из коэффициентов корреляции независимых переменных, равен:
c) числу независимых переменных
13. На основе какого статистического критерия оценивается существенность добавления в модель переменной на основе сравнения коэффициентов детерминации?
a) t-критерий Стьюдента
b) F-критерий Фишера
c) критерий хи-квадрат
14. Какое значение коэффициента детерминации свидетельствует о том, что модель с 7-ю объясняющими переменными, основанная на анализе 30 единиц, статистически значима на 5%- уровне (F0,05;6;2 = 2,60)?
Список литературы
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.ЮНИТИ, 1998. – с. 515 – 590; 621 – 672.
2. Бородич С.А. Эконометрика: Учебное пособие. – Мн.: Новое знание, 2001. – с. 154 – 191; 271 – 280
3. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – XIV, с. 134 – 200
4. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – с. 82 – 100; 108 – 115; 124 – 130; 243 — 256
5. Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 2001. с. 83 – 89
6. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. 2-е изд. – М.: Дело, 1998. – с. 43 – 69; 74 – 90
7. Практикум по эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с. 49 – 105
8. Теория статистики: Учебник / под редакцией Р.А. Шмойловой. – 3-е изд. – М.: Финансы и статистика, 1999. – с. 289 – 295
9. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с.90 – 175
Последнее изменение этой страницы: 2016-08-01; Нарушение авторского права страницы
- http://pandia.ru/text/80/109/44488-5.php
- http://ekonomistu5.ru/uchebnye-materialy-po-ekonomike/linejnye-regressionnye-modeli-s-atributivnymi-faktorami
- http://infopedia.su/8xc14a.html