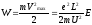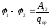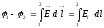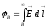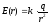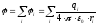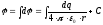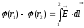Теория, объясняющая электрические свойства тел наличием в них электронов и их движением, носит название электронной теории. Эта теория очень просто и наглядно объясняет многие электрические явления; и поэтому при изучении электричества целесообразно с самого же начала ввести электронные представления. Разберем с этой точки зрения некоторые опыты, описанные выше.
В § 2 мы видели, что через металлы и другие проводники заряды могут легко переходить с одного тела на другое. Это значит, что в проводниках электрические частицы могут свободно перемещаться. И обратно: всякое тело, в котором электрические частицы могут легко перемещаться, должно оказаться хорошим проводником. Наоборот, из того факта, что стекло плохо проводит электричество, мы можем заключить, что внутри стекла (и других диэлектриков) перемещение электрических частиц от одного места к другому весьма затруднено. В хорошо проводящих растворах, например в растворах поваренной соли, легко перемещаются как положительные, так и отрицательные ионы. В металлах же ионы передвигаться не могут, и единственными переносчиками заряда в металлах являются электроны. Эти электроны, свободно перемещающиеся по металлу, называют свободными электронами или электронами проводимости.
Когда мы заряжаем какое-либо тело, то мы создаем на нем либо недостаток, либо избыток электронов по сравнению с их нормальным числом, при котором тело не заряжено. При этом электроны заимствуются у какого-либо другого тела или удаляются из тела, но отнюдь не уничтожаются и не создаются вновь. Таким образом, явление зарядки и разрядки тел сводится к перераспределению электронов без изменения общего числа их.
Мы знаем, что при соединении заряженного проводника с незаряженным заряд распределяется между обоими телами. С электронной точки зрения это происходит следующим образом. Если первое тело заряжено отрицательно, то электроны под действием взаимного отталкивания переходят на второе тело. Если же первое тело заряжено положительно, то оно притягивает к себе электроны второго тела. В обоих случаях заряд будет уменьшаться на первом теле и увеличиваться на втором до тех пор, пока вновь не наступит равновесие.
Наконец, мы видели (§ 4), что положительные и отрицательные заряды компенсируют друг друга, так что, соединяя равные по модулю разноименные заряды, мы получаем отсутствие заряда. С электронной точки зрения это очевидно: соединяя два проводника, в одном из которых не хватает стольких же электронов, сколько их содержится в избытке в другом, мы получим нормальное число электронов в каждом из проводников, т. е. каждый из проводников окажется незаряженным. Появление положительных и отрицательных зарядов при электризации тел трением представляет более сложный процесс, в деталях еще не вполне выясненный; но и в этом случае дело сводится именно к разделению зарядов, а не к образованию их.
© 2019 Научная библиотека
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
В металлах содержится большое количество электронов. Совокупность всех электронов образует «электронный газ». К «электронному газу» полностью применимы законы идеального газа.
Носителями тока в металлах являются свободные электроны, т. е. Электроны, слабо связанные с ионами кристаллической решетки металлов. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком П. Друде и разработанной в последствии нидерландским физиком Х. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории. Поэтому: электрический ток в металлах – направленное движение электронов, а не ионов (опыт Рикке: при длительном пропускании тока не наблюдалось взаимного проникновения вещества).
Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. Итак:
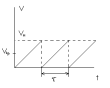
Электроны в металлах совершают хаотичное (тепловое) движение со скоростью 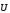
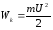
Эта энергия равна 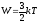
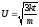
В обычных условиях — порядок скорости приблизительно 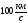

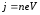
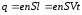
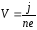

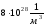
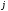
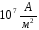
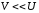
Казалось бы, что полученные результаты противоречат факту практически мгновенной передачи электрических сигналов на большие расстояния. Дело в том, что замыкание цепи влечет за собой распространение электрического поля со скоростью света. И через время 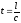
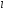
Объяснение закона Ома с точки зрения классической электронной теории.
Пусть в металлическом проводнике существует электрическое поле с напряженностью 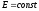
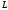

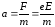
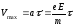
где 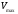
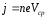
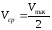
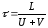
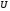
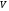
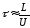
Плотность тока в металлическом проводнике:
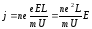
Коэффициент пропорциональности между 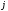
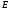
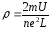
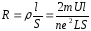
Объяснение закона Джоуля-Ленца с точки зрения классической электронной теории
Температура определяется энергией ионов металла. Электроны при столкновении с ионами отдают энергию, следовательно, температура повышается. К концу свободного пробега электрон под действием поля приобретает дополнительную энергию:
Один электрон в одну секунду может отдать энергию:
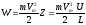
где Z-число столкновений.
В объеме за время t выделяется теплота:
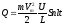
приводим к виду:
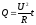
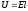
Следовательно, закон Джоуля-Ленца был доказан классической теорией.
Металл обладает как электропроводностью, а так как электроны – газ, то и теплопроводностью. Электроны, перемещаясь в металле переносят не только электрический заряд, но и присущую им электрическую энергию.
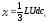
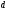
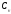
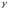
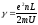
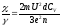
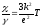
Из опыта 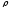
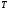
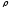
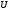
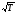
Квантовая теория сообщает, что электронный газ вообще не имеет теплоемкости.
Потенциальность электростатического поля. Скалярный потенциал. Неоднозначность скалярного потенциала и его нормировка. Потенциал точечного заряда, системы точечных зарядов и непрерывного распределения зарядов.
Потенциал электростатического поля.Способы описания электростатического поля:
Векторный (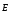
Скалярный (φ) – энергетическая характеристика.
φ (x,y,z) — потенциал электростатического поля, скалярная характеристика электростатического поля полностью (!) описывающая электростатическое поле
φ (x,y,z) 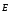
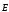
Определение Разностью потенциалов в двух точках (1) и (2) φ-φ2 — называется отношение A12 (работы по перемещению пробного единичного положительного заряда из (1) в (2), которую совершает поле) к заряду qпр.
интеграл может быть взят по любому пути соединяющему (1) и (2)
если (1) и (2) лежат на силовой линии, то в качестве линии, соединяющей (1) и (2) нужно взять силовую.
Понятие потенциала можно ввести для любого потенциального векторного поля. (потенциал гравит. силы, потенциал скорости и т.д.)
Потенциал Часто в качестве точки (2) выбирают точку, потенциал которой по определению = 0.
В теории – такая точка бесконечно удаленная: 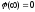
Замечание Это можно сделать лишь тогда, если заряды располагаются в ограниченной области пространства и их нет на бесконечности.
На практике 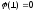
Потенциал электростатического поля в т. B(x,y,z) назыв.
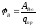
Расчетная формула:
Потенциал поля точечного заряда
Путь из точки B в ∞ может быть любым, т.к. поле потенциально. Наиболее удобно выбрать L вдоль радиуса вектора, проведенного из точечного заряда
El= Er = E(r); => 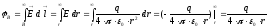
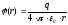
Т.к. поле точечного заряда фундаментально => для нахождения потенциала поля системы зарядов нужно применить принцип суперпозиций:
потенциал поля системы точечных зарядов равен сумме потенциалов, издаваемых в рассматриваемой точке каждым из зарядов.
а) потенциал поля системы точечных зарядов:
б) потенциал поля непрерывного распределения зарядов:
где dq = ρ∙dV — при объемном распределении заряда,
dq = σ∙dS — при поверхностном
dq = λ∙dl — при линейном.
Применение формулы поля точечного заряда и принципа суперпозиций составляет основу метода непосредственного интегрирования и позволяет рассчитать потенциал поля новой системы зарядов. Графически потенциал изображается в виде эквипотенциальных поверхностей и линий на которой он принимает постоянное значение = const.
Примеры расчета потенциала
Равномерно заряженная бесконечная нить. (Рис. 19)
Дано: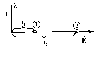
Т.к. поле нити имеет осевую симметрию и 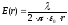
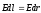
5. Электронная теория
5. Электронная теория
Электромагнитная теория Максвелла содержит уравнения, выражающие связь между измеряемыми в нашем обычном масштабе электромагнитными полями, с одной стороны, и электрическими зарядами и токами, с другой. Эти уравнения электродинамики, выведенные на основе обобщения результатов макроскопических экспериментов, были, несомненно, справедливыми для этого круга явлений. Но для детального описания электрической природы вещества и электромагнитных процессов, происходящих внутри атомов, описания процессов излучения и поглощения необходимо было экстраполировать уравнения Максвелла в область микромира и придать им форму, пригодную для описания явлений, происходящих в атоме. Это и было сделано одним из величайших создателей современной теоретической физики Г.А. Лоренцем.
В качестве отправной точки Лоренц принял гипотезу о дискретной структуре электричества. Он исходил из существования элементарных частиц электричества, которым дал общее название электронов, и предположил, что все вещества состоят из различных комбинаций этих элементарных частиц. То, что мы обычно называем электрически заряженным телом, это тело, содержащее в целом большее число частиц, несущих заряд одного знака, чем частиц, обладающих зарядом противоположного знака. Электрически же нейтральное тело содержит одинаковое число частиц разного знака. Само собой разумеется, что в материальных телах, т е. в макроскопических, число таких заряженных частиц всегда чрезвычайно велико. Согласно этой точке зрения, электрический ток, текущий по проводнику, обусловлен перемещением большого числа электронов, содержащихся в этом проводнике, а само явление проводимости объясняется некоторой свободой движения электронов в проводящем веществе и возможностью их перемещения под действием внешнего электрического поля. Изоляторы же, напротив, характеризуются отсутствием этой свободы, в них каждый электрон имеет некое положение равновесия и может смещаться из этого положения лишь на очень малые расстояния. Каждый из электронов создает свое электромагнитное поле, и наблюдаемые и измеряемые нами обычно поля не что иное, как средние статистические суммы элементарных полей, создаваемых чрезвычайно большим числом отдельных электронов, входящих в состав всех материальных тел. Как это часто бывает, среднее суммарное поле подчиняется весьма простым законам. Эти законы, записанные в математической форме, будут просто уравнениями, которые связывают непосредственно наблюдаемые макроскопические поля с электрическими зарядами и токами. Более смелая, чем теория Максвелла, теория Лоренца пыталась описать микроскопические электромагнитные явления и с их помощью в результате усреднения получить законы, которым подчиняются крупномасштабные макроскопические явления. Лоренц пытался определить электромагнитные поля, заряды и токи в каждой точке пространства, в каждый момент времени, причем не только в пространстве между зарядами, но и внутри самих электронов. Он предположил, что все микроскопические величины, такие, как поля, заряды, токи подчиняются уравнениям того же вида, что и макроскопические уравнения Максвелла, с той лишь разницей, однако, что в них уже не остается места для различия полей и соответствующих индукций, а заряды и токи оказались зависящими от самой структуры электричества. Можно показать, что, усредняя микроскопические величины, из уравнений Лоренца можно получить систему уравнений Максвелла. При этом выясняется различие между полями и индукциями. Таким образом, электромагнитная теория Максвелла оказывается теорией «крупномасштабных» электромагнитных полей, являющихся среднестатистической суммой элементарных или мелкомасштабных полей, описываемых теорией Лоренца.
Электронная теория, основные моменты которой мы только что кратко изложили, привела к серьезным успехам и позволила предсказать и объяснить большое число новых явлений. Она раскрыла физический смысл законов дисперсии, уже полученных к тому времени с помощью других теорий. Кроме того, и это несомненно было одним из крупных ее успехов, она позволила точно предсказать нормальный эффект Зеемана, т е. расщепление спектральных линий атомов под действием магнитного поля.
Экспериментальное подтверждение этого явления изменения частоты испускаемого атомами света под действием внешнего магнитного поля явилось замечательным подтверждением электронной теории. Стало понятно, что частицы, с движением которых связано излучение, есть не что иное, как отрицательные электроны, и, таким образом, было доказано существование их внутри вещества. Это было крупным успехом теории Лоренца. В общем, можно сказать, что электронная теория удовлетворительно объяснила все явления, в которых электрические и магнитные поля так или иначе влияют на условия излучения, распространения и поглощения света. К ним относится, например, явление вращения плоскости поляризации в магнитном поле (эффект Фарадея), которое в свете теории Лоренца можно рассматривать просто как обратный эффект Зеемана, а также явления двойного лучепреломления, вызванного электрическим или магнитным полем. Во всех этих областях, составляющих электро– и магнитооптику, теория Лоренца сыграла большую роль.
Электронная теория, казалось, ответила также на важный вопрос, что является источником излучения, испускаемого веществом. Согласно уравнениям Лоренца, электрон, движущийся прямолинейно и равномерно, полностью переносит с собой свое электромагнитное поле. Следовательно, в этом случае излучения энергии в окружающее пространство не происходит. Но если электрон движется с ускорением, то он излучает электромагнитные волны, и энергия, теряемая им в результате излучения, пропорциональна квадрату ускорения.
Излучение электромагнитных волн переменным током легко объяснить с точки зрения электронной теории, если учесть, что ток представляет собой громадное число периодически колеблющихся электронов. Сразу становится ясно, почему ток может излучать энергию. Понятным становится также излучение волн Герца токами в открытых контурах, такими, например, как ток, текущий в передающей антенне радиовещательных станций. Таким образом, мы возвращаемся к теории излучения волн Герца, основанной на уравнениях Максвелла.
Рассматривая излучение отдельных ускоренно движущихся электронов, теория Лоренца позволяет узнать первопричину излучения, понять, где находится источник излучения, испускаемого веществом. Следовательно, эта теория должна была бы в принципе объяснить возникновение электромагнитных волн в масштабе атома и показать, например, каким образом атомные спектры связаны с движением внутриатомных электронов. Электронная теория столкнулась с большими трудностями при попытке объяснить возникновение атомных спектров. Но вначале казалось, что эта теория ускорительных волн позволяет дать полное и исчерпывающее объяснение процессам испускания излучения веществом. И известное явление, заключающееся в возникновении рентгеновских лучей при резком торможении электронов на антикатоде, служило неопровержимым доказательством справедливости этой теории.
Несмотря на первые блестящие успехи, электронная теория оказалась не в состоянии объяснить явления в масштабе атома. При попытке рассмотреть вопрос о термодинамическом равновесии вещества и излучения на основании уравнений Лоренца возникают трудности, которых можно избежать лишь вводя совершенно новые представления квантовой теории. С другой стороны, для объяснения излучения атомов с точки зрения электронной теории приходится предположить, что в нормальном состоянии внутриатомные электроны неподвижны. В противном случае, двигаясь под действием кулоновских сил внутри чрезвычайно малой области пространства, они обладали бы отличным от нуля ускорением и должны были бы непрерывно терять энергию в виде электромагнитного излучения, что противоречит основному положению об устойчивости атома. Развитие наших знаний об атоме привело нас, как мы видели, к планетарной модели, исходящей из предположения о непрерывном движении электронов-планет. И тут возникло явное противоречие между теорией ускорительных волн и идеей стабильного атома. Разрешение этого противоречия может быть получено только с помощью введения новых, квантовых представлений (теория Бора).
На этих нескольких примерах, которые при желании можно было бы умножить, видно, что электромагнитная теория, дополненная и развитая Лоренцом, который учел дискретную структуру электричества, хотя и блестяще объяснила большое число различных явлений, столкнулась тем не менее с серьезными трудностями при попытке объяснить экспериментальные факты, относящиеся к атомному миру. Эти трудности можно было преодолеть только привлечением совершенно новых представлений, понятий и идей, в корне отличных от понятий и идей, называемых ныне классическими, на которых покоится электромагнитная теория.
Электронная теория дисперсии
Лекция «Взаимодействие электромагнитных волн с веществом»
2.Электронная теория дисперсии
3.Поглощение света. Закон Бугера
4.Излучение Вавилова- Черенкова
Дисперсия света
Дисперсия – это зависимость показателя преломления среды от частоты или длины волны. Более физично надо сказать, что дисперсия это зависимость фазовой скорости от частоты.
Следствием дисперсии является разложение призмой белого света в спектр. Данное явление впервые обнаружил Ньютон в 1672г. Угол отклонения Д лучей зависит от преломленного угла призмы Р и показатель преломления n. В призме наиболее сильно отклоняются фиолетовые лучи, а наибольшее слабо– красное. Следовательно, угол отклонения зависит от длины волны света.
D=р(n-1)
Призма, как и дифракционная решетка, является спектральным прибором, но в дифракционной решетке наиболее сильно отклоняются красные лучи. При помощи дифракционной решетки непосредственно определять длину волны падающего света. Призма же дает лишь зависимость угла отклонения от длины волны. Отношение называется дисперсией вещества. Она показывает, как быстро изменяется показатель преломления среды с изменением длины волны. Чем больше длина волны, тем меньше n; или чем больше частота, тем больше n.
Д= (1)
В формуле (1) при уменьшении длины волны увеличивается показатель преломления и соответственно увеличивается дисперсия. Такое поведение дисперсии называется нормальной. Вблизи линий и полос поглощения с уменьшением λ, показатель преломления уменьшается, соответственно уменьшается Д и такая дисперсия называется нормальной.
На явлении нормальной дисперсии основана работа спектрометров.
Электронная теория дисперсии
При изучении электромагнитной природы световых волн Максвеллом, им была получена формула, связывающая оптические, магнитные и электрические свойства среды.
(1) — формула Максвелла
Для видимого спектра для всех длин волн магнитная проницаемость µ, µ=1, а это значит, что показатель преломления , так как ε считается . На самом деле n зависит от частоты или λ, то есть электромагнитная теория Максвелла не объясняет явление дисперсии. Трудность объяснения дисперсии с точки зрения теории Максвелла устраняется в электронной теории дисперсии Лоренца. В теории Лоренца дисперсия рассматривается как результат взаимодействия электромагнитной волны с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания под действием переменного электрического поля.
Рассмотрим электронную теорию дисперсии и предположим, что электрическая проницаемость зависит от частоты проницаемости
χ- электрическая восприимчивость вещества
где р — вектор мгновенной поляризации
ε— диэлектрическая проницаемость вакуума
Е- напряженность электрического поля
(2)
(3)
Мы будем рассматривать прозрачный диэлектрик, в котором поляризуются электроны, то есть мы будем рассматривать электронную поляризацию. Электронная поляризация, то есть вынужденные колебания электронов под действием падающей электромагнитной волны будет играть преобладающую роль по сравнению со всеми другими видами поляризации, так как частота падающего света приблизительно 10 15 Гц, то это слишком большая частота, чтобы поляризовать атомы в молекулы. В первом приближении можно считать, что вынужденные колебания совершает только самый внешний электрон. Этот электрон наиболее слабо связан с ядром атома и поэтому под действием оптической электромагнитной волны. Он начинает совершать вынужденные колебания. Внешний электрон в атоме называется оптический электрон, приобретает наведенный дипольный момент, который определяется формулой (4)
(4)
е— заряд электрона
х – смещение электрона
Р — вектор мгновенной поляризации и р- наведенный дипольный момент связаны между собой формулой (5); n— концентрация атомов в диэлектрике. Тогда формула (3) с учетом формул (4), (5) запишется как
(6)
Падающая световая волна описывается выражением E=Ecoswt
E— амплитудное значение напряженности электрического поля. Эта световая волна создает внешнюю вынуждающую силу, которая будет периодическим
Тогда запишем все силы, движущие на электрон и найдем равнодействующую этих сил.
(8)
Формула (8) можно переписать в виде:
(9)
Так как мы рассматриваем прозрачный диэлектрик, то мы предполагаем, что затухание световых волн при прохождении через диэлектрик будет крайне незначительно, а это значит, что γ ≈→0 следовательно уравнение (9) можно записать как:
(9а)
Решением уравнения (9а) получено нами в классической механике и называется уравнение вынужденного колебания, его решением будет выражение
А- амплитуда незатухающего колебания
(11)
m- масса электрона
w— собственная частота внешнего электрона
w- частота падающей электромагнитной волны
Подставим в уравнение (6) формулу (10), (11)
(12)
Формула (12) описывает явления электронной дисперсии учитывающей колебания внешнего электрона. Если усложнить рассмотрение, то есть рассмотрим поляризацию не только внешнего электрона, но и всех имеющихся электрических зарядов, то формула, выражающая дисперсию примет вид:
(13)
N-число разных электрических зарядов
Формула (13) отражает явление дисперсии в наиболее общем виде. Рассмотрим дисперсию для газов, у которых n≈1. Будем работать с (12)
(14) — показатель преломления в газах
Проанализируем графически формулу (12), то есть рассмотрим, как изменится показатель преломления от частоты, падающей электромагнитной волны.
Рассмотрим изменение частоты внешней электромагнитной волны от w=0, w= w
в формуле (12) n 2 >1. При росте частоты от 0 до w знаменатель формулы (12) уменьшится, сама дробь увеличится, соответственно увеличится n. Он больше 1, то есть с ростом w до w увеличиться n среды, следовательно, наблюдается нормальная дисперсия. В точке w= w происходит разрыв функции и . При частоте w> w второе слагаемое в формуле (12) идет со знаком «- » и, следовательно, n 2
Объяснить с точки зрения электронной теории как возникает электрические заряды.
Вещество можно ионизировать. , приложив к нему достаточно сильное электрическое поле. Электроны имеют сравнительно малую массу, и во многих веществах совсем нетрудно «отрываются» от атомов таким полем. Атом, в котором недостает электронов, уже не уравновешивается по количеству зарядов, т. к. протоны в ядре остались нетронутыми, и общий заряд атома становится положительным. Такой атом называется положительным ионом, но это состояние неустойчиво. Как ты знаешь, разноименные заряды притягиваются друг к другу. Поэтому положительный ион «старается» притянуть к себе все, что окажется поблизости отрицательного — первый попавшийся электрон. Захвати его к себе, атом снова становится нейтральным и успокаивается. Так же можно в «запихнуть в атомную оболочку излишний электрон, и тогда атом превращается в отрицатеьлный ион. Это состояние тоже неустойчиво, и лишний электрон при первой же возможности выбрасывается из атома прочь.
Кроме того, в некоторых веществах имеются т. н. свободные заряды, т. е. частицы, не занятые в атомах, а блуждающие между ними хаотично, как молекулы в газе. Прикладывая электрическое поле к такому веществу, мы можем без труда «растащить» эти свободные заряды в разных направлениях, и тогда они скапливаются в избытке на концах предмета — с одной стороны электроны, с другой протоны. Стоит только убрать поле снова, как эти заряды быстро распределяются снова по всему объему предмета. Такие вещества называются «проводниками», т. к. содержат много частиц, способных свободно перемещаться между атомами и переносить свои заряды с места на место.
Объяснение закона Джоуля-Ленца с точки зрения классической электронной теории
Температура определяется энергией ионов металла. Электроны при столкновении с ионами отдают энергию, следовательно, температура повышается. К концу свободного пробега электрон под действием поля приобретает дополнительную энергию:
Один электрон в одну секунду может отдать энергию:
;
где Z-число столкновений.
В объеме за время t выделяется теплота:
;
приводим к виду:
, где .
Следовательно, закон Джоуля-Ленца был доказан классической теорией.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 9491 — 

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Как объяснить с точки зрения электронной теории
Современное представление электрического тока
На сегодняшний день считается, что электрический ток это направленное движение заряженных частиц — то есть движение электронов. В любом учебнике описано классическое понятие электрического тока, приводить его не имеет смысла. В это понятие не укладываются некоторые электрические явления и примеры.
1. Не имеет решения с точки зрения классического определения электрического тока следующая задача. Ток проходя через свинцовый предохранитель пережигает его. Найти скорость движения электронов в предохранителе. Нам дано: материал из которого сделан предохранитель — свинец. В справочниках мы можем посмотреть температуру плавления свинца Тпл знаем комнатную температуру при которой находится предохранитель Тком. Разница этих температур и есть искомая температура на которую надо нагреть предохранитель Тиск=Тпл-Тком
Где: m — масса предохранителя, C — удельная теплоёмкость свинца, l — плавление свинца.
Соответственно ту же работу Q1=Q совершают и электроны несущие электрический ток.
Где: mэ — масса электрона, V — скорость электрона, k — количество электронов.
Зная, что по классическому определению тока в процессе участвует только один электрон от каждого атома, то k-количество атомов свинца в предохранителе. При решении этой задачи V получается просто запредельная. Учитывая то, что электроны движутся по касательной к ядру атома, а не попадают в него перпендикулярно. Можно сделать предположение, что всё таки электрический ток это не движение электронов, а что то другое.
2. Явление пьезоэффекта трудно объяснить с точки зрения электрического тока. Невозможно объяснить как с механическое воздействие на объект вызывает электрический ток. И обратный процесс, электрический ток деформирует объект.
3. В промышленном производстве используется электросварка. При начале сварки в момент контакта электрода со свариваемым предметом, когда электрическая дуга ещё не зажглась. По сварочным кабелям течёт максимальный электрический ток. Так вот в этот короткий момент кабели начинают двигаться-дёргаться. Объяснить это явление с точки зрения классической теории электрического тока также невозможно.
4. Кроме того, невозможно объяснить явление статического электричества. При натирании шерсти янтарём и янтарь и шерсть являются диэлектриками.
Возможно электрический ток это не упорядоченное движение электронов, а упорядоченное движение ядер атомов вещества которое проводит электрический ток.
Попытаемся обосновать это предположение. Пусть электрический ток это упорядоченное колебание ядер атомов проводника.
При отсутствии электрического тока ядро покоится в центре атома, а при воздействии электрического тока начинает вращаться. Причём если ток течёт по проводнику от вас, то ядро вращается по часовой стрелке, а при течении тока на вас, против часовой. Эта гипотеза легко объясняет такое явление как магнетизм. .
Объяснение электризации
В § 8-а мы рассмотрели строение атома (положительно заряженное ядро и электронные оболочки) и строение металлов (положительно заряженные ионы и электронный газ). Это позволит нам объяснить явление электризации. Сделаем это.
 |
При трении тел друг о друга «трутся» именно электронные оболочки атомов, из которых тела состоят. А так как электроны слабо связаны с ядрами атомов, то электроны могут отделяться от «своих» атомов и переходить на другое тело. В результате на нём возникает избыток электронов (отрицательный заряд), а на первом теле – недостаток электронов (положительный заряд).
Итак, электризация трением объясняется переходом части электронов от одного тела к другому, в результате чего тела заряжаются разноимённо. Поэтому тела, наэлектризованные трением друг о друга, всегда притягиваются (см. § 8-б). Но, кроме электризации трением, существует электризация индукцией (лат. «индукцио» – наведение). Рассмотрим её на опыте:
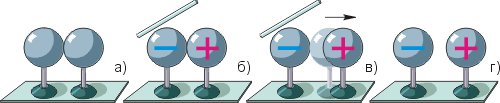 |
В начале опыта имеются два металлических шара, которые касаются друг друга (а). К одному из них подносят, не касаясь его, заряженную стеклянную палочку (б), после чего второй шар отодвигают (в). Теперь палочку можно убрать, – шары будут разноимённо заряжены (г).
 |
Объясним этот опыт с точки зрения электронно-ионной теории.
Сначала металлические шары не были заряжены. Это значит, что электронный газ присутствовал в шарах в равных количествах (а). Поскольку палочка стеклянная, мы считаем её заряд положительным (см. § 8-б). Она притягивает отрицательно заряженные частицы – электроны. В результате электронный газ «перетекает» в левую часть левого шара, и в этом месте образуется избыток отрицательного заряда (б).
Все положительные ионы металла прочно связаны друг с другом (они и есть металл), поэтому никуда не «перетекают». Значит, во всех остальных частях шаров возникает недостаток электронов, то есть положительный заряд. И если в этот момент, не убирая палочку, раздвинуть шары (в) и лишь затем убрать её, шары останутся разноимённо заряженными (г).
Итак, электризация индукцией объясняется перераспределением электронного газа между телами (или частями тела), в результате чего тела (или части тела) заряжаются разноимённо. Однако возникает вопрос: все ли тела поддаются электризации индукцией? Можно проделать опыты и убедиться, что пластмассовые, деревянные или резиновые шары можно легко наэлектризовать трением, но невозможно индукцией. Объясним это.
Электроны в резине, древесине и во всех пластмассах не являются свободными, то есть не образуют электронного газа, который может перетекать в другие тела. Поэтому для электризации тел из этих веществ необходимо прибегнуть к их трению, способствующему отделению электронов от «своих» атомов и переходу на другое тело.
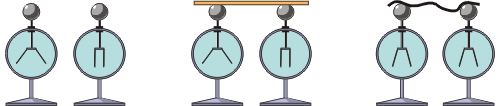 |
Итак, по электрическим свойствам все вещества можно разделить на две группы. Диэлектрики – вещества, не имеющие свободных заряженных частиц и потому не проводящие заряд от одного тела к другому. Проводники – вещества со свободными заряженными частицами, которые могут перемещаться, перенося заряд в другие части тела или к другим телам. Это иллюстрирует рисунок с электроскопами, пластмассовой линейкой и металлической проволокой (см. выше).
Теория Друде-Лоренца. Электронная теория проводимости металлов
Созданием классической электронной теории проводимости металлов наука обязана прежде всего Джозефу Джону Томсону, который в 1897 г. открыл электрон, а в 1898 г. определил его заряд. Исследуя прохождение электрического тока в разреженных газах, он установил, что это поток отрицательно заряженных частиц, масса которых приблизительно в 1837 раз меньше массы атома обычного водорода. Пауль Друде в 1900 г. положил начало классической теории проводимости металлов, которую развил в 1904 г. Гендрик Лоренц.
В основу теории Друде-Лоренца положена кинетическая теория газов, закономерности поведения идеального газа. Считается, что свободные электроны (электроны, потерявшие связь со «своими» атомами) в металлах подчиняются законам идеального газа.
Скорость хаотического движения свободных электронов в металлах можно определить, если воспользоваться представлением о свободных электронах, как об одноатомном электронном газе. В самом деле, средняя кинетическая энергия одноатомной молекулы идеального газа согласно молекулярно-кинетической теории
где k — постоянная Больцмана; T — температура по шкале Кельвина; m — масса электрона, а u̅ — средняя квадратическая скорость движения свободных электронов.
| Томсон Джозеф Джон (1856 — 1940) — английский физик. В 1906 г. стал лауреатом Нобелевской премии по физике за теоретические и экспериментальные исследования прохождения электрического тока в газах. |
| Друде Пауль Карл Людвиг (1863 — 1906) — немецкий физик. В 1900 г. положил начало электронной теории проводимости металлов. |
Для комнатной температуры (300 К) скорость хаотического движения электронов около 110 км/с. Тем не менее, хаотическое движение электронов не обусловливает возникновения тока в проводнике — направленного перемещения заряженных частиц.
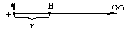
Если же теперь в проводнике площадью поперечного сечения S и длиной l образовать однородное электрическое поле с напряженностью E̅, то на каждый свободный электрон будет действовать сила F = eE, где e — заряд электрона (рис.7.1). Под действием таких сил на хаотическое движение свободных электронов будет накладываться направленное их перемещение, что и образует ток в проводнике (так движется рой пчел или мошек под действием ветра).
Средняя скорость направленного движения электронов v̅, образующих ток, крайне мала по сравнению со средней скоростью u̅ их хаотического движения, поскольку электроны часто сталкиваются с ионами кристаллической решетки, отдавая им практически всю энергию, которую приобрели вследствие направленного движения (при столкновениях теряется скорость направленного движения электронов, а скорость их хаотического движения сохраняется).
Поскольку электронное поле в проводнике распространяется со скоростью света (около 3 • 10 8 м/с), то свободные электроны в проводнике направленно начинают двигаться практически одновременно, не прекращая своего хаотического движения.
| Рис. 7.1. Образование тока в проводнике |
Средняя длина свободного пробега электрона λ̅ (расстояние, которое проходит электрон между двумя последовательными столкновениями с ионами кристаллической решетки) имеет такой же порядок, как и постоянная кристаллической решетки (приблизительно 10 -8 см).
На пути свободного пробега электрон движется с ускорением, которое можно определить по второму закону динамики Ньютона
Очевидно, что максимальная скорость электрона в момент его столкновения с ионом
где Δt — время свободного пробега.
Если иметь в виду, что в наиболее общей форме закон Ома j = σE = (1 / ρ) • E, то можно сделать вывод, что
формула j = (e 2 nλ̅ / 2mu̅) • E выражает закон Ома с точки зрения электронной теории. Материал с сайта http://worldofschool.ru
| Лоренц Гендрик Антон (1853 — 1928) — нидерландский физик, создатель электронной теории и электродинамики движущихся сред. В 1902 г. вместе с Питером Зиманом получил Нобелевскую премию за исследование влияния магнитных полей на излучение. |
Из этого закона можно найти значение удельной электропроводимости и удельного сопротивления:
Тщательные экспериментальные исследования показали, что закон Ома, полученный на основании классических представлений, довольно хорошо выполняется лишь при обычных и высоких температурах. При низких температурах приходится вносить поправки. Так, в законе Ома есть коэффициент ½ = 0,5. Лоренц ввел поправку для коэффициента — он установил его равным 0,75. Но и это не спасло классическую электронную теорию.
Позже была создана квантовая теория проводимости металлов, но и она оказалась приблизительной, хотя и точнее описывала явления.
Взаимодействие образующих ток электронов с ионами кристаллической решетки является причиной электрического сопротивления. Отдавая ионам часть своей энергии, электроны увеличивают амплитуду их колебаний — повышается температура металла.
Физические теории и закономерности всегда носят приблизительный характер, однако с развитием науки они все лучше описывают явления окружающего мира.
- http://studfiles.net/preview/5623519/page:3/
- http://fis.wikireading.ru/109
- http://megaobuchalka.ru/3/18315.html
- http://otvet.mail.ru/question/72968223
- http://studopedia.ru/5_103783_ob-yasnenie-zakona-dzhoulya-lentsa-s-tochki-zreniya-klassicheskoy-elektronnoy-teorii.html
- http://science-freaks.livejournal.com/893613.html
- http://questions-physics.ru/uchebniki/8_klass/obyasnenie_elektrizatsii.html
- http://worldofschool.ru/fizika/kondens/tv-tela/teoriya-drude-lorenca.-elektronnaya-teoriya-provodimosti-metallov