Объемный подход к измерению информации применяется в цифровых (компьютерных) системах хранения и передачи информации. В этих системах используется двоичный способ кодирования информации. При объемном подходе для определения количества информации имеет значение лишь размер (объем) хранимого и передаваемого кода. Объемный подход еще называют алфавитным подходом. Из курса информатики 8–9 классов вы знаете, что если с помощью i-разрядного двоичного кода можно закодировать алфавит, состоящий из N символов, то эти величины связаны между собой по формуле:
Число N называется мощностью алфавита. Например, если i = 2, то можно построить 4 двухразрядные комбинации из нулей и единиц, т. е. закодировать 4 символа. При i = 3 существует 8 трехразрядных комбинаций нулей и единиц (кодируется 8 символов):
| i=2: |
| i=3: |
Английский алфавит содержит 26 букв. Для записи текста нужны еще, как минимум, шесть символов: пробел, точка, запятая, вопросительный знак, восклицательный знак, тире. В сумме получается расширенный алфавит, мощностью в 32 символа.
Поскольку 2 5 =32, то все символы можно закодировать всевозможными пятиразрядными двоичными кодами от 00000 до 11111. Именно пятиразрядный код использовался в телеграфных аппаратах, появившихся еще в XIX веке. Телеграфный аппарат при вводе переводил английский текст в двоичный код, длина которого в 5 раз больше, чем длина исходного текста.
| В двоичном коде каждая двоичная цифра несет одну единицу информации, которая называется 1 бит. |
| Бит является основной единицей измерения информации. |
Длина двоичного кода, с помощью которого кодируется символ алфавита, называется информационным весом символа. В рассмотренном выше примере информационный вес символа расширенного английского алфавита оказался равным 5 битам.
Информационный объем текста складывается из информационных весов всех составляющих его символов. Например, английский текст из 1000 символов в телеграфном сообщении будет иметь информационный объем 5000 бит.
Алфавит русского языка включает 33 буквы. Если к нему добавить еще пробел и пять знаков препинания, то получится набор из 39 символов. Для его двоичного кодирования пятиразрядного кода уже не достаточно. Нужен, как минимум, 6-разрядный код. Поскольку 2 6 =64, то остается еще резерв для 25 символов (64-39=25). Его можно использовать для кодирования цифр, всевозможных скобок, знаков математических операций и других символов, встречающихся в русском тексте. Следовательно, информационный вес символов в расширенном русском алфавите будет равен 6 битам. А текст из 1000 символов будет иметь объем 6000 бит.
Если i- информационный вес символа алфавита, а К – число символов в тексте, записанном с помощью этого алфавита, то информационный объем текста (I) выражается формулой:
Идея измерения количества информации в сообщении через длину двоичного кода с этим сообщением принадлежит выдающемуся российскому математику Андрею Николаевичу Колмогорову. Согласно Колмогорову, количество информации, содержащееся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.
|
Для определения информационного веса символа полезно представлять себе ряд целых степеней двойки. Вот как он выглядит в диапазоне от 2 1 до 2 10 :
| i |
| 2 i |
Информационный вес символа из алфавита мощности N определяется по ближайшему значению во второй строке таблицы, не меньшему, чем N. Соответствующее значение i в первой строке равно информационному весу символа.
Пример. Определим информационный вес символа из алфавита, включающего в себя все строчные и прописные русские буквы (66); цифры (10); знаки препинания, скобки, кавычки (10). Всего получается 76 символов.
Поскольку 2 6 7 , следовательно, информационный вес символов данного алфавита равен 7 битам. Это означает, что все 76 символов можно закодировать семиразрядными двоичными кодами.
Из базового курса информатики вам известно, что в компьютерах используется двоичное кодирование информации. Для двоичного представления текстов в компьютере чаще всего применяется восьмиразрядный код. С помощью восьмиразрядного кода можно закодировать алфавит из 256 символов, поскольку 256=2 8 . В стандартную кодовую таблицу (например, ASCII), помещаются все необходимые символы: английские и русские буквы прописные и строчные, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр.
Более крупной единицей измерения информации является байт: 1 байт = 8 бит.
Информационный объем текста в памяти компьютер, измеряется в байтах. При использовании восьмиразрядного кода он равен количеству символов в записи текста
Одна страница текста на листе формата А4 кегля 12 с одинарным интервалом между строками (см. пример выше) в компьютерном представлении будет иметь объем 4000 байтов, так как на ней помещается примерно 4000 знаков.
Помимо бита и байта, для измерения информации используются и более крупные единицы:
1Кб (килобайт) = 2 10 байт=1024 байта;
1Мб (мегабайт) = 2 10 Кб=1024 Кб;
1Гб (гигабайт) = 2 10 Мб=1024 Мб;
1Тб (терабайт) = 2 10 Гб=1024 Гб.
Объем той же страницы текста будет равным приблизительно 3,9Кб. А книга из 500 таких страниц займет в памяти компьютера примерно 1,9 Мб.
В компьютере любые виды информации: тексты, числа, изображения, звук — представляются путем двоичного кодирования
Объем любой информации, выраженный в битах, равен количеству двоичных разрядов в ее представлении в памяти компьютера
| Измерение информации – объемный (алфавитный) подход | ||||
| На бумажных носителях | На цифровых носителях и в технических системах передачи информации | |||
| Объем текста измеряется в знаках | Объем информации равен размеру двоичного кода Основная единица:1 бит – один разряд двоичного кода | |||
| Информационный вес символа (i бит) из алфавита, мощностью N , определяется из уравнения: 2 i = M.Где N ≤ M – ближайшая сверху целая степень двойки | Информационный объем текста (I), содержащего К символов I=K×i бит | |||
| Производные единицы | ||||
| 1 б= 8 бит | 1 Кб=1024 б | 1 Мб=1024 Кб | 1 Гб=1024 Мб | 1 Тб=1024 Мб |
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8019 — 

193.124.117.139 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
При всем многообразии подходов к определению понятия информации, с позиции измерения информации нас будут интересовать два из них: определение К. Шеннона, применяемое в математической теории информации (содержательный подход), и определение А. Н. Колмогорова, применяемое в отраслях информатики, связанных с использованием компьютеров (алфавитный подход).
Содержательный подход
По Шеннону, информация — уменьшение неопределенности наших знаний.
Неопределенность некоторого события — это количество возможных исходов данного события.
Так, например, если из колоды карт наугад выбирают карту, то неопределенность равна количеству карт в колоде. При бросании монеты неопределенность равна 2.
Содержательный подход часто называют субъективным, так как разные люди (субъекты) информацию об одном и том же предмете оценивают по-разному.
Но если число исходов не зависит от суждений людей (случай бросания кубика или монеты), то информация о наступлении одного из возможных исходов является объективной.
Если сообщение уменьшило неопределеность знаний ровно в два раза, то говорят, что сообщение несет 1 бит информации.
1 бит — объем информации такого сообщения, которое уменьшает неопределенность знания в два раза.
Рассмотрим, как можно подсчитать количество информации в сообщении, используя содержательный подход.
Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных (равновозможных) событий. Тогда количество информации i, заключенное в этом сообщении, и число событий N связаны формулой: 2 i = N. Эта формула носит название формулы Хартли. Получена она в 1928 г. американским инженером Р. Хартли.
Если N равно целой степени двойки (2, 4, 8, 16 и т.д.), то вычисления легко произвести «в уме». В противном случае количество информации становится нецелой величиной, и для решения задачи придется воспользоваться таблицей логарифмов либо определять значение логарифма приблизительно (ближайшее целое число, большее).
Например, если из 256 одинаковых, но разноцветных шаров наугад выбрали один, то сообщение о том, что выбрали красный шар несет 8 бит информации (2 8 =256).
Для угадывания числа (наверняка) в диапазоне от 0 до 100, если разрешается задавать только двоичные вопросы (с ответом «да» или «нет»), нужно задать 7 вопросов, так как объем информации о загаданном числе больше 6 и меньше 7 (2 6 2 7 )
Алфавитный подход
Алфавитный подход основан на том, что всякое сообщение можно закодировать с помощью конечной последовательности символов некоторого алфавита.
Алфавит — упорядоченный набор символов, используемый для кодирования сообщений на некотором языке.
Мощность алфавита — количество символов алфавита.
Двоичный алфавит содержит 2 символа, его мощность равна двум.
Сообщения, записанные с помощью символов ASCII, используют алфавит из 256 символов. Сообщения, записанные по системе UNICODE, используют алфавит из 65 536 символов.
С позиций computer science носителями информации являются любые последовательности символов, которые хранятся, передаются и обрабатываются с помощью компьютера. Согласно Колмогорову, информативность последовательности символов не зависит от содержания сообщения, алфавитный подход является объективным, т.е. он не зависит от субъекта, воспринимающего сообщение. Чтобы определить объем информации в сообщении при алфавитном подходе, нужно последовательно решить задачи:
-
Определить количество информации (i) в одном символо по формуле 2 i = N, где N — мощность алфавита -
Определить количество символов в сообщении (m) -
Вычислить объем инофрмации по формуле: V = i * m.
Например, если текстовое сообщение, закодированное по системе ASCII, содержит 100 символов, то его информационный объем составляет 800 бит.
Для двоичного сообщения той же длины информационный объем составляет 100 бит. В компьютерной технике бит соответствует физическому состоянию носителя информации: намагничено — не намагничено, есть отверстие — нет отверстия. При этом одно состояние принято обозначать цифрой 0, а другое — цифрой 1.
Единицы измерения информации
Вопросы для самоконтроля
-
Какие подходы к измерению информации вам известны? -
Какова основная единица измерения информации? -
Сколько байт содержит 1 Кб информации? -
Приведите формулу подсчета количества информации при уменьшении неопределенности знания. -
Как подсчитать количество информации, передаваемое в символьном сообщении?
В информатике используются различные подходы к измерению информации:
Содержательный подход к измерению информации. Сообщение – информативный поток, который в процессе передачи информации поступает к приемнику. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными Информация — знания человека ? сообщение должно быть информативно. Если сообщение не информативно, то количество информации с точки зрения человека = 0. (Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику)
Алфавитный подход к измерению информации не связывает кол-во информации с содержанием сообщения. Алфавитный подход — объективный подход к измерению информации. Он удобен при использовании технических средств работы с информацией, т.к. не зависит от содержания сообщения. Кол-во информации зависит от объема текста и мощности алфавита. Ограничений на max мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере. Поскольку 256=2 8 , то 1символ несет в тексте 8 бит информации.
Вероятностный подход к измерения информации. Все события происходят с различной вероятностью, но зависимость между вероятностью событий и количеством информации, полученной при совершении того или иного события можно выразить формулой которую в 1948 году предложил Шеннон.
Количество информации — это мера уменьшения неопределенности.
1 БИТ – такое кол-во информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза. БИТ- это аименьшая единица измерения информации
Единицы измерения информации: 1байт = 8 бит
1Кб (килобайт) = 2 10 байт = 1024 байт
1Мб (мегабайт) = 2 10 Кб = 1024 Кб
1Гб (гигабайт) = 2 10 Мб = 1024 Мб
В информатике, как правило, измерению подвергается информация, представленная дискретным сигналом. При этом различают следующие подходы:
-
структурный. Измеряет количество информации простым подсчетом информационных элементов, составляющих сообщение. Применяется для оценки возможностей запоминающих устройств, объемов передаваемых сообщений, инструментов кодирования без учета статистических характеристик их эксплуатации.
-
статистический. Учитывает вероятность появления сообщений: более информативным считается то сообщение, которое менее вероятно, т.е. менее всего ожидалось. Применяется при оценке значимости получаемой информации.
-
семантический. Учитывает целесообразность и полезность информации. Применяется при оценке эффективности получаемой информации и ее соответствия реальности.
Структурный подход к измерению информации
В рамках структурного подхода выделяют три меры информации:
-
геометрическая. Определяет максимально возможное количество информации в заданных объемах. Мера может быть использована для определения информационной емкости памяти компьютера; -
комбинаторная. Оценивает возможность представления информации при помощи различных комбинаций информационных элементов в заданном объеме. Комбинаторная мера может использоваться для оценки информационных возможностей некоторого системы кодирования; -
аддитивная, или мера Хартли. -
Геометрическая мера
Определяет максимально возможное количество информации в заданных объемах. Единица измерения – информационный элемент. Мера может быть использована для определения информационной емкости памяти компьютера. В этом случае в качестве информационного элемента выступает минимальная единица хранения – бит. Список самых распространенных более крупных единиц и соотношение между ними приведено ниже:
8 бит = 1 байт (сокращенно б или Б),
1024 Б = 1 килобайт (сокращенно Кб или К),
1024 К = 1 мегабайт (сокращенно Мб или М),
1024 М = 1 гигабайт (сокращенно Гб или Г).
Тогда, например, объем винчестера – 3 гигабайта; объем основной памяти компьютера – 32 мегабайта и т.д.
Пример 1. Пусть сообщение
5555 6666 888888
закодировано одним из специальных методов эффективного кодирования – кодирование повторений – и имеет вид:
5(4) 6(4) 8(6) .
Требуется измерить информацию в исходном и закодированном сообщениях геометрической мерой и оценить эффективность кодирования.
В качестве информационного элемента зададимся символом сообщения. Тогда:
I(исх.) = l(исх.) = 14 символов;
I(закод.) = l(закод.) = 12 символов,
где I(исх.), I(закод.) – количества информации, соответственно, в исходном и закодированном сообщениях;
l(исх.), l(закод.) – длины (объемы) тех же сообщений, соответственно.
Эффект кодирования определяется как разница между I(исх.) и I(закод.) и составляет 2 символа.
Очевидно, геометрическая мера не учитывает, какими символами заполнено сообщение. Так, одинаковыми по количеству информации, измеренной геометрической мерой, являются, например, сообщения «компьютер» и «программа»; а также 346 и 10В.
Комбинаторная мера
Оценивает возможность представления информации при помощи различных комбинаций информационных элементов в заданном объеме. Использует типы комбинаций элементов и соответствующие математические соотношения, которые приводятся в одном из разделов дискретной математики – комбинаторике.
Комбинаторная мера может использоваться для оценки информационных возможностей некоторого автомата, который способен генерировать дискретные сигналы (сообщения) в соответствии с определенным правилом комбинаторики. Пусть, например, есть автомат, формирующий двузначные десятичные целые положительные числа (исходное множество информационных элементов ). В соответствии с положениями комбинаторики, данный автомат генерирует размещения (различаются числа, например, 34 и 43) из 10 элементов (используются 10 цифр) по 2 (по условию задачи, формируются двузначные числа) с повторениями (очевидно, возможны числа, состоящие из одинаковых цифр, например, 33). Тогда можно оценить, сколько различных сообщений (двузначных чисел) может сформировать автомат, иначе говоря, можно оценить информационную емкость данного устройства: Рп(102) = 102 = 100.
Комбинаторная мера используется для определения возможностей кодирующих систем, которые широко используются в информационной технике.
Пример 1. Определить емкость ASCII-кода, представленного в двоичной или шестнадцатеричной системе счисления.
ASCII-код – это сообщение, которое формируется как размещение с повторениями:
-
для двоичного представления – из информационных элементов , сообщение длиной (объемом) 8 символов; -
для шестнадцатеричного представления – из информационных элементов , сообщение длиной (объемом) 2 символа.
Тогда в соответствии с положениями комбинаторики:
I(двоичное) = РП(28) = 28 = 256;
I(шестнадцатеричное) = РП(162) = 162 = 256,
где I(двоичное), I(шестнадцатеричное) – количества информации, соответственно, для двоичного и шестнадцатеричного представления ASCII-кода.
Таким образом, емкость ASCII-кода для двоичного и шестнадцатеричного представления одинакова и равна 256.
Следует отметить, что все коды постоянной длины формируются по правилам комбинаторики или их комбинациям.
В случае, когда сообщения формируются как размещения с повторениями из элементов алфавита мощности h и известно количество сообщений М, можно определить требуемый объем сообщения (т.е. его длину l) для того, чтобы в этом объеме представить все сообщения: l = log h М .
Например, есть 4 сообщения – a, b, c, d. Выполняется двоичное кодирование этих сообщений кодом постоянной длины. Для этого требуются 2 двоичных разряда. В самом деле: l = log 2 4 = 2.
Очевидно, комбинаторная мера является развитием геометрической меры, так как помимо длины сообщения учитывает объем исходного алфавита и правила, по которым из его символов строятся сообщения.
Особенностью комбинаторной меры является то, что ею измеряется информация не конкретного сообщения, а всего множества сообщений, которые могут быть получены.
Единицей измерения информации в комбинаторной мере является число комбинаций информационных элементов.
Эта мера предложена в 1928 году американским ученым Хартли, поэтому имеет второе название – мера Хартли. Хартли впервые ввел специальное обозначение для количества информации – I и предложил следующую логарифмическую зависимость между количеством информации и мощностью исходного алфавита:
где I – количество информации, содержащейся в сообщении;
l – длина сообщения;
h – мощность исходного алфавита.
При исходном алфавите ; l = 1; h = 2 и основании логарифма, равном 2, имеем
Данная формула даёт аналитическое определение бита (BIT — BInary digiT) по Хартли: это количество информации, которое содержится в двоичной цифре.
Единицей измерения информации в аддитивной мере является бит.
Пример 1. Рассчитать количество информации, которое содержится в шестнадцатеричном и двоичном представлении ASCII-кода для числа 1.
В соответствии с таблицей ASCII-кодов имеем: шестнадцатеричное представление числа 1 – 31, двоичное представление числа 1 – 00110001.
Тогда по формуле Хартли получаем:
для шестнадцатеричного представления I = 2log216 = 8 бит;
для двоичного представления I = 8 log22 = 8 бит.
Таким образом, разные представления ASCII-кода для одного символа содержат одинаковое количество информации, измеренной аддитивной мерой.
скачать
Подходы к измерению информации
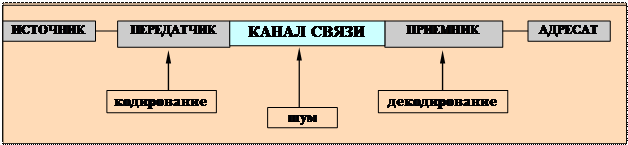
Общая схема передачи сообщения
Источник сообщения — человек или физический, технический и т.д. процесс. Сообщение может быть закодировано (шифр, преобразование человеческой речи в радио-сигнал, электромагнитные колебания, оптические сигналы и т.д.).
Ø От передатчика до приемника закодированный сигнал передается по каналу связи. В качестве носителя при передаче сообщения по каналу связи чаще всего используют:
w механические движения (механика)
w механическое давление жидкости или газа (гидравлика, пневматика)
w волны давления в жидкостях, газах, твердом теле (акустика)
w электрические токи и напряжения,
w электромагнитные волны (радио, свет).
Пропускная способность канала – количество передаваемой по каналу информации, измеряется в бит/с.
2.6. Измерения информации
Подходы к измерению информации
В информатике используются различные подходы к измерению информации:
Алфавитный (кибернетический, объемный) подход к измерению информациине связывает кол-во информации с содержанием сообщения. Кол-во информации зависит от объема текста и мощности алфавита.
Алфавит – конечное множество различных знаков, символов, для которых определена операция конкатенации (приписывания, присоединения символа к символу или цепочке символов); с ее помощью по определенным правилам соединения символов и слов можно получать слова (цепочки знаков) и словосочетания (цепочки слов) в этом алфавите.
Конечная последовательность букв алфавита называется словом.
Длиной некоторого слова называется число составляющих его символов.
N при алфавитном подходе называют мощностью алфавита. Информационная ёмкость каждого знака зависит от количества знаков в алфавите. Следовательно, каждый из N символов несёт i бит информации.
Остаётся подсчитать количество символов в тексте сообщения k.
Алфавитный подход является объективным способом измерения информации и подходит для работы технических устройств.
Минимальная мощность алфавита, пригодного для передачи информации, равна 2. Такой алфавит называется двоичным алфавитом. Информационный вес символа в двоичном алфавите легко определить. Поскольку 2 i = 2, то i = 1 бит. Итак, один символ двоичного алфавита несет 1 бит информации.
Например, основная физическая единица длины — метр. Но существуют миллиметр, сантиметр, километр. Расстояния разного размера удобно выражать через разные единицы. Так же обстоит дело и с измерением информации.
1 бит — это исходная единица.
Следующая по величине единица — байт. Байт вводится как информационный вес символа из алфавита мощностью 256. Поскольку 256 = 2 8 , то 1 байт = 8 бит.
Ограничений на max мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере. Поскольку 256=2 8 , то 1 символ несет в тексте 8 бит информации.
Пример: слово «мир» несет 24 бит информации.
Содержательный (энтропийный, вероятностный) подход к измерению информации. Этотподход основан на том, что факт получения информации всегда связан с уменьшением неопределенности (энтропии) системы. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными. Если сообщение не информативно, то количество информации с точки зрения человека = 0.
Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику.
Количество информации — это мера уменьшения неопределенности. В качестве меры неопределенности вводится энтропия Н, а количество информации равно:
I = Hapr – Haps
гдеHapr – априорная энтропия о состоянии исследуемой системы или процесса;
Haps – апостериорная энтропия.
Апостериори (от лат. aposteriori – из последующего) – происходящее из опыта (испытания, измерения). Априори (от лат. apriori – из предшествующего) – понятие, характеризующее знание, предшествующее опыту (испытанию) и независимое от него.
В случае, когда в ходе испытания имевшаяся неопределенность снята (получен конкретный результат, то есть Haps = 0), количество полученной информации совпадает с первоначальной энтропией.
Так, американский инженер Р. Хартли (1928 г.) процесс получения информации рассматривает как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определяет как двоичный логарифм N.
| Формула Хартли: H= log2N. |
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 » 6,644. То есть сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.
Приведем другие примеры равновероятных сообщений:
1. при бросании монеты: «выпала решка», «выпал орел»;
2. на странице книги: «количество букв чётное», «количество букв нечётное».
Определим теперь, являются ли равновероятными сообщения «первой выйдет из дверей здания женщина» и «первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
| Формула Шеннона: I = – ( p1 log2 p1 + p2 log2 p2 + . . . + pN log2 pN ), где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. N – количество сообщений |
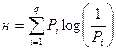 |
Легко заметить, что если вероятности p1, . pN равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
Задача1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков
1) всего шаров 50+25+25=100
2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4
Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно расcчитать по формуле
Задача2 : В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?
т.к. N = 16 шаров, то I = log2 N = log2 16 = 4 бит.
Алгоритмическое измерение информации [2]
Был предложен в 1965 году академиком А.Н. Колмогоровым. Алгоритмическая сложность некоторой последовательности данных определяется как минимальная длина вычислительного алгоритма, который мог бы воспроизвести заданную последовательность.
Например: слово 000000 – простое, слово 01010101 – более сложное, а слово, в котором 0 и 1 выбираются экспериментально при бросании монеты (1 – орел, 0 – решка), еще сложнее.
Компьютерная программа, печатающая первое слово, совсем простая; для получение второго слова нужна более сложная программа, которая будет печатать символ, противоположный предыдущему. Случайная последовательность, не обладающая никакими закономерностями, может быть напечатана программой, в которой каждый очередной символ будет печататься отдельным оператором. То есть длина такой программы будет близка к длине самой последовательности. Следовательно, любому сообщению можно приписать количественную характеристику, отражающую размер программы, которая позволяет ее воспроизвести.
| | | следующая лекция ==> | |
| Плавники выполняют разные функции. | | | Графические форматы. Аппаратное обеспечение компьютерной графики |
Дата добавления: 2016-05-25 ; просмотров: 7401 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Алфавитный (объемный) подход к измерению информации
Помимо описанного выше вероятностного подхода к измерению информации, состоящего в подсчете неопределенности исходов того или иного события, существует и другой. Его часто называют объемным, и он заключается в определении количества информации в каждом из знаков дискретного сообщения с последующим подсчетом количества этих знаков в сообщении.
Пусть сообщение кодируется с помощью некоторого набора знаков. Заметим, что если для данного набора установлен порядок следования знаков, то он называется алфавитом. Наиболее сложной частью работы при объемном измерении информации является определение количества информации, содержащейся в каждом отдельном символе: остальная часть процедуры весьма проста. Для определения информации в одном символе алфавита можно также использовать вероятностные методы, поскольку появление конкретного знака в конкретном месте текста есть явление случайное.
Самый простой метод подсчета заключается в следующем. Пусть алфавит, с помощью которого записываются все сообщения, состоит из M символов. Для простоты предположим, что все они появляются в тексте с одинаковой вероятностью (конечно, это грубая модель3, но зато очень простая). Тогда в рассматриваемой постановке применима формула Хартли для вычисления информации об одном из исходов события (о появлении любого символа алфавита):
Поскольку все символы “равноправны”, естественно, что объем информации в каждом из них одинаков. Следовательно, остается полученное значение I умножить на количество символов в сообщении, и мы получим общий объем информации в нем. Напомним читателям, что осмысленность сообщения в описанной процедуре нигде не требуется, напротив, именно при отсутствии смысла предположение о равновероятном появлении всех символов выполняется лучше всего!
Можно показать, что при любом варианте кодирования
(чем экономичнее способ кодирования, тем меньше разница между этими величинами — см. пример 4, приведенный ниже).
Пример 3. Определить информацию, которую несет в себе 1-й символ в кодировках ASCII и Unicode.
В алфавите ASCII предусмотрено 256 различных символов, т.е. M = 256, а
I = log2 256 = 8 бит = 1 байт
В современной кодировке Unicode заложено гораздо большее количество символов. В ней определено 256 алфавитных страниц по 256 символов в каждой. Предполагая для простоты, что все символы используются, получим, что
I = log2 (256 * 256) = 8 + 8 = 16 бит = 2 байта
Пример 4. Текст, сохраненный в коде ASCII, состоит исключительно из арифметических примеров, которые записаны с помощью 10 цифр от 0 до 9, 4 знаков арифметических операций, знака равенства и некоторого служебного кода, разделяющего примеры между собой. Сравните количество информации, которое несет один символ такого текста, применяя вероятностный и алфавитный подходы.
Легко подсчитать, что всего рассматриваемый в задаче текст состоит из N = 16 различных символов. Следовательно, по формуле Хартли
Iвероятностная = log2 16 = 4 бита
В то же время, согласно вычислениям примера 3, для символа ASCII
Iалфавитная = 8 бит
Двукратный избыток при кодировании символов связан с тем, что далеко не все коды ASCII оказываются в нашем тексте востребованными. В то же время несложно построить вариант специализированной 4-битной кодировки для конкретной задачи4, для которого Iвероятностная и Iалфавитная окажутся равными.
В порядке подведения итогов сравним вероятностный и алфавитный подходы. Первый подход позволяет вычислить предельное (минимально возможное) теоретическое значение количества информации, которое несет сообщение о данном исходе события. Второй — каково количество информации на практике с учетом конкретной выбранной кодировки. Очевидно, что первая величина есть однозначная характеристика рассматриваемого события, тогда как вторая зависит еще и от способа кодирования: в “идеальном” случае обе величины совпадают, однако на практике используемый метод кодирования может иметь ту или иную степень избыточности.
С рассмотренной точки зрения вероятностный подход имеет преимущество. Но, с другой стороны, алфавитный способ заметно проще и с некоторых позиций (например, для подсчета требуемого количества памяти) полезнее.
Бит, будучи минимально возможной порцией информации в компьютере, довольно маленькая единица измерения. Поэтому на практике чаще всего используется другая единица, которая называется 1 байт =
8 бит. С точки зрения устройства компьютера байт замечателен тем, что является минимальной адресуемой информацией в компьютере, иначе говоря, считать из памяти часть байта невозможно. В современных компьютерах все устройства памяти имеют байтовую структуру, а внешние устройства также обмениваются информацией байтами или кратными ему порциями. Как следствие все типы данных (числа, символы и др.) представляются в компьютере величинами, кратными байту.
Примечание. Даже логические переменные, для каждой из которых, казалось бы, достаточно 1 бита, обычно занимают в оперативной памяти полный байт (или иногда ради единообразия даже несколько байт, например, LongBool в Паскале).
С целью получения шкалы для измерения объемов информации в широких пределах от байта с помощью стандартных приставок образуется целая система более крупных производных единиц:
1 килобайт = 1024 байта
1 мегабайт = 1024 килобайта
1 гигабайт = 1024 мегабайта
и т.д. В отличие от общепринятой системы производных единиц (широко используемой, например, в физике) при пересчете применяется множитель 1024, а не 1000. Причина заключается в двоичном характере представления информации в компьютере: 1024 = 210, и, следовательно, лучше подходит к измерению двоичной информации.
Научившись измерять количество информации, можно ставить вопрос, как быстро она передается. Величину, которая равна количеству информации, передаваемому за единицу времени, принято называть скоростью передачи информации. Очевидно, что если за время t по каналу связи передано количество информации I, то скорость передачи вычисляется как отношение I / t.
Скорость передачи данных нельзя сделать сколь угодно большой; ее предельная максимальная величина имеет специальное название — пропускная способность канала связи. Данная характеристика определяется устройством канала и, что не так очевидно, способом передачи сигналов по нему. Иными словами, для разных способов представления данных одна и та же линия связи может иметь разную пропускную способность.
К.Шеннон в созданной им теории информации доказал, что достигнуть при передаче пропускной способности линии можно всегда и путем к этому является повышение эффективности кодирования. Более того, даже при наличии в канале шумов любого уровня всегда можно закодировать сообщение таким образом, чтобы не происходило потери информации.
Обе величины — скорость передачи и пропускная способность — по определению измеряются в одних и тех же единицах, являющихся отношением единиц информации и времени: бит/с, байт/с, Кб/с и т.д.
В информатике используются различные подходы к измерению информации
В информатике используются различные подходы к измерению информации:
Содержательный подход к измерению информации. Сообщение – информативный поток, который в процессе передачи информации поступает к приемнику. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными Информация — знания человека, сообщение должно быть информативно. Если сообщение не информативно, то количество информации с точки зрения человека = 0. (Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику)
Алфавитный подход к измерению информации не связывает кол-во информации с содержанием сообщения. Алфавитный подход — объективный подход к измерению информации. Кол-во информации зависит от объема текста и мощности алфавита. Ограничений на max мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере. Поскольку 256=28, то 1символ несет в тексте 8 бит информации.
Вероятностный подход к измерению информации. Все события происходят с различной вероятностью, но зависимость между вероятностью событий и количеством информации, полученной при совершении того или иного события можно выразить формулой которую в 1948 году предложил Шеннон.
Количество информации — это мера уменьшения неопределенности.
1 БИТ – такое кол-во информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза. БИТ — это наименьшая единица измерения информации
Единицы измерения информации:
1Кб (килобайт) = 210 байт = 1024 байт
1Мб (мегабайт) = 210 Кб = 1024 Кб
1Гб (гигабайт) = 210 Мб = 1024 Мб
I — количество информации
N – количество возможных событий
Pi – вероятности отдельных событий
Задача 1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков
1) всего шаров 50+25+25=100
2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4
3)I= -(1/2 log21/2 + 1/4 log21/4 + 1/4 log21/4) = -(1/2(0-1) +1/4(0-2) +1/4(0-2)) = 1,5 бит
Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно рассчитать по формуле
Задача 2: В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?
т. к. N = 16 шаров, то I = log2 N = log2 16 = 4 бит.
Верно ли, что истрепанная книжка, если в ней нет вырванных страниц, несет для Вас ровно столько же информации, сколько такая же новая?
Каменная скрижаль весом в три тонны несет для археологов столько же информации, сколько ее хороший фотоснимок в археологическом журнале. Не так ли?
Когда московская радиостудия передает последние известия, то одну и ту же информацию получает и подмосковный житель и житель Новосибирска. Но поток энергии радиоволн в Новосибирске намного меньше, чем в Москве.
Следовательно, мощность сигнала, также как и размер и вес носителя, не могут служить оценкой количества информации, переносимой сигналом. Как же оценить это количество?
Из курса физики вы знаете, что прежде, чем измерять значение какой-либо физической величины, надо ввести единицу измерения. У информации тоже есть такая единица — бит, но смысл ее различен при разных подходах к определению понятия “информация”.
Неизмеряемость информации в быту (информация как новизна).
Вы получили какое — то сообщение, например, прочитали статью в любимом журнале. В этом сообщении содержится какое-то количество информации. Как оценить, сколько информации Вы получили? Другими словами, как измерить информацию? Можно ли сказать, что чем больше статья, тем больше информации она содержит?
Разные люди, получившие одно и то же сообщение, по-разному оценивают его информационную ёмкость, то есть количество информации, содержащееся в нем. Это происходит оттого, что знания людей о событиях, явлениях, о которых идет речь в сообщении, до получения сообщения были различными. Поэтому те, кто знал об этом мало, сочтут, что получили много информации, те же, кто знал больше, могут сказать, что информации не получили вовсе. Количество информации в сообщении, таким образом, зависит от того, насколько ново это сообщение для получателя.
В таком случае, количество информации в одном и том же сообщении должно определяться отдельно для каждого получателя, то есть иметь субъективный характер. Но субъективные вещи не поддаются сравнению и анализу, для их измерения трудно выбрать одну общую для всех единицу измерения.
Таким образом, с точки зрения информации как новизны, мы не можем однозначно и объективно оценить количество информации, содержащейся даже в простом сообщении. Что же тогда говорить об измерении количества информации, содержащейся в научном открытии, новом музыкальном стиле, новой теории общественного развития.
Поэтому, когда информация рассматривается как новизна сообщения для получателя, не ставится вопрос об измерении количества информации.
Объемный подход. Измерение информации в технике
(информация как сообщения в форме знаков или сигналов, хранимые, передаваемые и обрабатываемые с помощью технических устройств).
В технике, где информацией считается любая хранящаяся, обрабатываемая или передаваемая последовательность знаков, сигналов, часто используют простой способ определения количества информации, который может быть назван объемным. Он основан на подсчете числа символов в сообщении, то есть связан только с длиной сообщения и не учитывает его содержания.
Длина сообщения зависит от числа знаков, употребляемых для записи сообщения. Например, слово “мир” в русском алфавите записывается тремя знаками, в английском — пятью (peace), а в КОИ -8 — двадцатью четырьмя битами (111011011110100111110010).
В вычислительной технике применяются две стандартные единицы измерения: бит и байт.
Конечно, будет правильно, если Вы скажете: “В слове “Рим” содержится 24 бита информации, а в сообщении “Миру мир!” — 72 бита”. Однако прежде чем измерить информацию в битах, Вы определяете количество символов в этом сообщении. Нам привычней работать с символами. Каждый символ в настоящее время в вычислительной технике кодируется 8-битным или 16-битным кодом. Поэтому, для удобства была введена более “крупная” единица информации в технике (преимущественно в вычислительной) — байт. Теперь Вам легче подсчитать количество информации в техническом сообщении — оно совпадает с количеством символов в нем.
Поскольку компьютер предназначен для обработки больших объемов информации, то используют производные единицы – килобайт (Кб), мегабайт (Мб), гигабайт (Гб).
Обычно приставка “кило” означает тысячу, а приставка “мега” — миллион, но в вычислительной технике все “привязывается” к принятой двоичной системе кодирования.
В 100 Мб можно “уместить”:
50 000 или 150 романов
цветных слайдов высочайшего качества
аудиозапись речи видного политического деятеля
музыкальный фрагмент качества CD — стерео
фильм высокого качества записи
протоколы операций с банковским счетом
Измерение информации в теории информации (информация как снятая неопределенность)
Получение информации (ее увеличение) одновременно означает увеличение знания, что, в свою очередь, означает уменьшение знания или информационной неопределенности.
За единицу количества информации принимают выбор одного из двух равновероятных сообщений (“да” или “нет”, “1” или “0”). Она также названа бит. Вопрос ценности этой информации для получателя — это уже из иной области.
Книга лежит на одной из двух полок — верхней или нижней. Сообщение о том, что книга лежит на верхней полке, уменьшает неопределенность ровно вдвое и несет 1 бит информации.
Сообщение о том, как упала монета после броска — “орлом” или “решкой”, несет один бит информации.
В соревновании участвуют 4 команды. Сообщение о том, что третья команда набрала большее количество очков, уменьшает первоначальную неопределенность ровно в четыре раза (дважды по два) и несет два бита информации.
Очень приближенно можно считать, что количество информации в сообщении о каком-то событии совпадает с количеством вопросов, которые необходимо задать и ответом, на которые могут быть лишь “да” или “нет”, чтобы получить ту же информацию. Причем событие, о котором идет речь, должно иметь равновероятные исходы.
Сколько вопросов надо задать, чтобы отгадать одну из 32 карт (колода без шестерок), если ответами могут быть, лишь “да” или “нет”?
Оказывается достаточно всего лишь 5 вопросов, но задавать их надо так, чтобы после каждого ответа можно было “отбрасывать” из рассмотрения, ровно половину карт, среди которых задуманной не может быть. Такими, например, являются вопросы о цвете масти карты (“Задуманная карта красной масти?”), о типе карты (“Задуманная карта — “картинка”?”) и т. п.
То есть сообщение о том, какая карта из 32 задумана, несет 5 бит информации.
Во всех приведенных примерах число равновероятных исходов события, о котором идет речь в сообщении, было кратным степени числа 2 (4 = 22, 32 = 25). Поэтому сообщение “несло” количество бит информации всегда было целым числом. Но в реальной практике могут встречаться самые разные ситуации.
Сообщение о том, что на светофоре красный сигнал, несет в себе информации больше, чем бит. Попробуйте объяснить почему.
Известно, что Иванов живет на улице Весенней. Сообщение о том, что номер его дома есть число четное, уменьшило неопределенность. Получив такую информацию, мы стали знать больше, но информационная неопределенность осталась, хотя и уменьшилась.
Почему в этом случае мы не можем сказать, что первоначальная неопределенность уменьшилась вдвое (иными словами, что мы получили 1 бит информации)? Если Вы не знаете ответа на этот вопрос, представьте себе улицу, на четной стороне которой, например, четыре дома, а на нечетной — двадцать. Такие улицы не такая уж большая редкость.
Последние примеры показывают, что данное выше определение количества информации слишком упрощено. Уточним его. Но прежде разберем еще один пример.
Пылкий влюбленный, находясь в разлуке с объектом своей любви, посылает телеграмму: “Любишь?”. В ответ приходит не менее лаконичная телеграмма: “Да!”. Сколько информации несет ответная телеграмма? Альтернатив здесь две — либо. Да либо Нет. Их можно обозначить символами двоичного кода 1 и 0. Таким образом, ответную телеграмму можно было бы закодировать всего одним двоичным символом.
Можно ли сказать, что ответная телеграмма несет одну единицу информации?
Если влюбленный уверен в положительном ответе, то ответ “да” почти не даст ему никакой новой информации. То же самое относится и к безнадежно влюбленному, уже привыкшему получать отказы. Ответ “нет” также принесет ему очень мало информации. Но внезапный отказ уверенному влюбленному (неожиданное огорчение) или ответ “да” безнадежному влюбленному (нечаянная радость) несет сравнительно много информации, настолько много, что радикально изменяется все дальнейшее поведение влюбленного, а, может быть, его судьба!
Таким образом, с точки зрения на информацию как на снятую неопределенность количество информации зависит от вероятности получения данного сообщения. Причем, чем больше вероятность события, тем меньше количество информации в сообщении о таком событии.
Иными словами, количество информации в сообщении о каком-то событии зависит от вероятности свершения данного события.
к оценке сообщений был предложен еще в 1928 году Р. Хартли. Расчетная формула имеет вид:
I = log2 N или 2I= N,
где N – количество равновероятных событий (число возможных выборов),
I — количество информации.
Если N = 2 (выбор из двух возможностей), то I = 1 бит.
Бит, выбран в качестве единицы количества информации потому, что принято считать, что двумя двоичными словами исходной длины k или словом длины 2k можно передать в 2 раза больше информации, чем одним исходным словом. Число возможных равновероятных выборов при этом увеличивается в 2k раз, тогда как I удваивается.
Иногда формула Хартли записывается иначе. Так как наступление каждого из N возможных событий имеет одинаковую вероятность p = 1 / N, то N = 1 / p и формула имеет вид
I = log2 (1/p) = — log2 p
В технике (теория кодирования и передачи сообщений) под количеством информации понимают количество кодируемых, передаваемых или хранимых символов.
Бит — двоичный знак двоичного алфавита .
Бит — минимальная единица измерения информации.
Байт — единица количества информации в системе СИ.
Байт — это восьмиразрядный двоичный код, с помощью которого можно представить один символ.
Единицы измерения информации в вычислительной технике
- http://nenuda.ru/%D0%BF%D0%BE%D0%B4%D1%85%D0%BE%D0%B4%D1%8B-%D0%BA-%D0%B8%D0%B7%D0%BC%D0%B5%D1%80%D0%B5%D0%BD%D0%B8%D1%8E-%D0%B8%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%86%D0%B8%D0%B8.html
- http://helpiks.org/8-17694.html
- http://zdamsam.ru/a24111.html
- http://pandia.ru/text/80/258/59225.php