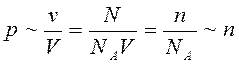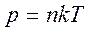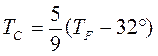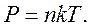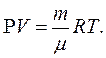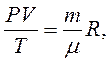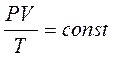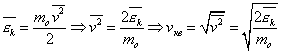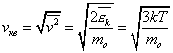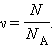Температура является количественной мерой «нагретости» тела. Понятие температуры занимает особое место в ряду физических величин, определяющих состояние системы. Температура не только характеризует состояние теплового равновесия данного тела. Она является также тем параметром, который принимает одинаковое значение для любых двух или большего числа тел, находящихся в тепловом равновесии друг с другом, т.е. характеризует тепловое равновесие системы тел. Это значит, что если два или несколько тел, имеющих разные температуры, привести в контакт, то в результате взаимодействия между молекулами эти тела примут одинаковое значение температуры.
Молекулярно-кинетическая теория позволяет выяснить физический смысл температуры. Сравнивая выражения (2.4) и (2.7), видим, что они совпадают, если положить
(2.8)
(2.9)
Эти соотношения называют вторыми основными уравнениями молекулярно-кинетической теории газов. Они показывают, что абсолютная температура есть величина, определяющая среднюю кинетическую энергию поступательного движения молекул; она является мерой энергии поступательного движения молекул, а тем самым и интенсивности теплового движения молекул. В этом состоит молекулярно-кинетический смысл абсолютной температуры. Как видим, процесс нагревания тела непосредственно связан с увеличением средней кинетической энергии частиц тела. Из (2.9) видно, что абсолютная температура – величина положительная: Значение называется абсолютным нулем температуры. Согласно (2.8) при абсолютном нуле должно полностью прекращаться поступательное движение частиц ( ). Следует, однако, отметить, что при низких температурах газ переходит в конденсированное состояние. Следовательно, теряют смысл и все выводы, сделанные на основе кинетической теории газов. И при абсолютном нуле температуры движение не исчезает. Движение электронов в атомах, движение свободных электронов в металлах полностью сохраняются и при температуре абсолютного нуля. Кроме того, даже при абсолютном нуле сохраняется некоторое колебательное движение атомов внутри молекул и атомов в узлах кристаллической решетки. Существование этих колебаний связано с наличием нулевой энергии у квантового гармонического осциллятора ( ), в качестве которого можно рассматривать указанные выше колебания атомов. Эта энергия не зависит от температуры, а значит, не обращается в нуль и при . При низких температурах классические представления о движении перестают выполняться. В этой области действуют квантовые законы, в соответствии с которыми движение частиц не прекращается, даже если понизить температуру тела до абсолютного нуля. Но скорость этого движения уже не зависит от температуры и это движение не является тепловым. Это подтверждается и принципом неопределенности. Если бы частицы тела покоились, то их положения (координаты x, y, z) и импульсы (проекции импульса px, py, pz) были бы точно определены и т.д., а это противоречит соотношениям неопределенностей и т.д. Абсолютный нуль не достижим. Ниже будет показано, что абсолютный нуль температуры означает такое состояние системы, при котором система находится в состоянии с наименьшей энергией, и поэтому дальнейшее уменьшение интенсивности движения ее частиц за счет отдачи его энергии окружающим телам не возможно.
Формулу (2.7) можно записать в виде.
Эта формула может служить определением понятия абсолютной температуры для одноатомного газа. Температуру любой другой системы можно определить как величину, равную температуре одноатомного газа, находящегося в тепловом равновесии с этой системой. Определение температуры с помощью этой формулы верно вплоть до температур, при которых уже нельзя пренебречь вероятностью возникновения электронно-возбужденных состояний атомов газа.
Соотношение (2.8) позволяет ввести так называемую среднюю квадратичную скорость молекулы , определив ее как
Понятие абсолютной температуры можно более строго ввести в статистической физике, где ее можно рассматривать как модуль статистического распределения частиц по энергиям. Отметим также, что поскольку температура, так же как и давление, как видно из формул (2.7) и (2.8), определяется средней кинетической энергией молекулы идеального газа, то тони представляют собой статистические величины и, следовательно, бессмысленно говорить о температуре или давлении одной или небольшого числа молекул.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 8558 — 

Как было установлено выше изменение давления Δp пропорционально изменению 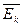
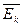
Опытным путем установлено, что давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p
T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда
где N – число молекул в сосуде, NA – постоянная Авогадро, n = N / V – концентрация молекул (т. е. число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:
где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Л. Больцмана (1844–1906 гг.), одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант.
Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
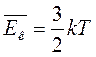
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.
Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул.
Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными.
Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.
Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).
Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (TF), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,
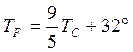
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура TС = 20 °С по шкале Кельвина равна TК = 293,15 К.
Уравнение состояния идеального газа или уравнение Менделеева — Клапейрона является обобщением законов идеального газа, открытых экспериментально до создания МКТ. Однако, из основного уравнения МКТ, можно получить уравнение состояния идеального газа. Для этого используем уравнение в виде
Так как 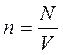
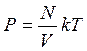
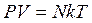
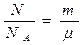
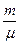
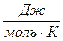
Уравнение состояния газа часто удобно использовать в записи, предложенной Клапейроном, если количество вещества не изменяется, то
или
Последнее уравнение часто называют обобщённым газовым законом. Тот факт, что из основного уравнения молекулярно-кинетической теории идеального газа можно вывести уравнение состояния идеального газа, подтверждает верность молекулярно-кинетической теории вещества.
Дата добавления: 2017-01-08 ; просмотров: 3883 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Число степеней свободы.
Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.
На рис. 1.1 показаны одноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3).
Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.
Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 — поступательного и 3 — вращательного движения (i = 6).
В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная 1/2(kT). Таким образом, средняя энергия одной молекулы равна

1.2. Температура и ее измерение.
Температура с молекулярно-кинетической точки зрения — физическая величина, характеризующая интенсивность хаотического, теплового движения всей совокупности частиц системы и пропорциональная средней кинетической энергии поступательного движения одной частицы. Связь между кинетической энергией, массой и скоростью выражается следующей формулой:

Таким образом, частицы одинаковой массы и значения скорости имеют одну и ту же температуру. C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия 

Так как энергия равномерно распределяется по степеням свободы, то связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой для идеального газа дается формулой

где k — постоянная Больцмана, 
Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы. Формула (4.7) позволяет выяснить смысл абсолютного нуля: 

Давление может быть выражено через среднюю кинетическую энергию поступательного движения молекулы. Если воспользоваться формулами (1.1.) и (1.3), то получим

Уравнение (4.8) называется основным уравнением молекулярно-кинетической теории. Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, заключенных в единице объема.
Для измерения температуры выбирается некоторый термодинамический параметр термометрического вещества. Изменение этого параметра однозначно связывается с изменением температуры. Большинство термометров измеряют собственную температуру. Средства измерения температуры обычно проградуированы по относительным шкалам — Цельсия или Фаренгейта.
На практике для измерения температуры используют
- жидкостные и механические термометры,
- термопару,
- термосопротивление
- термометр сопротивления
- тазовый термометр
- тирометр
Жидкостные термометры основаны на принципе изменения объёма жидкости, которая залита в термометр (обычно это спирт или ртуть), при изменении температуры окружающей среды. В связи с запретом применения ртути во многих областях деятельности ведется поиск альтернативных наполнений для бытовых термометров. Например, такой заменой может стать сплав галинстан.
Механические термометры действуют по тому же принципу, что и жидкостные, но в качестве датчика обычно используется металлическая спираль или лента из биметалла.
Термометры на термопарах основаны контактной разности потенциалов – контакт между металлами с разной электроотрицательностью создаёт контактную разность потенциалов, зависящую от температуры.
Термометры сопротивления являются наиболее точными и стабильными во времени. В основе их работы лежит зависимость электрического сопротивления от температуры платиновой проволоки или платинового напыления на керамику. Температурный диапазон −200 — + 850 C.
Газовый термометр – прибор для измерения температуры, основанный на законе Шарля, который установил прямую пропорциональную зависимость между давлением газа и температурой при постоянном объеме. Наиболее точные результаты получаются, если в качестве рабочего тела использовать водород или гелий.
Пирометр – прибор для бесконтактного измерения температуры тел. Принцип действия основан на измерении мощности теплового излучения объекта измерения преимущественно в диапазонах инфракрасного излучения и видимого света. Например, позволяют визуально определять температуру нагретого тела путем сравнения его цвета с цветом эталонной нити.
1.3. Шкалы температур
Из того, что температура — это кинетическая энергия молекул, ясно, что наиболее естественно измерять её в энергетических единицах (т.е. в системе СИ в джоулях). Однако измерение температуры началось задолго до создания молекулярно-кинетической теории, поэтому практические шкалы измеряют температуру в условных единицах – градусах.
Шкала Кельвина.Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры – кельвин (К). Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры – абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию. Абсолютный ноль определён как 0 K, что равно −273.15 °C (точно). Шкала температур Кельвина, в которой начало отсчёта ведётся от абсолютного нуля.
Шкала Цельсия. В технике, медицине, метеорологии и в быту используется шкала Цельсия. В этой шкале за 0 принимают точку замерзания воды, а за 100° – точку кипения воды при нормальном атмосферном давлении. Поскольку температура замерзания и кипения воды недостаточно хорошо определена, в настоящее время шкалу Цельсия определяют через шкалу Кельвина: градус Цельсия равен кельвину, абсолютный ноль принимается за −273,15° C. Шкала Цельсия практически очень удобна, поскольку вода очень распространена на нашей планете и на ней основана наша жизнь. Ноль Цельсия – особая точка для метеорологии, поскольку связана с замерзанием атмосферной воды. Шкала предложена Андерсом Цельсием в 1742 г.
Шкала Фаренгейта. В Англии и, в особенности, в США используется шкала Фаренгейта. Ноль градусов Цельсия – это 32 градуса Фаренгейта, а градус Фаренгейта равен 5/9 градуса Цельсия. В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t°С) соотношением t°С = 5/9 (t°F — 32), 1 F = 9/5°С + 32. Предложена Г. Фаренгейтом в 1724.
Шкала Реомюра предложена в 1730 году Р.А. Реомюром, который описал изобретённый им спиртовой термометр. Во многих информационных изданиях утверждается, что шкала термометра Реомюра определялась двумя опорными точками замерзания и кипения воды. На самом деле опорная точка в первом термометре Реомюра была одна. Не стоит забывать, что первый термометр Реомюра был заполнен спиртом, температура кипения которого составляет 80 градусов по Цельсию (≈78 градусов Цельсия), что ниже температуры кипения воды. Естественно, измерить своим термометром температуру в 100 градусов по Цельсию он не мог, спирт бы кипел. Вместо этого Реомюр кратковременно опускал колбу термометра в кипящую воду и в тот момент, когда спирт закипал, отмечал его уровень на стеклянной трубке. Затем он вытаскивал термометр, ждал, пока кипение прекратится, и повторял эксперимент снова. Так образом им был найден максимальный уровень, при котором спирт начинал кипеть. Спирт при этом расширился на 8 % от своего первоначального объёма и его уровень в стеклянной трубке составил 1080 условных единиц, что соответствовало 80 градусам Реомюра. Однако, из-за того, что в качестве жидкости в те времена использовались не только спирт, но и различные его водные растворы, то многими изготовителями и пользователями термометров ошибочно считалось, что 80 градусов Реомюра это температура кипения воды. Из равенства 100 градусов Цельсия = 80 градусов Реомюра получается 1 C = 0,8°R (соответственно 1°R = 1,25 C). Хотя на самом деле на оригинальной шкале Реомюра должно быть 1°R = 0,925 C. Ещё при жизни Реомюра были проведены измерения точки кипения воды в градусах его шкалы (но не со спиртовым термометром – это было невозможно). Для точки кипения воды в градусах Реомюра получается значение 108.
Единица – градус Реомюра (°R), 1°R равен 1/80 части температурного интервала между опорными точками – температурой таяния льда (0°R) и кипения воды (80°R) 1°R = 1,25°C. В настоящее время шкала вышла из употребления, дольше всего она сохранялась во Франции, на родине автора.
1.4. Уравнение состояния идеального газа
Самой простой системой частиц является газ. В то же время его изучение имеет большое практическое значение, хотя бы потому, что газообмен определяет состояние всей биосферы Земли, в том числе человека. Вместо реального газа, между молекулами которого действуют сложные силы взаимодействия, мы будем рассматривать физическую модель — идеальный газ.
Идеальным газом называется газ, в котором собственными размерами молекул и взаимодействием между молекулами можно пренебречь. Реальные разреженные газы ведут себя подобно идеальному, так как лишь небольшая доля молекул в них находится в состоянии соударения. Например, такие газы, как воздух, кислород, азот и т. д. при комнатной температуре и атмосферном давлении по своим свойствам близки к идеальному.
Состояние заданной массы газа определяется значениями трех термодинамических параметров: давления p, объема V и температуры T. Связь между параметрами называется уравнением состояния. Уравнение состояния идеального газа может быть записано в разных формах.
В наиболее общем виде уравнение состояния идеального газа установил эмпирически французский ученый Б.П. Клапейрон и русский ученый Д.И. Менделеев. Для двух различных состояний уравнение Клапейрона имеет вид

Уравнение Клапейрона-Менделеева имеет вид:


где p — давление; V — объем; T — термодинамическая или абсолютная температура (вычисляется по шкале Кельвина, которая связана с температурой по шкале Цельсия соотношением 

Уравнение Клапейрона — Менделеева формулируется так: произведение давления идеального газа на его объем, деленное на термодинамическую температуру, есть величина постоянная для данной массы газа.
Отношение массы вещества к молярной массе называется количеством вещества

и измеряется в молях.
Уравнению (1.6) можно придать другой вид. Обозначим через m — массу одной молекулы, а N — полное число молекул. Тогда
Количество вещества равно

Подставим (1.8) в (1.6) и получим
Отношение газовой постоянной к числу Авогадро есть постоянная Больцмана
Тогда другая форма записи уравнения состояния идеального газа имеет вид

Найдем связь давления и концентрации газа.
Концентрацией называется число молекул, заключенных в единице объема:

Из этого следует, что давление пропорционально концентрации, т. е.

Это еще одна форма записи уравнения состояния идеального газа.
1.5. Изопроцессы. Законы Бойля-Мариотта, Гей-Люссака, Шарля.
Состояние идеального газа определяется тремя параметрами: p — давление, V — объем и T — термодинамическая температура. Изменение хотя бы одного параметра приводит к новому состоянию. Переход системы из одного состояния в другое называется процессом. Изопроцессом называется процесс, при котором один из параметров остается постоянным. Существует три изопроцесса, законы которых легко получить из уравнения (1.5).
1. Изотермический (при постоянной температуре). Это процесс описывается законом Бойля и Мариотта. Для данной массы газа при постоянной температуре произведение давление на объем газа есть величина постоянная (рис. 1.2, а).

2. Изобарный (изобарический) – при постоянном давлении. Подчиняется закону Гей-Люссака. Для данной массы газа при постоянном давлении объем газа прямо пропорционален абсолютной температуре (рис. 1.2., б).

3. Изохорный (изохорический) – при постоянном объеме. Подчиняется закону Шарля. Для данной массы газа при постоянном объеме давление газа прямо пропорционално абсолютной температуре (рис. 1.2., в).

Рис. 1.2. а, б, в – изотермы, изобары и изохоры идеального газа, соответственно
Эти частные законы позволяют связать конечные параметры с начальными характеристиками.
42. Давление и температура с точки зрения молекулярно кинетической теории.
Любое макроскопическое тело или группа макроскопических тел называется термодинамической системой.
Тепловое или термодинамическое равновесие — такое состояние термодинамической системы, при котором все ее макроскопические параметры остаются неизменными: не меняются объем, давление, не происходит теплообмен, отсутствуют переходы из одного агрегатного состояния в другое и т.д. При неизменных внешних условиях любая термодинамическая система самопроизвольно переходит в состояние теплового равновесия.
Температура — физическая величина, характеризующая состояние теплового равновесия системы тел: все тела системы, находящиеся друг с другом в тепловом равновесии, имеют одну и ту же температуру.
Абсолютный нуль температуры — предельная температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю или должен быть равен нулю объем идеального газа при постоянном давлении.
Давление — это явление когда частицы (молекулы) «давят» на сосуд (под действием внутренней энергии и теплового беспорядочного движения ударяются в стенки сосуда). Чем больше кинетическая энергия частицы тем больше сила удара об стенку приходящаяся на единицу площади, тем больше давление.
43.Среднеквадратичная скорость молекул газа.
Среднеквадратичная скорость молекул равна квадратному корню из среднего квадрата скорости молекул: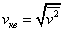
Вычислим среднеквадратичную скорость из средней кинетической энергии молекул, которую мы легко можем сосчитать:
Оказывается у молекул есть средняя скорость (по модулю), которая зависит от температуры, и основная часть молекул имеет модуль скорости близкий к ней. Эту скорость мы не можем вычислить, но можем легко посчитать среднеквадратичную скорость движения молекул газа, которая отличается от средней скорости коэффициентом порядка 1.
44.Уравнение изобарного процесса. Его график в координатах pv, pt, vt.
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа.Согласно закону Гей-Люссака, при изобарном процессе в идеальном газе 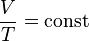
Работа, совершаемая газом при расширении или сжатии газа, равна 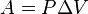
Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: 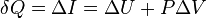
Справочник
Молекулярно-кинетическое определение Температура с молекулярно-кинетической точки зрения — физическая величина, характеризующая интенсивность хаотического, теплового движения всей совокупности частиц системы и пропорциональная средней кинетической энергии поступательного движения одной частицы. Связь между кинетической энергией, массой и скоростью выражается следующей формулой: Ek = 1 /2m • v 2 Таким образом частицы одинаковой массы и имеющие одинаковую скорость имеют и одинаковую температуру. Средняя кинетическая энергия частицы связана с термодинамической температурой постоянной Больцмана: Eср = i/2kT где: i — число степеней свободы k = 1.380 6505(24) × 10 -23 Дж/K — постоянная Больцмана T — температура; Термодинамическое определение Температура — величина, обратная изменению энтропии (степени беспорядка) системы при добавлении в систему единичного количества теплоты: 1/T = ΔS/ΔQ. История термодинамического подхода: Слово «температура» возникло в те времена, когда люди считали, что в более нагретых телах содержится большее количество особого вещества — теплорода, чем в менее нагретых. Поэтому температура воспринималась как крепость смеси вещества тела и теплорода. По этой причине единицы измерения крепости спиртных напитков и температуры называются одинаково — градусами. В равновесном состоянии температура имеет одинаковое значение для всех макроскопических частей системы. Если в системе два тела имеют одинаковую температуру, то между ними не происходит передачи кинетической энергии частиц (тепла). Если же существует разница температур, то тепло переходит от тела с более высокой температурой к телу с более низкой, потому что суммарная энтропия при этом возрастает. Температура связана также с субъективными ощущениями «тепла» и «холода», связанными с тем, отдает ли живая ткань тепло или получает его. Некоторые квантовомеханические системы могут находится в состоянии, при котором энтропия не возрастает, а убывает при добавлении энергии, что формально соответствует отрицательной абсолютной температуре. Однако такие состояния находятся не «ниже абсолютного нуля», а «выше бесконечности», поскольку при контакте такой системы с телом, обладающим положительной температурой, энергия передается от системы к телу, а не наоборот (подробнее см. Квантовая термодинамика). Свойства температуры изучает раздел физики — термодинамика. Температура также играет важную роль во многих областях науки, включая другие разделы физики, а также химию и биологию.
Физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Т. одинакова для всех частей изолированной системы, находящейся в равновесии термодинамическом.
Двойкам нет
Молекулярная физика — это один из разделов физики, который изучает физические свойства тел в различных агрегатных состояниях, а также их молекулярное строение, силы взаимодействия между частицами, из которых состоят тела, и характер теплового движения этих частиц.
Молекулярно-кинетическая теория (МКТ) — это раздел молекулярной физики, где объясняется строение и свойства тел за счет движения и взаимодействия частиц, из которых состоят эти тела.
Три положения молекулярно-кинетической теории:
- все тела состоят из частиц, таких как атомы, молекулы, ионы;
- частицы из которых состоят тела, имеют хаотическое (беспорядочное) движение;
- взаимодействие тел друг с другом происходит силами притяжения и отталкивания.
Молекула — это самая наименьшая частица вещества, которая имеет все его химические свойства.
Атом — это самая наименьшая частица химического элемента. Молекула состоит из равного количества положительно и отрицательно заряженных частиц, поэтому она электрически нейтральна.
Молекула состоит из атомов, которые соединены химическими связями.
Макромолекула — это такая молекула, которая имеет тысячи повторяющихся групп атомов.
Относительная атомная или молекулярная масса — это величина, которая равна отношению массы молекулы (атома) к 1/12 массы атома изотопа углерода:
Количество вещества — это такая величина, которая характеризует число структурных элементов, из которых состоит система.
Структурные элементы — это атомы, молекулы, ионы и другие частицы.
Количество вещества определяется формулой:
Число Авогадро (постоянная Авогадро) — это число структурных элементов, содержащихся в одном моле вещества:
В Международной системе единиц единицей количества вещества является моль.
Молярная масса — это величина, которая равна отношению массы однородного вещества к количеству вещества:
В Международной системе единиц единицей молярной массы является килограмм на моль (кг/моль).
Изотермический процесс — это такой процесс, при котором происходит изменение состояния термодинамической системы, если температура не меняется.
Изотерма — это линия на диаграмме состояния, которая является гиперболой, показывает процесс изменения состояния термодинамической системы.
Изобарный процесс — это процесс, при котором происходит изменение состояния термодинамической системы, если давление не меняется.
Изобара — это линия на диаграмме состояния, которая показывает изменения состояния термодинамической системы при изобарном процессе.
Изохорный процесс — это процесс, при котором происходит изменение состояния термодинамической системы, если объем не меняется.
Изохора — это линия на диаграмме состояния, которая показывает изменения состояния термодинамической системы при изохорном процессе.
Смесь идеальных газов — совокупность нескольких разнохарактерных газов, которые при рассматриваемых условиях не вступают друг с другом в химические реакции.
Парциальное давление — это такое давление газа, которое является одним из составляющих газовой смеси, которое он бы оказывал, если бы при той же температуре один занимал объем, равный объему смеси.
Что такое температура с точки зрения мкт
Молекулярная физика и термодинамика – это по существу две разные по своим подходам, но тесно связанные науки, занимающиеся одним и тем же – изучением макроскопических свойств физических систем, но совершенно разными методами.
В основе молекулярной физики или молекулярно-кинетической теории лежат определенные представления о строении вещества. Для установления законов поведения макроскопических систем, состоящих из огромного числа частиц, в молекулярной физике используются различные модели вещества, например, модели идеального газа.
Молекулярная физика является статистической теорией, т. е. теорией, которая рассматривает поведение систем, состоящих из огромного числа частиц (атомов, молекул), на основе вероятностных моделей. Она стремится на основе статистического подхода установить связь между экспериментально измеренными макроскопическими величинами (давление, объем, температура и т.д.) и микроскопическими характеристиками частиц, входящих в состав системы (масса, импульс, энергия и т.д.).
В отличие от молекулярно-кинетической теории, термодинамика при изучении свойств макроскопических систем не опирается ни на какие представления о молекулярной структуре вещества. Термодинамика является наукой феноменологической . Она делает выводы о свойствах вещества на основе законов, установленных на опыте, таких, как закон сохранения энергии. Термодинамика оперирует только с макроскопическими величинами (давление, температура, объем и т.п.), которые вводятся на основе физического эксперимента.
Оба подхода – термодинамический и статистический – не противоречат, а дополняют друг друга. Только совместное использование термодинамики и молекулярно-кинетической теории может дать наиболее полное представление о свойствах систем, состоящих из большого числа частиц.
Молекулярно-кинетическая теория
3.1. Основные положения МКТ
Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.
В основе молекулярно-кинетической теории лежат три основных положения:
Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
Атомы и молекулы находятся в непрерывном хаотическом движении.
Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
 | |||||||
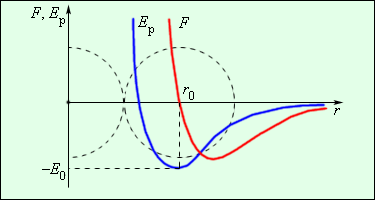
| Рисунок 3.1.1. Наиболее ярким экспериментальным подтверждением представлений молекулярно-кинетической теории о беспорядочном движении атомов и молекул является броуновское движение . Это тепловое движение мельчайших микроскопических частиц, взвешенных в жидкости или газе. Оно было открыто английским ботаником Р. Броуном в 1827 г. Броуновские частицы движутся под влиянием беспорядочных ударов молекул. Из-за хаотического теплового движения молекул эти удары никогда не уравновешивают друг друга. В результате скорость броуновской частицы беспорядочно меняется по модулю и направлению, а ее траектория представляет собой сложную зигзагообразную кривую (рис. 3.1.1). Теория броуновского движения была создана А. Эйнштейном в 1905 г. Экспериментально теория Эйнштейна была подтверждена в опытах французского физика Ж. Перрена, проведенных в 1908–1911 гг. Главный вывод теории А. Эйнштейна состоит в том, что квадрат смещения броуновской частицы от начального положения, усредненный по многим броуновским частицам, пропорционален времени наблюдения . Это соотношение выражает так называемый диффузионный закон . Как следует из теории коэффициент пропорциональности монотонно возрастает с увеличением температуры. Постоянное хаотичное движение молекул вещества проявляется также в другом легко наблюдаемом явлении – диффузии . Диффузией называется явление проникновения двух или нескольких соприкасающихся веществ друг в друга. Наиболее быстро процесс протекает в газе, если он неоднороден по составу. Диффузия приводит к образованию однородной смеси независимо от плотности компонентов. Так, если в двух частях сосуда, разделенных перегородкой, находятся кислород O2 и водород H2, то после удаления перегородки начинается процесс взаимопроникновения газов друг в друга, приводящий к образованию взрывоопасной смеси – гремучего газа. Этот процесс идет и в том случае, когда легкий газ (водород) находится в верхней половине сосуда, а более тяжелый (вислород) – в нижней. Значительно медленнее протекают подобные процессы в жидкостях. Взаимопроникновение двух разнородных жидкостей друг в друга, растворение твердых веществ в жидкостях (например, сахара в воде) и образование однородных растворов – примеры диффузионных процессов в жидкостях. В реальных условиях диффузия в жидкостях и газах маскируется более быстрыми процессами перемешивания, например, из-за возникновения конвекционных потоков. Наиболее медленно процесс диффузии протекает в твердых телах. Однако, опыты показывают, что при контакте хорошо очищенных поверхностей двух металлов через длительное время в каждом из них обнаруживается атомы другого металла. Диффузия и броуновское движение – родственные явления. Взаимопроникновение соприкасающихся веществ друг в друга и беспорядочное движение мельчайших частиц, взвешенных в жидкости или газе, происходят вследствие хаотичного теплового движения молекул. Силы, действующие между двумя молекулами, зависят от расстояния между ними. Молекулы представляют собой сложные пространственные структуры, содержащие как положительные, так и отрицательные заряды. Если расстояние между молекулами достаточно велико, то преобладают силы межмолекулярного притяжения. На малых расстояниях преобладают силы отталкивания. Зависимости результирующей силы и потенциальной энергии взаимодействия между молекулами от расстояния между их центрами качественно изображены на рис. 3.1.2. При некотором расстоянии сила взаимодействия обращается в нуль. Это расстояние условно можно принять за диаметр молекулы. Потенциальная энергия взаимодействия при минимальна. Чтобы удалить друг от друга две молекулы, находящиеся на расстоянии , нужно сообщить им дополнительную энергию . Величина называется глубиной потенциальной ямы или энергией связи .
|
- http://poznayka.org/s80053t1.html
- http://helpiks.org/3-77725.html
- http://studfiles.net/preview/436427/page:3/
- http://temperatures.ru/slovar/slovar_one/103
- http://xn----7sbfhivhrke5c.xn--p1ai/%D0%BC%D0%BE%D0%BB%D0%B5%D0%BA%D1%83%D0%BB%D1%8F%D1%80%D0%BD%D0%BE-%D0%BA%D0%B8%D0%BD%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F-%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F/
- http://physics.ru/courses/op25part1/content/chapter3/section/paragraph1/theory.html