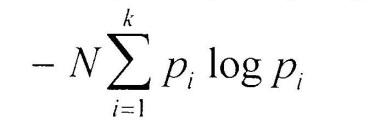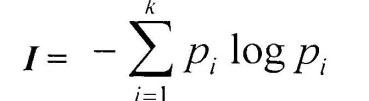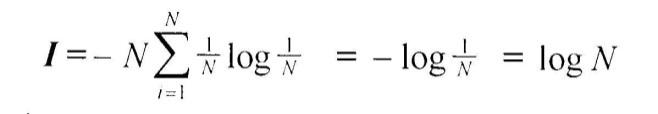Что означает термин энтропия точки зрения теории информации

K
Это незавершённая статья из области эвентологии и её применений, редактируемая при участии Мастера

Энтропи́я в теории информации — мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.

Так, возьмём, например, последовательность символов, составляющих какое-либо предложение на русском языке. Каждый символ появляется с разной частотой, следовательно, неопределённость появления для некоторых символов больше, чем для других. Если же учесть, что некоторые сочетания символов встречаются очень редко, то неопределённость ещё более уменьшается (в этом случае говорят об энтропии n-ого порядка, см. Условная энтропия).

Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу. Ср. тж. Термодинамическая энтропия

Формальные определения [ править ]

Энтропия независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:

Эта величина также называется средней энтропией сообщения. Величина называется частной энтропией, характеризующей только i-e состояние.

Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

Шеннон вывел это определение энтропии из следующих предположений:

• мера должна быть непрерывной; т. е. изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение энтропии;
• в случае, когда все варианты (буквы в приведенном примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать полную энтропию;
• должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых энтропия конечного результата должна будет являтся суммой энтропий промежуточных результатов.

Шеннон показал, что любое определение энтропии, удовлетворяющее этим предположениям, должно быть в форме:

где K — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии (H = − p₁ log₂p₁ − … − p_n log₂p_n), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надежной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидания «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т.д. См. Цепи Маркова.

В общем случае b-арная энтропия (где b равно 2,3. ) источника = (S,P) с исходным алфавитом S = a₁, …, a_n> и дискретным распределением вероятности P = p₁, …, p_n> где p_i является вероятностью a_i (p_i = p(a_i)) определяется формулой:

Определение энтропии Шеннона очень связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между понятиями энтропии в термодинамике и теории информации. Например, демон Максвелла также противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.

Условная энтропия [ править ]

Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а следовательно и энтропия) очевидно меньше. Для учёта таких фактов используется условная энтропия.

Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (т.е. вероятности двухбуквенных сочетаний):

где — это состояние, зависящее от предшествующего символа, и — это вероятность , при условии, что был предыдущим символом.

Так, для русского алфавита без буквы «ё» .

Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются т.н. канальные матрицы. Так, для описания потерь со стороны источника (т.е. известен посланный сигнал), рассматривают условную вероятность получения приёмником символа при условии, что был отправлен символ . При этом канальная матрица имеет следующий вид:

Очевидно, вероятности, расположенные по диагонали описывают вероятность правильного приёма, а сумма всех элементов столбца даст вероятность появления соответствующего символа на стороне приёмника — . Потери, приходящиеся на предаваемый сигнал , описываются через частную условную энтропию:

Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:

означает энтропию со стороны источника, аналогично рассматривается — энтропия со стороны приёмника: вместо всюду указывается (суммируя элементы строки можно получить , а элементы диагонали означают вероятность того, что был отправлен именно тот символ, который получен, т.е. вероятность правильной передачи).

Взаимная энтропия [ править ]

Взаимная энтропия, или энтропия объединения, предназначена для рассчёта энтропии взаимосвязанных систем (энтропии совместного появления статистически зависимых сообщений) и обозначается , где , как всегда, характеризует передатчик, а — приёмник.

Взаимосязь переданных и полученных сигналов описывается вероятностями совместных событий , и для полного описания характеристик канала требуется только одна матрица:

Для более общего случая, когда описывается не канал, а просто взаимодействующие системы, матрица необязательно должна быть квадратной. Очевидно, сумма всех элементов столбца с номером даст , сумма строки с номером есть , а сумма всех элементов матрицы равна 1. Совместная вероятность событий и вычисляется как произведение исходной и условной вероятности,

Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:

Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:

Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем

Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.

Свойства [ править ]

Важно помнить, что энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию бита на одно кидание (при условии его независимости). У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю: . Так, к примеру, опытным путём можно установить, что энтропия английского текста равна 1,5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании.

1. Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.
2. Количество энтропии не всегда выражается целым числом бит.

Альтернативное определение [ править ]

Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет пунктам 1)—3):

1) H(p₁, …, p_n) определена и непрерывна для всех p₁, …, p_n, где p_i [0,1] для всех i = 1, …, n и p₁ + … + p_n = 1. (Заметьте, что эта функция зависит только от распределения вероятностей, а не от алфавита.)

2) Для целых положительных n, должно выполняться следующее неравенство:

3) Для целых положительных b_i, где b₁ + … + b_n = n, должно выполняться равенство:

Эффективность [ править ]

Исходный алфавит, встречающийся на практике, имеет вероятностное распределение, которое далеко от оптимального. Если исходный алфавит имел n символов, тогда он может может быть сравнён с «оптимизированным алфавитом», вероятностное распределение которого однородно. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах.

Из этого следует, что эффективность исходного алфавита с n символами может быть определена просто как равная его n-арной энтропии.

Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, на практике, — кодирования Хаффмана, кодирования Лемпеля-Зива или арифметического кодирования.

История [ править ]

В 1948 году, исследуя проблему рациональной передачи информации через зашумленный коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки двух основных направлений: теории информации, которая использует понятие вероятности и эргодическую теорию для изучения статистических характеристик данных и коммуникационных систем, и теории кодирования, в которой используются главным образом алгебраические и геометрические инструменты для разработки эффективных шифров.

Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.

2. Количество информации, ее определение. Единица информации. Понятие энтропии в теории информации.

КОЛИЧЕСТВО ИНФОРМАЦИИ, ЕЕ ОПРЕДЕЛЕНИЕ. ЕДИНИЦА ИНФОРМАЦИИ.

Количество информации – в теории информации – мера информации, сообщаемой появлением события определённой вероятности; или мера оценки информации, содержащейся в сообщении или мера , характеризующая уменьшение неопределённости, содержащейся в одной случайной величине относительно другой.

Предположим, что какое-то событие имеет m равновероятных исходов. Таким событием может быть, например, появление любого символа из алфавита, содержащего m таких символов. Как изме­рить количество информации, которое может быть передано при помощи такого алфавита? Это мож­но сделать, определив число N возможных сообщений, которые могут быть переданы при помощи этого алфавита. Если сообщение формируется из одного символа, то N = m, если из двух, то N = m*m = m 2 . Если сообщение содержит n символов (n— длина сообщения), то N = m n Казалось бы, ис­комая мера количества информации найдена. Ее можно понимать как меру неопределенности опыта, если под опытом подразумевать случайный выбор какого-либо сообщения из некоторого числа воз­можных. Однако эта мера не совсем удобна. При наличии алфавита, состоящего из одного символа, т.е. когда m = 1, возможно появление только этого символа. Следовательно, неопределенности в этом случае не существует, и появление этого символа не несет никакой информации. Между тем, значение N при m = 1 не обращается в нуль. Для двух независимых источников сообщений (или ал­фавита) с N₁ и N₂ числом возможных сообщений общее число возможных сообщений N = N₁N₂, в то время как логичнее было бы считать, что количество информации, получаемое от двух независимых источников, должно быть не произведением, а суммой составляющих величин. Выход из положения был найден Р.Хартли, который предложил информацию I, приходящуюся на одно сообщение, определять логарифмом общего числа возможных сообщений N: I(N)=logN (1)

Если-же все множество возможных сообщений состоит из одного (N = m = 1), то I(N) = log 1 = , что соответствует отсутствию информации в этом случае. При наличии независимых источников информации с N1 и N2 числом возможных сообщений

I(N) = logN = log N₁N₂= log N₁+ logN₂, т.е. количество информации, приходящееся на одно сообщение, равно сумме количеств информации, которые были бы получены от двух независимых источников, взятых порознь. Формула, предложен­ная Хартли, удовлетворяет предложенным требованиям. Поэтому ее можно использовать для изме­рения количества информации.

Если возможность появления любого символа алфавита равновероятна (а мы до сих пор пред­полагали, что это именно так), то эта вероятность р = 1/m. Полагая, что N=m,

I = logN = logm = logl/p = -log p, (2) т.е. количество информации на каждый равновероятный сигнал равно минус логарифму вероятности отдельного сигнала.

Полученная формула позволяет для некоторых случаев определить количество информации. Однако для практических целей необходимо задаться единицей его из­мерения. Для этого предположим, что информация — это устраненная неопределен­ность. Тогда в простейшем случае неопределенности выбор будет производиться между двумя взаимоисключающими друг друга равновероятными сообщениями, на­пример между двумя качественными признаками: положительным и отрицатель­ным импульсами, импульсом и паузой и т.п. Количество информации, переданное в этом простейшем случае, наиболее удобно принять за единицу количества информа­ции. Именно такое количество информации может быть получено, если применить формулу (2) и взять логарифм по основанию 2. Тогда I = -log₂p = —logl/2 = log₂2 = 1

Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита. На­звание bit образовано из двух начальных и последней букв английского выражения binary digit, что значит двоичная единица. Бит является не только единицей количества информации, но и единицей измерения степени неопределенности. При этом имеется в виду неопределенность, которая содержится в одном опыте, имеющем два равноверо­ятных исхода.

На количество информации, получаемой из сообщения, влияет фактор неожиданности его для получения того или иного сообщения. Чем меньше эта вероятность, тем сообщение более неожидан­но и, следовательно, более информативно. Сообщение, вероятность которого высока и, соответст­венно, низка степень неожиданности, несет немного информации.

Р. Хартли понимал, что сообщения имеют различную вероятность и, следова­тельно, неожиданность их появления для получателя неодинакова. Но, определяя ко­личество информации, он пытался полностью исключить фактор «неожиданности». Поэтому формула Хартли позволяет определить количество информации в сообщении только для случая, когда появление символов равновероятно и они статистически не­зависимы. На практике эти условия выполняются редко. При определении количества информации необходимо учитывать не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность их получения.

Наиболее широкое распространение при определении среднего количества ин­формации, которое содержится в сообщениях от источников самой разной природы, получил подход К. Шеннона. Рассмотрим следующую ситуацию.

Источник передает элементарные сигналы k различных типов. Проследим за достаточно длин­ным отрезком сообщения. Пусть в нем имеется N₁ сигналов первого типа, N₂ сигналов второго типа, …, N_k сигналов k-го типа, причем N₁+ N₂+ . + N_k= N — общее число сигналов в наблюдаемом от­резке, f₁, f₂. f_k— частоты соответствующих сигналов.

При возрастании длины отрезка сообщения каждая из частот стремится к фиксированному пре­делу, т.е.

lim f_i= p_i(i = 1,2. k), где p_i можно считать вероятностью сигнала. Предположим, получен сигнал i-того типа с вероятностью p_i, содержащий -logp_i единиц информации. В рассматриваемом отрезке i-й сигнал встретится примерно Np_i раз (будем считать, что N достаточно велико), и общая информация, доставленная сигналами этого типа, будет равна произведению -Np_ilogp_i. То же отно­сится к сигналам любого другого типа, поэтому полное количество информации, доставленное от­резком из N сигналов, будет примерно равно

Чтобы определить среднее количество информации, приходящееся на один сигнал, т.е. удель­ную информативность источника, нужно это число разделить на N. При неограниченном росте числа сигналов приблизительное равенство перейдет в точное. В результате будет получено асим­птотическое соотношение — формула Шеннона:

В последнее время она стала не менее распространенной, чем знаменитая формула Эйнштейна Е=mс 2 . Оказалось, что формула, предложенная Хартли, представляет собой частный случай более общей формулы Шеннона. Если в формуле Шеннона принять, что p₁= p₂= . = p_i= . p_n= 1/N,

то

Знак минус в формуле Шеннона не означает, что количество информации в сообщении — отри­цательная величина. Объясняется это тем, что вероятность р, согласно определению, меньше едини­цы, но больше нуля. Так как логарифм числа, меньшего единицы, т.е. logp_i — величина отрицательная, то произведение вероятности на логарифм числа будет положительным.

ПОНЯТИЕ ЭНТРОПИИ В ТЕОРИИ ИНФОРМАЦИИ.

В результате развития теории информации и ее приложений идеи Шеннона быст­ро распространяли свое влияние на самые различные области знаний. Было замечено,

что формула Шеннона 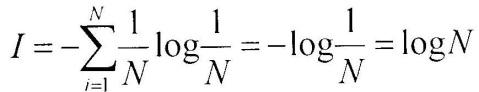очень похожа на используемую в фи­зике формулу энтропии, выведенную Больцманом.

Энтропия (информационная) – мера хаотичности информации, неопределённость появления какого-либо симовала первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на симовл передаваемого сообщения. Энтропия обозначает степень не­упорядоченности статистических форм движения молекул. Энтропия максимальна при равновероятном распределении параметров движения молекул (направлении, ско­рости и пространственном положении). Значение энтропии уменьшается, если дви­жение молекул упорядочить. По мере увеличения упорядоченности движения энтро­пия стремится к нулю (например, когда возможно только одно значение и направление скорости). При составлении какого-либо сообщения (текста) с помощью энтропии можно характеризовать степень неупорядоченности движения (чередования) симво­лов. Текст с максимальной энтропией — например: ИХЗЦЗЦЩУЩУШКШГЕНЕ-ЭФЖ.

Используя различие формул количества информации Шеннона и энтропии Больцмана (разные знаки), Л. Бриллюэн охарактеризовал информацию как отрица­тельную энтропию, или негэнтропию. Так как энтропия является мерой неупорядо­ченности, то информация может быть определена как мера упорядоченности матери­альных систем.

3. СЕМАНТИЧЕСКАЯ КОНЦЕПЦИЯ ИНФОРМАЦИИ. ПОНЯТИЕ ТЕЗАУРУСА. ЗАКОНОМЕРНОСТИ ВОСПРИЯТИЯ ИНФОРМАЦИИ РЕЦИПИЕНТОМ В РАМКАХ ТЕЗАУРУСНОЙ МОДЕЛИ КОММУНИКАЦИИ.

СЕМАНТИЧЕСКАЯ КОНЦЕПЦИЯ ИНФОРМАЦИИ.

Семантика изучает знаковые системы как средства выражения смысла, опреде­ленного содержания, т. е. правила интерпретации знаков и их сочетаний, смысловую сторону языка.

Основная идея семантической концепции информации заключается в возмож­ности измерения содержания (предметного значения) суждений. Но содержание все­гда связано с формой, поэтому синтаксические и семантические свойства информа­ции взаимосвязаны, хотя и различны. Получается, что содержание все-таки можно из­мерить через форму, т. е. семантические свойства информации выразить через синтак­сические. Поэтому и исследования семантики базировались на понятии информации как уменьшении или устранении неопределенности, с которым мы уже знакомы.

Сразу же заметим, что методы точного количественного определения смыслового содержания информации в настоящее время еще не разработаны, поэтому мы ограни­чимся только кратким описанием подходов к решению этой проблемы.

Первую попытку построения теории семантической информации предприняли Р. Карнап и И. Бар-Хиллел. Они предложили определять величину семантической ин­формации посредством так называемой логической вероятности, которая представ­ляет собой степень подтверждения той или иной гипотезы. Таким образом, семантико-информационное содержание высказывания определяется не тем, что содержит данное высказывание, а тем, что оно исключает.

Однако, несмотря на определенные достижения, концепция Карнапа — Бар-Хиллела оказалась малопригодной для анализа содержания естественного языка. Эта теория, основанная на вероятностной логике, неприменима к анализу основного мас­сива научного знания — достоверного знания. С точки зрения указанной теории, на­пример, высказывание «На Луне есть нефть» содержит информацию, а высказывание «На Земле есть нефть» лишено информации, поскольку это достоверное знание. Та­кая ситуация представлялась довольно парадоксальной!

Все здание человеческого знания, согласно этой модели, можно рассматривать в виде совокупности смысловыражающих элементов и смысловых отношений между ними. Множество смысловыражающих элементов и смысловых отношений на нем на­зывается тезаурусом. Слово «тезаурус» происходит от греческого — сокровище, со­кровищница, все огромное множество понятий и отношений между ними, иными сло­вами, тезаурус составляет главное сокровище человека — его знания. Таким обра­зом, ТЕЗАУРУС — это знание, представленное в виде понятий и отношений меж­ду ними, т. е. определенным образом структурированное знание.

В широком смысле Тезаурус интерпретируют как описание системы знаний о действительности, которыми располагает индивидуальный носитель информации или группа носителей. Этот носитель может выполнять функции приёмника дополнительной информации, вследствие чего изменяется и его Тезаурус. Исходный тезаурус определяет при этом возможность приёмника при получении им семантической информации. Тезаурус фактически содержит не только информацию о действительности, но и метаинформацию (сведения об информации), обеспечивающую возможность приёма новых сообщений.

ЗАКОНОМЕРНОСТИ ВОСПРИЯТИЯ ИНФОРМАЦИИ РЕЦИПИЕНТОМ В РАМКАХ ТЕЗАУРУСНОЙ МОДЕЛИ КОММУНИКАЦИИ.

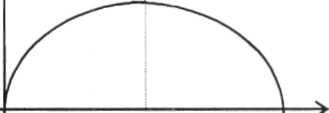
Обратимся в этой связи к модели семантической информации, в основе которой лежит понятие тезау­руса. Основы этой модели, состоят в следующем. Знания предлагается рассматривать в виде совокупности смысловыражающих элементов и смысловых связей между ними — тезауруса. Информация есть то, что воз­действуя на тезаурус, изменяет его. Отсутствие изменений в тезаурусе при получении сообщения означает отсутствие информации в сообщении — для данного реципиента. Зависимость информации, воспринимаемой получателем из сообщения, от величины тезауруса имеет примерно такой вид:

Приведенная зависимость, выражающая ключевую идею «тезаурусной» модели коммуникации, позво­ляет отметить важное обстоятельство: предварительное увеличение запаса знаний в тезаурусе («операция расширения тезауруса) может не только уменьшать, но и увеличивать величину информации, извлекаемой из сообщения. Эта особенность модели семантической теории информации существенно отличает ее от классиче­ской теории информации.

Понятие тезауруса в приведенной модели семантической информации не определено строго (понятия «смысловыражающий элемент», «смысл»>, однако его введение позволяет:

оперировать с новой единицей информации — понятием (смысловыражающим элементом, отношени­ем) как элементом тезауруса;

учитывать релятивность (сопоставление) семантической информации как функцию объемов тезаурусов источника и реципиента.

Принятие единицы семантической информации — понятия — делает заманчивым понятие энтропии. В этой связи обращает на себя внимание внешнее сходство представленной на рис.1 кривой с графиком энтро­пии для двух зависимых случайных событий.

В семантической модели информации вероятность появления того или иного понятия в сообщении -достаточно важная характеристика процесса коммуникации, но принципиальное значение имеет другое: из­вестно ли это понятие реципиенту информации, иными словами, содержится оно уже в его тезаурусе, или нет. По этому, основному для тезаурусной модели признаку множество понятий, составляющих сообщение, разбивается на два подмножества — известных и не известных реципиенту до коммуникации, и существенны именно вероятности появления понятий из этих подмножеств. Тогда коммуникация (в рамках семантической ее модели!) может рассматриваться как традиционный для теории информации опыт с двумя возможными исходами (появление известного или не известного реципиенту элемента), причем случайные события, соот­ветствующие этим исходам — зависимы. Это означает, что сумма вероятностей их появления равна единице.

Эту аналогию можно интерпретировать следующим образом. До коммуникации существует некоторое характерное именно для данной пары «источник — реципиент» соотношение известных и не известных реци­пиенту элементов источника. Математическим ожиданием этой вероятности и является энтропия. Энтропия максимальна при равновероятности появления известных или неизвестных элементов. Сопоставим теперь этот результат с зависимостью эффективности коммуникации от соотношения тезаурусов источника и ре­ципиента. Воспользовавшись тем, что в тезаурусной модели коммуникации фигурирует единица информации («элемент» тезауруса — понятие), можно сделать шаг к формализации этой зависимости, характеризуя относи­тельную «величину» тезаурусов, их «объем» вероятностями появления в них тех или иных элементов (поня­тий).

Прежде чем перейти к формальным рассуждениям, сделаем несколько замечаний, касающихся содержа­тельности самого понятия тезауруса Перейдем теперь к анализу тезаурусной модели коммуникации

В первом случае коммуникация невозможна в третьем — бессмысленна (информация источника уже имеется у реципиента). Полезная коммуникация соответствует второй из перечисленных ситуаций, когда тезаурусы источника и реципиента пересекаются (Рис. 2).

Что означает термин энтропия точки зрения теории информации

Окончание. Начало в №2, №3 2016

6. Энтропия Шеннона

Клод Шеннон первым начал интерпретировать передаваемые сообщения и шумы в каналах связи с точки зрения статистики, рассматривая как конечные, так и непрерывные множества сообщений. Клода Шеннона называют «отцом теории информации».

Одной из самых известных научных работ Клода Шеннона является его статья «Математическая теория связи», опубликованная в 1948 году.

В этой работе Шеннон, исследуя проблему рациональной передачи информации через зашумленный коммуникационный канал, предложил вероятностный подход к пониманию коммуникаций, создал первую, истинно математическую, теорию энтропии как меры случайности и ввёл меру дискретного распределения p вероятности на множестве альтернативных состояний передатчика и приёмника сообщений.

Шеннон задал требования к измерению энтропии и вывел формулу, ставшую основой количественной теории информации:

H (p).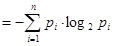

Здесь n – число символов, из которых может быть составлено сообщение (алфавит), H – информационная двоичная энтропия.

На практике значения вероятностей p_i в приведённой формуле заменяют их статистическими оценками: p_i 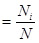– относительная частота i-го символа в сообщении, где N – число всех символов в сообщении, N_i – абсолютная частота i-го символа в сообщении, т.е. число встречаемости i-го символа в сообщении.

Во введении к своей статье «Математическая теория связи» Шеннон отмечает, что в этой статье он расширяет теорию связи, основные положения которой содержатся в важных работах Найквиста и Хартли.

Гарри Найквист (1889-1976) –
американский инженер шведского
происхождения, один из пионеров
теории информации

Первые результаты Найквиста по определению ширины частотного диапазона, требуемого для передачи информации, заложили основы для последующих успехов Клода Шеннона в разработке теории информации.

В 1928 году Хартли ввёл логарифмическую меру информации H = K · log₂N, которую часто называют хартлиевским количеством информации.

Хартли принадлежит следующая важная теорема о необходимом количестве информации: если в заданном множестве M, состоящем из N элементов, содержится элемент x, о котором известно только то, что он принадлежит этому множеству M, то, чтобы найти x, необходимо получить об этом множестве количество информации, равное log₂N бит.

Кстати, отметим, что название БИТ произошло от английской аббревиатуры BIT – BInary digiT. Этот термин впервые был предложен американским математиком Джоном Тьюки в 1946 году. Хартли и Шеннон использовали бит как единицу измерения информации.

Вообще, энтропия Шеннона – это энтропия множества вероятностей p₁, p₂,…, p_n.

Ральф Винтон Лайон Хартли (1888-1970)
– американский учёный-электронщик

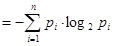
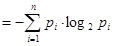
Строго говоря, если X – конечная дискретная случайная величина, а p₁, p₂,…, p_n – вероятности всех её возможных значений, то функция H (X ) задаёт энтропию этой случайной величины, при этом, хотя X и не является аргументом энтропии, можно записывать H (X ).

Аналогично, если Y – конечная дискретная случайная величина, а q₁, q₂,…, q_m – вероятности всех её возможных значений, то для этой случайной величины можно записывать H (Y ).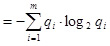

Джон Уайлдер Тьюки (1915-2000) –
американский математик. Тьюки избрал
бит для обозначения одного разряда
в двоичной системе счисления

Шеннон назвал функцию H(X )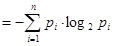энтропией по совету Джона фон Неймана.

Нейман убеждал: эту функцию следует назвать энтропией «по двум причинам. В первую очередь, Ваша функция неопределённости была использована в статистической механике под этим именем, так что у неё уже есть имя. На втором месте, и что более важно, никто не знает, что такое энтропия на самом деле, так что в дискуссии Вы всегда будете иметь преимущество».

Надо полагать, что этот совет Неймана не был простой шуткой. Скорее всего, и Джон фон Нейман и Клод Шеннон знали об информационной интерпретации энтропии Больцмана как о величине, характеризующей неполноту информации о системе.

В определении Шеннона энтропия – это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения.

7. Энтропия Колмогорова

А.Н. Колмогоровым были получены фундаментальные результаты во многих областях математики, в том числе в теории сложности алгоритмов и теории информации.

В частности, ему принадлежит ключевая роль в превращении теории информации, сформулированной Клодом Шенноном как технической дисциплины, в строгую математическую науку, и в построении теории информации на принципиально иной, отличной от шенноновской, основе.

В своих работах по теории информации и в области теории динамических систем А.Н. Колмогоров обобщил понятие энтропии на эргодические случайные процессы через предельное распределение вероятностей. Чтобы понять смысл этого обобщения, необходимо знать основные определения и понятия теории случайных процессов.

Значение энтропии Колмогорова (еще называемой K-энтропией) задает оценку скорости потери информации и может интерпретироваться как мера «памяти» системы, или мера скорости «забывания» начальных условий. Её можно также рассматривать как меру хаотичности системы.

8. Энтропия Реньи

Альфред Реньи ввёл однопараметрический спектр энтропий Реньи.

С одной стороны, энтропия Реньи представляет собой обобщение энтропии Шеннона. А с другой стороны, одновременно с этим она представляет собой обобщение расстояния (расхождения) Кульбака-Лейблера. Отметим также, что именно Реньи принадлежит полное доказательство теоремы Хартли о необходимом количестве информации.

Расстояние Кульбака-Лейблера (информационная дивергенция, относительная энтропия) – это несимметричная мера удалённости друг от друга двух вероятностных распределений.

Обычно одно из сравниваемых распределений является «истинным» распределением, а второе распределение – предполагаемым (проверяемым) распределением, являющимся приближением первого.

Пусть X, Y – это конечные дискретные случайные величины, для которых области возможных значений принадлежат заданному множеству и известны функции вероятности: P (X = a_i) = p_i и P (Y = a_i) = q_i.

Тогда значение DKL расстояния Кульбака-Лейблера вычисляется по формулам

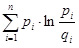
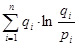
D_KL (X, Y ) =, D_KL (Y, X ) = .

В случае абсолютно непрерывных случайных величин X, Y, заданных своими плотностями распределения, в формулах для вычисления значения расстояния Кульбака-Лейблера суммы заменяются соответствующими интегралами.

Расстояние Кульбака-Лейблера всегда является неотрицательным числом, при этом оно равно нулю D_KL(X, Y) = 0 тогда и только тогда, когда для заданных случайных величин почти всюду справедливо равенство X = Y.

В 1960 году Альфред Реньи предлагает своё обобщение энтропии.

Энтропия Реньи представляет собой семейство функционалов для количественного разнообразия случайности системы. Реньи определил свою энтропию как момент порядка α меры ε-разбиения (покрытия).

Пусть α – заданное действительное число, удовлетворяющее требованиям α ≥ 0, α ≠ 1. Тогда энтропия Реньи порядка α определяется формулой H_α = H_α (X )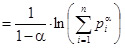, где p_i = P (X = x_i) – вероятность события, состоящего в том, что дискретная случайная величина X окажется равна своему соответствующему возможному значению, n – общее число различных возможных значений случайной величины X.

В противном случае, значения энтропий Реньи слабо уменьшаются при возрастании значений параметра α. Энтропии Реньи играют важную роль в экологии и статистике как индексы разнообразия.

Энтропия Реньи также важна в квантовой информации, она может быть использована в качестве меры сложности.

Рассмотрим некоторые частные случаи энтропии Реньи для конкретных значений порядка α:

1. Энтропия Хартли: H = H (X ) = ln n, где n – мощность области возможных значений конечной случайной величины X, т.е. количество различных элементов, принадлежащих множеству возможных значений;

2. Информационная энтропия Шеннона: H₁ = H₁ (X ) = H₁ (p) 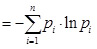(определяется как предел при α → 1, который несложно найти, например, с помощью правила Лопиталя);

3. Корреляционная энтропия или столкновение энтропии: H₂ = H₂ (X )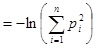= – ln ( X = Y );

4. Min-энтропия: H_∞ = H_∞(X ).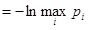

Альфред Реньи ввёл не только свои абсолютные энтропии (1.15), он определил также спектр мер расхождений, обобщающих расхождения Кульбака-Лейбнера.

Пусть α – заданное действительное число, удовлетворяющее требованиям α > 0, α ≠ 1. Тогда в обозначениях, использованных при определении значения D_KL расстояния Кульбака-Лейблера, значение расхождения Реньи порядка α определяется формулами

D_α(X, Y ), D_α(X, Y ).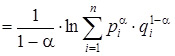

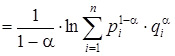
Расхождение Реньи также называют alpha-расхождением или α-дивергенцией. Сам Реньи использовал логарифм по основанию 2, но, как всегда, значение основания логарифма абсолютно неважно.

9. Энтропия Тсаллиса

В 1988 году Константино Тсаллис предложил новое обобщение энтропии, являющееся удобным для применения с целью разработки теории нелинейной термодинамики.

Предложенное им обобщение энтропии, возможно, в ближайшем будущем сможет сыграть существенную роль в теоретической физике и астрофизике.

Энтропия Тсаллиса Sq, часто называемая неэкстенсивной (неаддитивной) энтропией, определяется для n микросостояний согласно следующей формуле:

S_q = S_q (X ) = S_q (p) = K· , .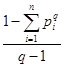

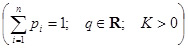
Здесь K – размерная константа, если размерность играет важную роль для понимания задачи.

Тсаллис и его сторонники предлагают развивать «неэкстенсивную статистическую механику и термодинамику» в качестве обобщения этих классических дисциплин на случай систем с длинной памятью и/или дальнодействующими силами.

От всех других разновидностей энтропии, в т.ч. и от энтропии Реньи, энтропия Тсаллиса отличается тем, что не является аддитивной. Это принципиальное и важное отличие.

Тсаллис и его сторонники считают, что эта особенность даёт возможность построить новую термодинамику и новую статистическую теорию, которые способы просто и корректно описывать системы с длинной памятью и системы, в которых каждый элемент взаимодействует не только с ближайшими соседями, но и со всей системой в целом или её крупными частями.

Примером таких систем, а поэтому и возможным объектом исследований с помощью новой теории, являются космические гравитирующих системы: звёздные скопления, туманности, галактики, скопления галактик и т.п.

Начиная с 1988 года, когда Константино Тсаллис предложил свою энтропию, появилось значительное число приложений термодинамики аномальных систем (с длиной памятью и/или с дальнодействующими силами), в том числе и в области термодинамики гравитирующих систем.

10. Квантовая энтропия фон Неймана

Энтропия фон Неймана играет важную роль в квантовой физике и в астрофизических исследованиях.

Джон фон Нейман внёс значительный вклад в развитие таких отраслей науки, как квантовая физика, квантовая логика, функциональный анализ, теория множеств, информатика и экономика.

Он являлся участником Манхэттенского проекта по разработке ядерного оружия, одним из создателей математической теории игр и концепции клеточных автоматов, а также основоположником современной архитектуры компьютеров.

Энтропия фон Неймана, как всякая энтропия, связана с информацией: в данном случае – с информацией о квантовой системе. И в этом плане она играет роль фундаментального параметра, количественно характеризующего состояние и направление эволюции квантовой системы.

В настоящее время энтропия фон Неймана широко используется в различных формах (условная энтропия, относительная энтропия и т.д.) в рамках квантовой теории информации.

Различные меры запутанности непосредственно связаны с энтропией фон Неймана. Тем не менее, в последнее время появился ряд работ, посвящённых критике энтропии Шеннона как меры информации и возможной её неадекватности, и, следовательно, неадекватности энтропии фон Неймана как обобщения энтропии Шеннона.

Проведенный обзор (к сожалению, беглый, а порой и недостаточно математически строгий) эволюции научных взглядов на понятие энтропии позволяет дать ответы на важные вопросы, связанные с истинной сущностью энтропии и перспективами применения энтропийного подхода в научных и практических исследованиях. Ограничимся рассмотрением ответов на два таких вопроса.

Первый вопрос: имеют ли между собой многочисленные разновидности энтропии, как рассмотренные, так и не рассмотренные выше, что-нибудь общее кроме одинакового названия?

Этот вопрос возникает естественным образом, если принять во внимание то разнообразие, которое характеризует существующие различные представления об энтропии.

На сегодня научное сообщество не выработало единого, признанного всеми, ответа на этот вопрос: одни учёные отвечают на этот вопрос утвердительно, другие – отрицательно, третьи – относятся к общности энтропий различных видов с заметной долей сомнения.

Клаузиус, по-видимому, был первым учёным, убеждённым в универсальном характере энтропии и полагавшим, что во всех процессах, происходящих во Вселенной, она играет важную роль, в частности, определяя их направление развития во времени.

Кстати, именно Рудольфу Клаузиусу принадлежит одна из формулировок второго начала термодинамики: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему».

Эту формулировку второго начала термодинамики называют постулатом Клаузиуса, а необратимый процесс, о котором идёт речь в этом постулате, – процессом Клаузиуса.

Со времени открытия второго начала термодинамики необратимые процессы играли уникальную роль в физической картине мира. Так, знаменитая статья 1849 года Уильяма Томпсона, в которой приведена одна из первых формулировок второго начала термодинамики, называлась «Об универсальной тенденции в природе к диссипации механической энергии».

Отметим также, что и Клаузиус был вынужден использовать космологический язык: «Энтропия Вселенной стремится к максимуму».

Илья Романович Пригожин (1917-2003) –
бельгийско-американский физик и
химик российского происхождения,
лауреат Нобелевской премии
по химии 1977 года

К аналогичным выводам пришёл Илья Пригожин. Пригожин полагает, что принцип энтропии ответственен за необратимость времени во Вселенной и, возможно, играет важную роль в понимании смысла времени как физического феномена.

К настоящему времени выполнено множество исследований и обобщений энтропии, в том числе и с точки зрения строгой математической теории. Однако заметная активность математиков в этой области пока не востребована в приложениях, за исключением, пожалуй, работ Колмогорова, Реньи и Тсаллиса.

Несомненно, энтропия – это всегда мера (степень) хаоса, беспорядка. Именно разнообразие проявления феномена хаотичности и беспорядка обусловливает неизбежность разнообразия модификаций энтропии.

Второй вопрос: можно ли признать сферу применения энтропийного подхода обширной или все приложения энтропии и второго начала термодинамики ограничиваются самой термодинамикой и смежными направлениями физической науки?

История научного изучения энтропии свидетельствует, что энтропия – это научное явление, открытое в термодинамике, а затем успешно перекочевавшее в другие науки и, прежде всего, в теорию информации.

Несомненно, энтропия играет важную роль практически во всех областях современного естествознания: в теплофизике, в статистической физике, в физической и химической кинетике, в биофизике, астрофизике, космологии и теории информации.

Говоря о прикладной математике, нельзя не упомянуть приложения принципа максимума энтропии.

Как уже отмечалось, важными областями применения энтропии являются квантово-механические и релятивистские объекты. В квантовой физике и астрофизике такие применения энтропии представляют собой большой интерес.

Упомянем лишь один оригинальный результат термодинамики чёрных дыр: энтропия чёрной дыры равна четверти площади её поверхности (площади горизонта событий).

В космологии считается, что энтропия Вселенной равна числу квантов реликтового излучения, приходящихся на один нуклон.

Таким образом, сфера применения энтропийного подхода весьма обширна и включает в себя самые разнообразные отрасли знания, начиная с термодинамики, других направлений физической науки, информатики и заканчивая, например, историей и экономикой.

А.В. Сигал , доктор экономических наук, Крымский университет имени В.И. Вернадского